基于Criminisi的结构组稀疏表示图像修复算法
2020-04-09唐贵进刘小花崔子冠
王 君,唐贵进,刘小花,崔子冠
(南京邮电大学 江苏省图像处理与图像通信重点实验室,江苏 南京 210003)
0 引 言
图像修复指根据图像的已有信息,按照一定规则对破损区域做出合理猜测并填充,从而使重构图像最大程度地接近原始图像。图像修复最早用于古画、雕塑等文物的复原工作[1],在图像信息技术蓬勃发展的今天,图像在下载、压缩、发送或存储的过程中都可能发生失真或破坏[2],因而图像修复变得尤为重要。
目前主流的图像修复算法主要分为三大类[3]:基于偏微分方程(partial differential equation,PDE)、基于纹理结构(texture synthesis)和基于稀疏表示(sparse representation)方法的图像修复。PDE模型本质上就是利用变分法求解能量泛函的极值,主要包括TV模型、BSCB模型和CDD模型[4-5]等算法,这类算法在处理大面积区域缺失图像时容易产生大面积模糊。Criminisi等人[6]提出,根据一定规则在图像已知区域寻找与缺失区域相匹配的图像块,该算法得到的修复结果纹理清晰,但对于纹理特征不够明显的破损图像,容易产生纹理延伸现象[7]。
基于稀疏表示理论的图像修复算法通过求解稀疏表示模型来实现图像的重构。传统的稀疏表示算法[8]通常独立考虑每个图像块,而Zhang J等人[9-10]提出的结构组稀疏表示算法(SGSR)提出了结构组的概念,考虑了图像块之间的联系,并且通过直接对结构组的估计值做奇异值分解得到学习字典,计算复杂度小鲁棒性高,但是,算法中采用双线性插值算法求解结构组的估计量,导致块状区域缺损图像的修复效果不好。文中借助Criminisi等人[6]提出的大区域缺损图像修复算法,对块状区域缺损图像的像素值进行更有效的预估,使得重构图像纹理更自然、结构更加清晰。
1 相关知识
1.1 构造结构组

图1 构造结构组
(1)
1.2 稀疏表示模型
同一幅图像中,已知信息区域和未知信息区域的稀疏性近似相同,所以可以用同一稀疏解表示[12]。稀疏矩阵α的稀疏性由L0范数衡量,信号x可以由字典D中的几个原子精确表示,如下式:
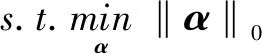
(2)
同理,为了得到结构组的稀疏表示模型,首先找到其对应的字典DGk,利用字典中尽量少的原子来稀疏表示结构组xGk,而求解稀疏表示模型的过程就是求解这个稀疏矩阵αGk,通过字典和稀疏矩阵得到稀疏表示模型[13]:
(3)

1.3 学习字典
传统的字典学习算法通常通过交替优化字典和稀疏表示系数求得,由该方法求得的字典适用于整幅图像,而不是针对某一个结构组。这样的做法不仅计算量大而且忽略了想要利用图像块之间相似性的初衷,所以采用双线性插值算法得到结构组xGk的估计量rGk,先对数据做网格化处理,再利用双线性插值算法求得缺失像素值的估计值。
再对估计矩阵rGk进行奇异值分解[14],可得:
(4)
其中,uGk⊗i、vGk⊗i分别表示矩阵UGk和VGk的列向量,ΣGk表示对角矩阵,γrGk⊗i表示主对角元素,于是,字典DGk的每个原子定义为:
(5)
其中,每个原子dGk⊗i大小都为BS×c,因此,结构组xGk对应的自适应学习字典DGk为:
DGk=[dGk⊗1,dGk⊗2,…,dGk⊗m]
(6)
算法只采用一次奇异值分解即可得到与结构组自适应的学习字典,求得学习字典后,仍用rGk取代xGk得到稀疏表示模型,再用凸优化问题的方法求解模型中非凸的L0范数,采用SBI算法进行迭代优化,得到最终的修复效果。
由上述可见,估计量rGk是否精确直接关系到学习字典和稀疏矩阵的求解,并对最终的修复质量产生影响。上述算法在求结构组xGk的估计量rGk时,直接采用双线性插值函数对其处理,双线性插值算法根据周围像素点求缺失像素值,块状区域中越靠中间位置的像素值越无法准确估计。所以文中采用基于样本块的Criminisi修复算法,基于图像块对缺失区域进行估计,由此得到与原结构组相似度更高的估计量。
2 文中算法
2.1 算法描述
采用基于样本块的Criminisi算法得到结构组的估计值,首先要计算整幅图像的近似值。如图2所示,φ是缺失区域,通过掩模图像找到缺失区域边界δφ,任取边界上一像素点p,以点p为中心,得到图像块ψp,该图像块的置信项C(p)和数据项D(p)分别定义为:
(7)
(8)

图2 基于Criminisi的修复算法
其中,|Ψp|为图像块Ψp的像素点总数,为p点的等照度线方向,np为p点的法向量,α为归一化因子。由于置信度随着迭代次数增加会急剧趋近0,数据项在等照度线和法向量垂直时也为0,为了防止这两种情况一项发生就使得优先权为0,把图像块Ψp的优先权P(p)定义为:
P(p)=αC(p)+βD(p) s.t.α+β=1
(9)
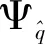
(10)
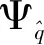
2.2 算法流程
得到整幅图像的估计值后,利用上节描述的构造组的方法对整幅图像的估计值进行计算,得到n个结构组的估计值后即可由估计值计算对应结构组的学习字典。基于结构组稀疏表示的优化算法流程如下:
输入:图像X,掩模图像M
初始化:t=0,k=0,n,迭代次数N
Whileφ!=0 do
计算C(p)和D(p)边缘优先权
取优先权最大的为待估计块
由欧氏距离得到最优匹配块
填充
End while
Whilek≤ndo
搜索c个xk的相似块得到结构组xGk,
End while
Whilet≤ndo
For eachxGk
根据式(4)~式(6)构建学习字典DGk

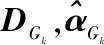
End for
End while
2.3 算法性能分析
针对文字掩模和块状掩模的去除,对文中算法收敛性进行的分析如图3所示。曲线以陡峭坡度上升到一定高度趋近平稳,说明图像质量先是有明显改善再逐渐趋于收敛。对于文字掩模和块状掩模的去除分别只需要进行20次迭代就趋于收敛,这是由于文中算法基于图像块来构造组,提高了修复效率。且在字典学习时相同结构组中的所有块采用同一字典的相同原子进行稀疏表示,只需要一次奇异值分解得到自适应字典,这也使得算法相较于K奇异值分解算法不仅高效、鲁棒,而且计算复杂度大大降低。
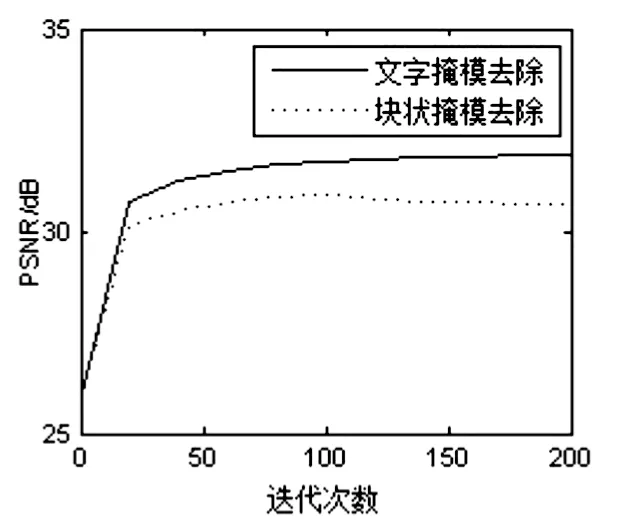
图3 峰值信噪比趋势变化
3 实验结果与分析
本节对文中算法的有效性进行验证,并做了大量测试实验,部分测试图片如图4所示。分别给图像添加文字掩模和块状区域掩模作为待修补图像输入,并将输出的实验结果与文献[3,15-16]的算法和SGSR算法进行对比。实验在戴尔Inspiron 14-7472笔记本上的MatlabR2014a上运行,该笔记本CPU为Intel酷睿i7 8550U,主频1.8 GHz,内存为8 GB,系统是Microsoft Windows 8。

图4 测试图片
除了主观视觉,还采用峰值信噪比(PSNR)和结构相似性(SSIM)作为客观评价标准,两项指标的公式描述如下:

(11)
SSIM(x,y)=l(x,y)c(x,y)s(x,y)
(12)
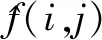
文中对大量图片做了测试后,在表1和表2中罗列了对十幅图像测试的客观指标参数,下面主要展示图像Flower和图像House的主观修复效果。

图5 文字去除
如图5所示,图(a)以文字图像作为掩模得到文字遮挡图像,由图5(b)-(f)可见,主观视觉上,SGSR算法和提出的优化算法明显优于文献[3,15-16]的算法。这一点在图片左下方窗户上以及树中的细小叶子中可以明显看出,文中算法得到的效果纹理清晰且结构上非常准确。客观评价上,文中算法比SGSR算法的PSNR评价指标提高了0.25 dB,SSIM评价指标提高了0.003。
如图6所示,图(a)是以块状区域做掩模图像得到的,主观视觉上,文献[15]算法和SGSR算法出现了大面积的模糊现象,而文献[16]和文献[3]的算法纹理较为清晰,但是结构上仍不是很准确,而文中算法得到的效果在结构上非常清晰。另外客观评价上,文中算法的PSNR评价指标比SGSR算法提高了9.38 dB,SSIM评价指标提高了0.006 3。

图6 块状区域修复
结合表1、表2的数据可以看出,相较于文献[3,15-16]以及SGSR算法,对各图像添加文字掩模时,文中算法的PSNR评价指标分别平均提高了7.88 dB、4.88 dB、7.61 dB、0.19 dB,SSIM评价指标分别提高了0.071 6、0.025 9、0.056 4、0.001 5,给各图像添加块状掩模时,文中算法PSNR评价指标分别平均提高了5.22 dB、10.19 dB、5.19 dB、2.66 dB,SSIM评价指标分别提高了0.009 6、0.013 2、0.011 2、0.001 7。综上所述,对于块状区域缺损图像,文中算法较SGSR算法的优化幅度更大,这是由于Criminisi算法可以比双线性插值算法更准确地估计缺失区域的像素值,所以得到的修复结果图纹理自然结构清晰。
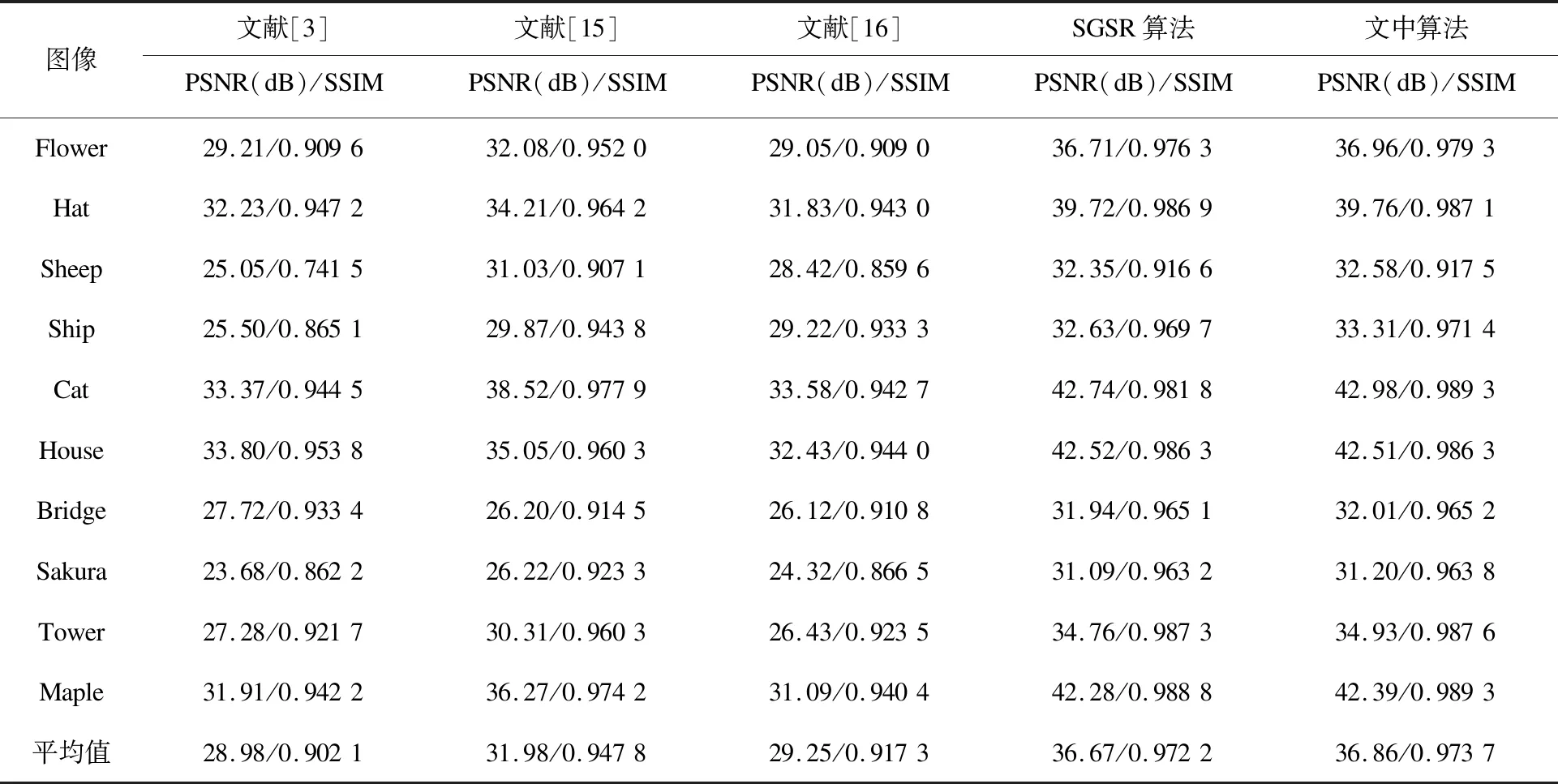
表1 各算法文字掩模去除结果对比
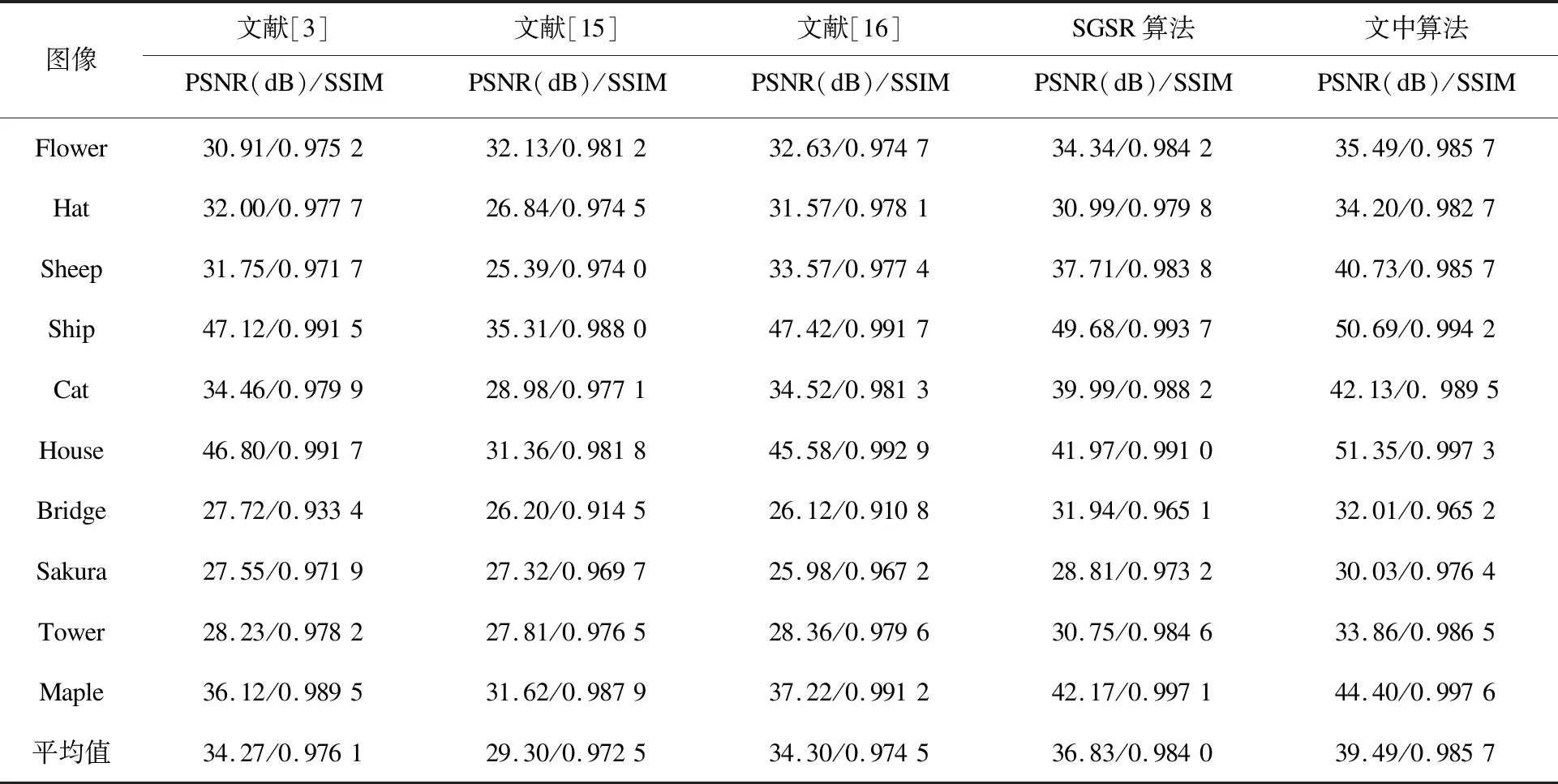
表2 各算法块状区域掩模去除结果对比
4 结束语
利用大区域修复算法计算缺失区域的估计值,该算法基于图像块进行估计而不是像素点,能够更加准确地估计缺失区域的像素值。接下来,对估计值进行奇异值分解得到与结构组自适应的学习字典,再借助字典和稀疏解得到修复图像。该算法具有高效性和鲁棒性。实验结果表明,该算法在主观视觉上纹理自然结构清晰,在峰值信噪比和结构相似性等客观标准下也得到了相应的提高。接下来的工作,会继续对该算法进行改进,使得算法能够适应更大面积的块状区域缺陷,且修复结果有连续的结构和自然的纹理。
