基于SAGBA优化粒子滤波的目标跟踪

闾斯瑶，周武能，李龙龙

(东华大学 信息科学与技术学院，上海 201620)

0 引 言

视觉目标跟踪的应用范围很广，涵盖了很多领域，诸如视频监控[1]、人机交互[2-3]、自动车辆控制[4]和人类行为分析[5]等任务都从视觉系统中受益，并大量利用目标跟踪。粒子滤波器普遍在视频目标跟踪应用[6-9]。粒子滤波器精度靠近最优估计，对于非线性和非高斯时变系统的状态估计求解比较适用。然而，标准粒子滤波(PF)会因解决权值退化的问题，发生样本贫化问题。针对PF样本贫化问题，文献[10]的算法可以增加粒子的多样性。文献[11]的算法选取的重采样方法会依据系统进行选择，使粒子更逼近于真实状态。然而，上述文献是通过重采样方法来改进算法，不能从源头处理粒子贫化。

基于群智能优化算法的粒子滤波[12]是一种较好的研究方向。因为群智能算法主要是在迭代和优化粒子群的分布状态方面来进行优化[13-14]，这不牵涉到直接抛弃较低权重的粒子，因而粒子可以在源头上解决粒子贫化问题。

蝙蝠算法(BA)[15]实现智能优化的方法是模仿真实世界的蝙蝠对食物进行捕捉行为。蝙蝠算法是一种类似粒子群算法基于搜寻的随机策略来找到最佳的算法。蝙蝠算法在随机性方面相较于其他算法具有一定的优势。文献[15]表明蝙蝠算法的综合性能更加强于目前的主流群智能优化算法，例如粒子群优化算法以及蚁群算法等。在文献[16]中发现，将蝙蝠算法与PF相结合后粒子滤波器的性能得到了进一步的增强。

但是，蝙蝠算法也有下述缺陷：后期收敛慢，较低的收敛精度，容易陷入局部最优等。文中算法是在蝙蝠算法中融合模拟退火和高斯扰动来优化粒子滤波(SAGBA-PF)，要优化的集合群体通过使用高斯扰动的变异操作进一步调节，这样能够增强全局寻优以及局部寻优能力。模拟退火算法具备在搜寻过程中的概率突变特点，而且能够避免在寻优过程中选取局部最优。它不仅在退火过程中获得了良好的解决方案，并且还会有一定的几率接收到相对较差的解决方案，该几率由温度参数控制，几率的值会随着温度的下降而减小。文中实验结果也证明SAGBA效果更佳。

1 基本粒子滤波算法

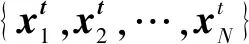
(1)

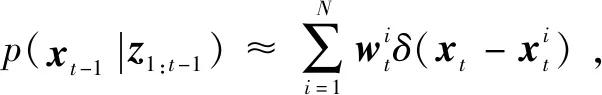
2 SAGBA-PF算法设计

为了确保粒子滤波器的准确性,文中算法目标函数如下:

(2)

2.1 SAGBA-PF全局搜索最优过程

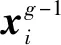
fi=fmin+(fmax-fmin)β

(3)

(4)

(5)

其中，β∈[0,1]服从均匀分布，x*是当前最优，fmin和fmax取决于ROI大小。

2.2 SAGBA-PF局部搜索最优过程

一旦获得局部最优，就使用随机游走模型生成蝙蝠个体新解，文中算法中的局部搜索方法为：

若rand>ri，则

xnew=xold+εAg

(6)

(7)

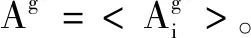
得到蝙蝠个体相对应的适应度值，并更新每个蝙蝠个体的相对更优位置，在上述相对更优位置处使用式(8)进行高斯扰动操作，然后比较高斯扰动之前和之后的位置以找出最优的位置和相对应的最优值xpbest；

xt=xt+a⊕ε

(8)

2.3 SAGBA-PF全局和局部搜索寻优调整过程

响度Ai和脉冲率ri的更新意义在于如果找到或者接近目标，蝙蝠个体会在降低响度的同时增加脉冲率，其计算方法如下：

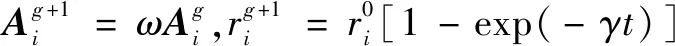
(9)

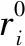
对于任何0<ω和γ<1，有：

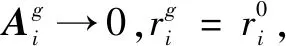
(10)

3 文中算法流程

文中算法流程如图1所示。可以看到整个蝙蝠种群中，可以使得各个蝙蝠个体避免陷于局部最优，避免了个体状态值在迭代过程，变化不大的情况。可以看到该算法可以使得粒子的多样性增加，进而提高粒子样本的质量。

4 仿真实验和结果分析

在仿真实验中，选取的过程模型和观测模型如下：

过程模型：

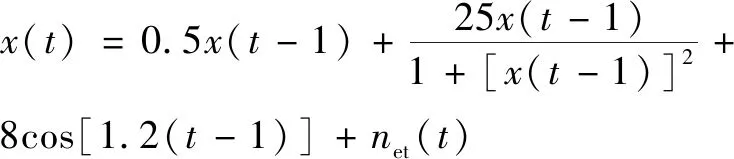
(11)

观测模型：

(12)

上述等式中，net(t)和wet(t)均是高斯噪声，平均值为零。

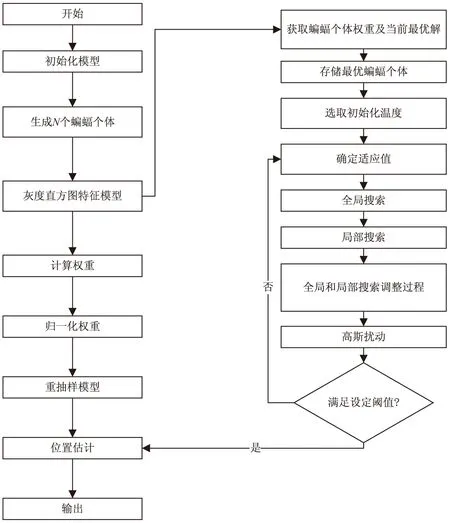
图1 算法流程

在仿真实验中，假设系统噪声方差分别为Q=1和Q=10，观测噪声方差R=10，滤波时间步长为50，初始化脉冲响度A0=0.5，初始化脉冲率r0=0.5，fmax=2，fmin=0，使用PF、PSO-PF和SAGBA-PF进行状态估计和跟踪该非线性系统。

在模拟退火算法部分中，文中算法设置的初始温度为TW0=1 000 °C，平衡温度TWmin=50 °C，最大迭代次数是20，退火方式如式(13)所示，退化系数as=0.99：

T=T*as

(13)

在文中算法中所使用的均方根误差公式为：

(14)

(1)当N=20、Q=10时，滤波状态误差如图2所示；

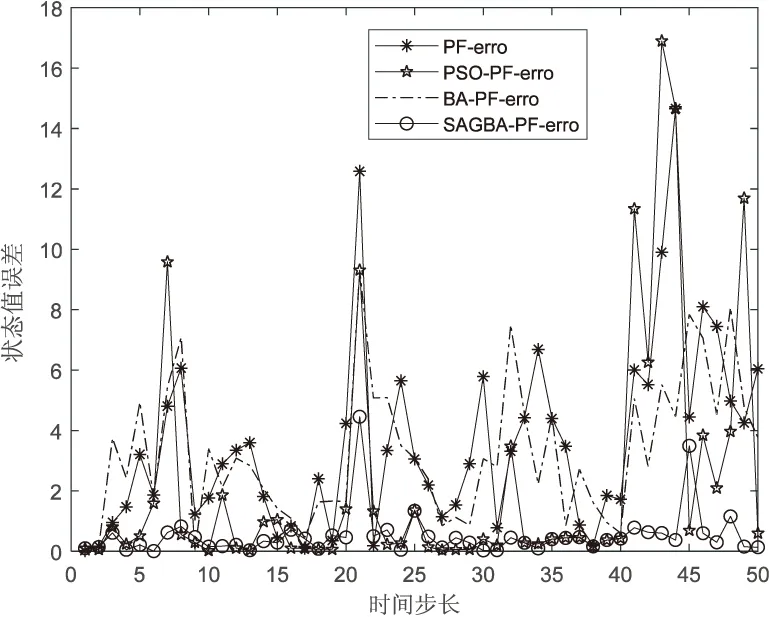
图2 N=20、Q=10时滤波状态误差绝对值

(2)当N=50、Q=10时，滤波状态误差如图3所示；

(3)当N=100、Q=10时，滤波状态误差如图4所示；

(4)当N=20、Q=1时，滤波状态误差如图5所示；

(5)当N=50、Q=1时，滤波状态误差如图6所示；

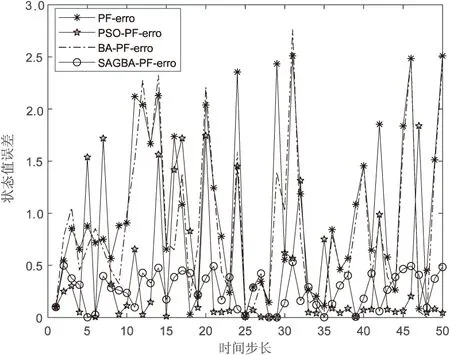
图6 N=50、Q=1时滤波状态误差绝对值

(6)当N=100、Q=1时，滤波状态误差如图7所示。

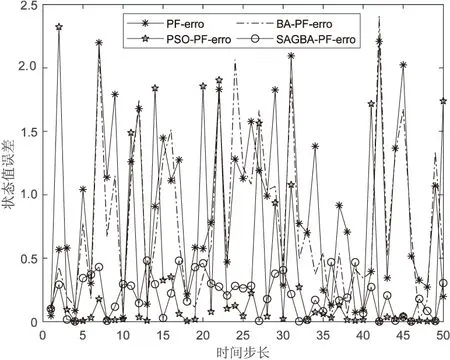
图7 N=100、Q=1时滤波状态误差绝对值

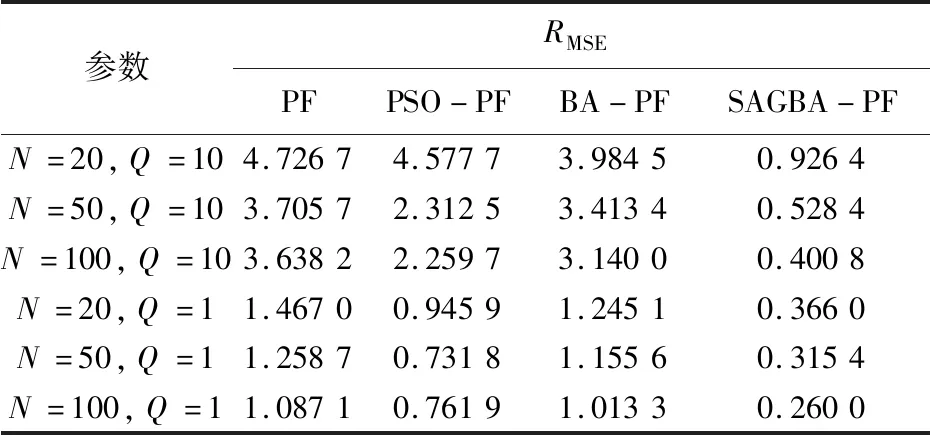
参数RMSEPFPSO-PFBA-PFSAGBA-PFN=20,Q=104.72674.57773.98450.9264N=50,Q=103.70572.31253.41340.5284N=100,Q=103.63822.25973.14000.4008N=20,Q=11.46700.94591.24510.3660N=50,Q=11.25870.73181.15560.3154N=100,Q=11.08710.76191.01330.2600

从图2～图7可以看出，相较于对比的几种算法，SAGBA-PF具有更好的状态值预测精度，因为融合模拟退火算法，对部分蝙蝠个体产生高斯扰动操作，执行进一步的搜索行为以存储蝙蝠个体相对更优值。随着进化过程的推进，模拟退火的温度逐渐降低，渐渐减少接受较差解的概率，从而提高算法的性能。该算法能够较大提高算法的收敛速度、鲁棒性和寻优能力。

从表1可以看出，在高噪声的影响下，当SAGBA-PF的蝙蝠个数为20时的精度依然高于PF中粒子数为100时的精度，这表明算法SAGBA-PF在非线性、高噪声的环境会较PF更好地跟踪目标。

5 结束语

文中提出的SAGBA-PF目标跟踪算法，全局搜索和局部搜索过程能力相对较好，提高了跟踪算法的跟踪性能。仿真结果表明，该算法具有较好的状态值预测精度。在后面的工作中，将对跟踪过程中的模板更新、目标遮挡等问题做进一步优化。