基于体素和三周期极小曲面的骨支架多孔结构设计
2020-04-08张壮雅李跃松段明德
张壮雅,赵 珂,李跃松,段明德
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.河南科技大学第一附属医院 影像科,河南 洛阳 471003)
0 引言
多孔结构作为表达模型内部结构的一种形式,具有较大的比表面积、较高的强度质量比,在特定的组织规则下能够表现出优良的渗透性和吸附性,在化工、组织工程、航空航天等领域都具有重要的应用价值[1-2]。其中在组织工程领域,骨支架是骨缺损组织修复和重建的重要载体[3-4],其设计要求除了在宏观结构方面与患者自体骨表面轮廓相一致外,在微观结构方面,也要求支架具有为种子细胞的黏附、繁殖、营养获取和新陈代谢提供生存空间及通道的微观多孔结构[5]。
传统组织工程骨支架制备的工艺,主要有粒子相分离法、静电纺丝法和气体发泡法等[6-8],虽然上述工艺方法能制造出内部孔隙结构呈连续的组织工程支架,但无法对支架内部孔隙结构、形状进行精确控制,难以制造出具有几何结构梯度和材料梯度的组织工程骨支架。近年来,增材制造(Additive Manufacturing, AM)技术的出现与日益成熟,为解决上述问题提供了可能,AM技术通过计算机辅助设计,采用逐层堆积成形的方法,在制造出与骨缺损部位相符宏观结构的同时,又能精确控制其复杂的微观多孔结构,因此AM技术的出现将组织工程支架的发展提到了一个新的高度[9]。但由于自然骨组织微观多孔结构的孔隙率、孔径大小以及孔隙分布等的复杂性和不规则性,难以对其进行有效的数学描述。因此,研究和设计性能良好的骨支架微观多孔结构,并能对其结构参数进行控制,对修复和重建大面积骨缺组织的临床治疗具有重要意义。
近年来,国内外学者围绕多孔结构设计方面做了大量的研究工作,尤飞等[10]提出一种基于多约束背包问题模型的骨支架建模方法,以椭球体作为构建多孔结构的基本孔隙单元,将支架的最小包围盒作为约束空间,利用混合遗传算法求解,构建了微观孔隙负模型,再通过与骨组织实体模型布尔运算,构建出含有微观多孔结构的实体支架模型;姚远等[11]提出基于体结构的装配设计方法,以球体作为构建微观孔隙的基础孔隙单元,通过局部区域优化,构建了密度、孔隙率和分布可控的复杂结构支架;与上述方法类似,Chantarapanich等[12]以阿基米德多面体及正多面体为基本孔隙单元,构建多孔支架模型,为提高设计效率,开发了多面体模型库,以适应特定支架微观孔隙的要求。从近年的研究可以看出,目前的骨支架建模方法主要基于CAD方法,以相对简单的球体、椭球体、圆柱体、棱柱、多面体等作为基本造孔单元来构建骨支架内部的多孔结构,近年的研究已取得了不少成果,为骨支架多孔结构设计提供了强大工具,但由于孔隙单元形状的局限,所设计的多孔结构缺乏多样性,在设计梯度孔隙结构时,常会在相邻单元接触面处出现边界融合问题。因此,在同一组织内部,仍难以实现孔隙形状、孔隙率、孔径大小及分布的梯度变化。
自然界中的蝴蝶羽翼、象鼻虫、甲壳类动物等,都是具有类似三周期极小曲面(Triply Periodic Minimal Surfaces, TPMS)的骨骼结构[13],TPMS因其在三维空间中3个独立方向均呈周期性的极小曲面,具有几何形状多样、可构建参数化数学模型等优点,而被国内外研究者重视。Rajagopalan等[14]首次提出了基于TPMS的组织支架设计方法,并以P单元为基本孔隙单元,构建了多孔支架模型,利用AM技术对其进行了制备;Almeida等[15]以Schwarz单元和Schoen单元为基本孔隙单元,采用Solidworks软件构造了两种单元的实体模型,通过等距偏移和加厚,分别研究了表面半径和厚度参数对支架孔隙率和机械性能的影响;Melchels等[16]基于G单元和D单元,构建了两种多孔单元支架模型,并利用AM技术对其进行了制备,与传统盐浸制备支架相比,其渗透率提高了近10倍,具有较好的互通性。
以上研究主要采用单一TPMS单元结构进行建模,针对梯度结构多孔设计的建模,也有学者进行了探索。Yoo等[17]采用体积距离场(Volumemetric Distance Field, VDF)和贝塔生长函数(Beta Growth Function, BGF)方法融合构建出结构更为复杂的TPMS单元,以此为基础,给定过渡边界,针对规则几何体进行了梯度结构多孔建模尝试。与该方法类似,Yang等[18]则基于径向基函数的融合方法,对梯度结构孔隙设计方法进行了研究,并采用mathematic软件进行了验证;王庆辉等[19]以单一的P单元为基本孔隙单元,进行了梯度孔隙研究,采用八叉树算法和Dual Contouring算法对骨骼实体模型进行了六面体网格划分,利用等参变化技术构建非封闭的骨支架多孔模型,并通过对六面体网格顶点编码、计算个体适应度等遗传操作,对网格大小及分布进行调节,进而实现对孔隙单元大小及分布的控制,构建出非封闭的骨支架多孔模型,最后再利用逆向工程软件Geomagic studio对其进行封闭。目前的研究取得了一定成果,但上述方法在孔隙形状、孔隙率以及孔径大小及分布的调节上缺乏灵活性,仍难以对其局部进行控制,基于TPMS的骨支架设计方法研究仍处于起步阶段。
基于此,本文提出一种基于三周期极小曲面和体素化的多孔骨支架的设计方法,采用隐函数表达的TPMS作为构建微观多孔结构的基本孔隙单元,通过定义距离函数和Log-Sigmoid函数,构建不同结构形式的TPMS单元三角网格模型;采用逆向几何求交体素化算法,对骨骼三角网格模型对象进行空间单元划分,从宏观上控制填充结构密度分布,确定目标装配区域;基于形函数坐标变换,构建出空间域多孔结构,通过布尔运算得到具有多孔结构的骨支架模型。
1 基于TPMS的孔隙单元设计
为阐述基于TPMS的孔隙单元设计方法,从TPMS曲面表达、不同TPMS过渡以及封闭TPMS单元构建等方面进行简要介绍。
(1)TPMS的隐式曲面表达
TPMS是一种在三维空间中三个独立方向均呈周期性的极小曲面(曲面上任意点的平均曲率为零),通常采用隐式曲面对其表达[20]:
(1)
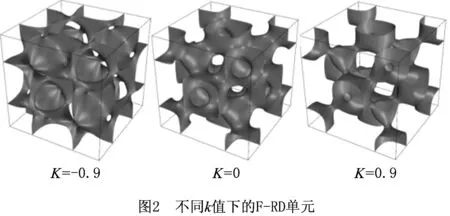
式中:Ak为幅度因子;k为周期波长;r为欧式空间的位置矢量;hk为倒数空间中第k个栅格矢量;Pk为相位偏移。当φ(r)=0时所定义的曲面即为TPMS。见的TMPS,有P曲面、G曲面和F-RD曲面,其表达式如下:
P:φp(x,y,z)=cos(x)+cos(y)+cos(z);
G:φG(x,y,z)=sin(x)cos(y)+sin(z)·
cos(x)+sin(y)cos(z)=0;
F-RD:φF-RD(x,y,z)=4cos(x)cos(y)cos(z)-
[cos(2x)cos(2y)+cos(2x)cos(2z)+
cos(2y)cos(2z)]=0。
(2)
通过引入距离函数k,可控制隐函数φTPMS(x,y,z,k)上点到φTPMS(x,y,z)的距离,改变TPMS形状[21]。
φTPMS(x,y,z,k)=φTPMS(x,y,z)+k=0。
(3)
图1和图2为不同k值下的P和F-RD单元。

(2)不同结构TPMS单元过渡
对于不同结构形式TPMS单元,通过权重系数α实现TPMS间的平滑过渡,即
φTPMS(x,y,z,α,k1,k2)=α(x,y,z)φ1(x,y,z,k1)+
(1-α(x,y,z))φ2(x,y,z,k2)=0。
(4)
式中α(x,y,z)∈(0,1),本文引入Log-Sigmoid函数作为其权重系数,其输出范围为(0,1)。
(5)
式中G(x,y,z)=0为TPMS单元间过渡边界。
以P,F-RD和G单元过渡为例,其表达式为:
(6)
其过渡模型如图3所示,其中:k1=-0.7,k2=0,k3=-0.9,G1(x,y,z)=x-5π,G2(x,y,z)=x+π。
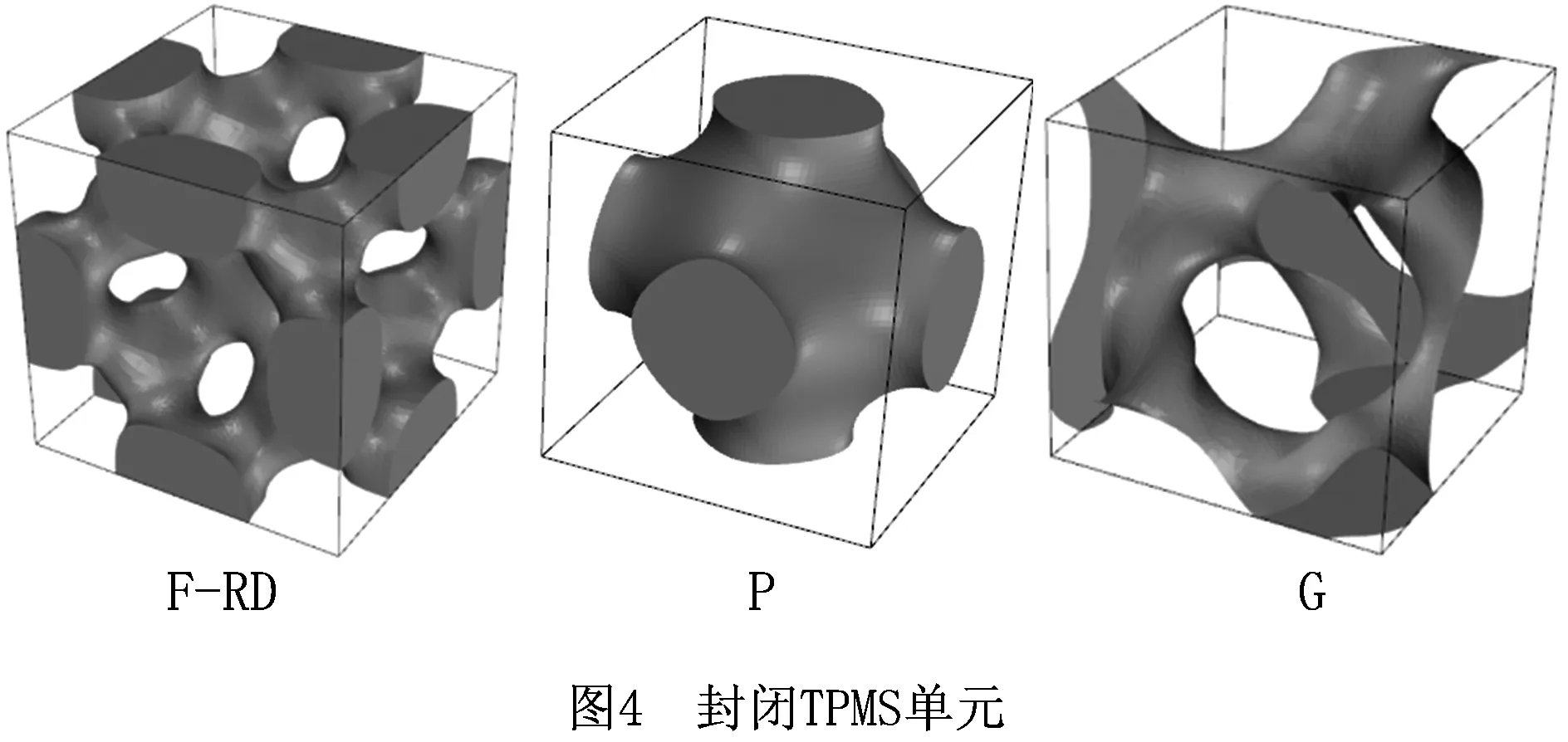
(3)封闭TPMS单元构建
由隐式表达的TPMS为非封闭隐式曲面,采用代数法,通过对TPMS与垂直于坐标轴平面求交构建封闭曲面单元,即
(7)
所构建的封闭F-RD、P和G单元如图4所示。

2 空间划分
对空间进行划分的目的是为所设计的孔隙单元提供装配空间区域。为提高计算效率,本文提出一种逆向几何求交的体素化方法对模型进行空间划分,即通过截面轮廓求取、等距扫描线填充、离散、立方体素填充,来构建骨支架体素化模型。
2.1 逆向几何求交计算截交线段
传统分层算法主要有基于模型毗邻关系的分层算法[22]和三角面片几何特征分类的分层算法[23],通过搜索三角网格模型中的三角面片,寻找与分层面存在交点的三角面片来求取截交线段,该类算法均难以避免三角面片与分层平面位置关系无效判断的情况。因此,本文提出逆向追踪求交的分层思路,以三角面片为基础,用三角面片坐标去搜索能与之产生交点的分层面,以此计算截交线段,其算法流程如下:
(1)分层面求取
首先遍历所有三角面片顶点坐标,得到模型的最大边界点(xmax,ymax,zmax)和最小边界点(xmin,ymin,zmin),建立模型的最小包围盒,即获得模型的分层范围。然后给定分层方向和分层间距,来建立分层面。以Z向为例,设分层间距为h,则建立的分层面坐标si为
(8)
为便于搜寻计算,将分层面坐标表达为一种类似散列表的数据结构。
(2)截交线段求取
在包围盒中按照一定的顺序选取三角面片,然后用三角面片坐标去搜索能与之相交的分层面,最后计算截交线段。对于任意三角面片m,与之相交的si,可通过式(9)判断:
(9)
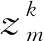
若三角面片m与si存在交点,则需要满足式(10)。散列表中si的索引值i可通过式(11)定位。
(10)
(11)
对于存在的大三角面片情况(即三角面片可能被多个分层面切割到),此时可由式(11)求得第一个i值后,进行i++运算,并通过式(10)判断,直到不满足条件为止。
截交线段求取可采用式(12)计算:
(12)
求得所有截面轮廓线段集合{L1,L2,…,Ln},这些线段集合必然构成若干个封闭的平行于Z平面的多边形,由于后续还需对求得的二维多边形进行等距扫描线离散、填充,因此无需对截面轮廓线段集合{L1,L2,…,Ln}进行顺序排列处理。
2.2 三维网格模型体素化
对分层后得到的截面轮廓线段进行等间距扫描线离散、填充生成体素化模型,以三维数组的结构形式表示,数组的维度为(L,W,H),L、W、H分别表示体素化模型长、宽、高各边上体素的个数,若数组内元素为0,表示没有体素占据,若为1,则表示有体素占据。
(13)
(1)扫描线求取
对分层后得到的截面轮廓线段,沿Y方向进行等间距扫描线填充,扫描间距为分层间距h,扫描线yi可通过式(14)确定,采用离散列表数据结构存储。
(14)
(2)扫描线与截面轮廓线段交点计算
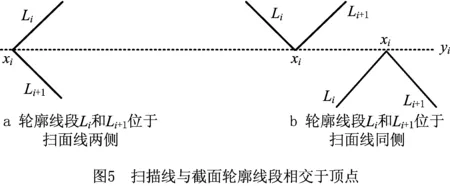
若yi与截面轮廓线段Li相交,则满足yimin≤yi≤yimax,其中(xi1,yi1),(xi2,yi2)为Li的两顶点坐标,yimin=min(yi1,yi2),yimax=max(yi1,yi2)。若截面轮廓线段Li与扫描线yi相交,则有以下3种情况:
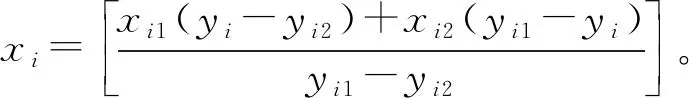
2)当yi=yimin
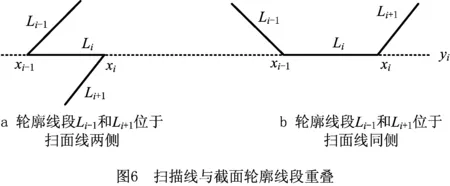
3)当yi=yimin=yimax时,截交线段与扫描线重合,如图6所示。若Li-1与Li+1分别位于扫描线yi两侧,此时认为扫描线与截面线段Li有一个交点(xi-1点),如图6a所示;若Li-1与Li+1位于扫描线y同侧,如图6b所示,此时记该截交线段的两个端点均为交点(xi-1点和xi点)。
(3)扫描线段求取
对(2)中求取的交点,按照X向坐标值从小到大顺序排列,判断其交点类型,并两两配对,从而得到一系列进出点,连接进出点即为所求取的扫描线段。
(4)扫描线段离散
对扫描线段沿着X方向进行等间距离散化,得到扫描线段离散二维点阵,离散距离为h,方法与前述类似,不再赘述。
(5)体素填充
所有的截面离散二维点阵,按分层方向组合,就构成了空间三维的均匀密度点阵。以点阵中的每个点坐标(xv,,yv,zv)为中心,填充边长为h的立方体,构成了体素化模型V。体素单元(m,n,k)的索引可通过式(15)计算:
(15)
3 微观孔隙单元装配及结构评价
3.1 基于等参变换的微观孔隙单元装配
微观孔隙单元装配,是将设计的微观孔隙单元按照一定的装配规则进行单元填充。为适应装配空间位置及尺寸变化,采用等参变换的方法[24],通过形函数坐标变换,将构建的TPMS孔隙单元装配(映射)到体素所划分的空间单元中。
为方便对不同尺寸的空间单元进行映射,通过式(16)构建标准孔隙单元。
(16)
式中:[x,y,z]为原孔隙单元控制六面体节点坐标,[xs,ys,zs]为转换后的标准孔隙单元控制六面体节点坐标,转换后的控制六面体和标准孔隙单元在x,y,z方向边界均为[-1,1]。
采用插值函数进行坐标变换
(17)
i=1,2,…,8。
(18)
式中:xi,yi,zi为体素化所构建的六面体网格节点笛卡尔坐标,可通过式(15)索引求取;x,y,z为六面体网格内部点笛卡尔坐标;ξi,ηi,ζi为自然坐标系下标准孔隙单元控制六面体节点坐标,对应式(16)中的点[xs,ys,zs];ξ,η,ζ为自然坐标系下标准单元内部点坐标,-1<ξ<1,-1<η<1,-1<ζ<1。
为获取整个组织工程支架内部孔隙模型,须将映射后的孔隙单元进行布尔并运算,从而得到整个组织工程支架微观孔隙负模型,即
φmicro_TPMS=φ1∪φ2∪…∪φi…∪φn。
(19)
式中:φi是第i个孔隙单元,φmicro_TPMS是整个骨组织微观孔隙负模型。
将得到的微观孔隙负模型与宏观外形结构的骨组织三角网格模型进行布尔差运算,得到宏微观结构的骨支架模型,即
φ3D_scaffold=φexterior_geometry∩φmicro_TPMS。
(20)
式中:φexterrior_geometry是宏观外形结构的骨组织三角网格模型,φ3D_scafford是宏微观结构的骨支架模型。
3.2 微观孔隙结构评价
组织工程骨支架内部微观结构,在种子细胞成骨阶段起着决定性作用,因此组织工程骨支架模型构建以后,须对其孔隙率、孔隙尺寸等指标进行评价。
(1)孔隙率
利用本文第2章中提出的体素化方法,对孔隙率近似计算,P单元的体素化如图7所示。
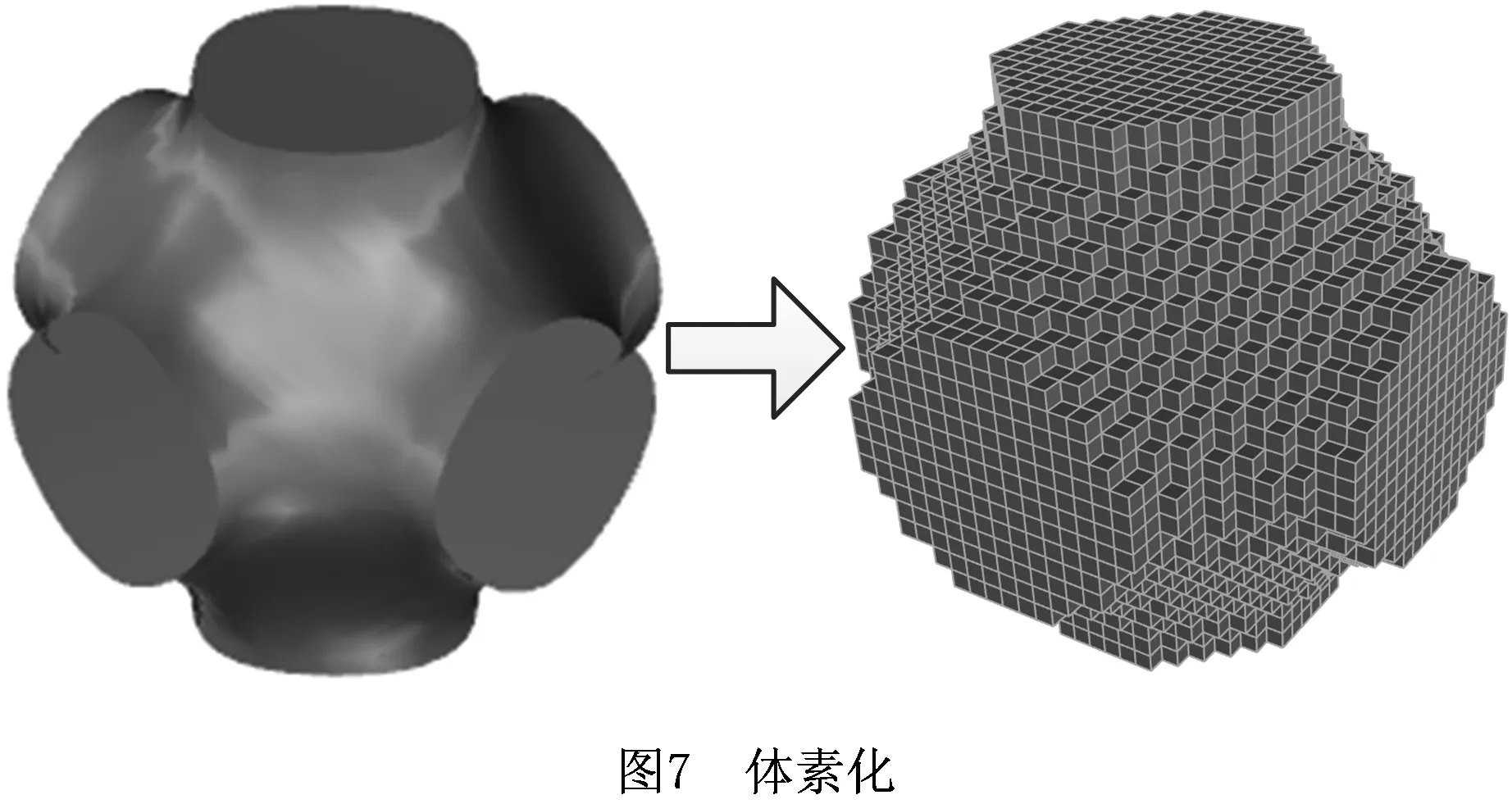
孔隙率
(21)
式中:VP为孔隙体积;VZ为TPMS单元控制六面体体积;m为体素化模型中“1”体素个数,n为体素化模型中所有体素个数,h为体素边长。
(2)孔径
同样采用体素化方法,对TPMS孔隙单元孔径进行计算,通过欧式距离变换,近似求解孔隙单元的最大内接圆直径d。
(22)
式中:r为v层内第i个标记为“1”的体素中心到标记为“0”的体素中心之间的距离,(xvi,yvi,zvi)为第i个被标记为“1”体素中心坐标,(xvj,yvj,yvj)为第j个标记为“0”体素中心坐标。
4 实例设计
为验证设计方法的有效性,本文以局部胫骨三角网格模型为例,从单一孔隙结构设计和梯度孔隙结构设计两方面进行试验,如图8a所示。
4.1 单一孔隙结构设计
(1)不同尺寸体素单元下的多孔结构设计
以P单元作为多孔支架的基本造孔单元,体素单元尺寸h分别设定为5 mm和3 mm,距离函数k值为0,构建的体素化模型如图8b和图8c所示,设计结果如图9所示,多孔结构指标见表1。


(2)不同距离函数k下的多孔结构设计
仍以P单元作为多孔结构支架的基本孔隙单元,体素单元尺寸h设定为3 mm,距离函数k则分别设定为+0.9、+0.7、+0.5、+0.3、+0.1、-0.1、-0.3、-0.5、-0.7、-0.9进行建模,篇幅限制,文中仅给出k=+0.9和k=-0.9下P单元所构建的多孔支架模型,如图10所示,多孔结构指标见表1。

(3)不同TPMS单元下的多孔结构设计
分别以G和F-RD单元作为构建微观孔隙的基本孔隙单元,距离函数k分别设定为:+0.9、0、-0.9,体素单元尺寸仍为3 mm,文中仅给出G单元和F-RD单元k=+0.9下,所构建的多孔支架模型,如图11所示,多孔结构指标见表1。

通过对比实例一的试验结果可以看出,不同体素单元尺寸相同P孔隙单元下所构建的多孔支架,其孔隙结构类似,孔隙率η相同(均为49.37%)。由于孔隙率表征的是孔隙占支架体积的比值,在孔隙单元结构相同的情况下,改变体素单元尺寸对其孔隙率并没有影响,但TPMS孔隙单元尺寸大小受控于体素单元尺寸,实例一中的体素单元尺寸h由5 mm减小到3 mm,孔径由4.28×103μm减小到了2.56×103μm,因此通过改变体素单元尺寸,能够改变孔径大小的尺寸。
通过对比实例二的试验结果可以看出,在相同体素单元尺寸下,虽然均是由P单元构建的多孔支架,但由于距离函数k值的不同,所构造出的多孔结构也不相同。见表1所示,孔径尺寸和孔隙率随着距离函数k值的增大而逐渐增大,且孔隙率变化规律趋向于一条倾斜的直线,采用最小二乘法拟合的一阶直线方程如下:
ηP=28.33×k+50.65。
(23)
式中ηP为孔隙单元P的孔隙率。P单元孔隙率随距离函数k值线性变化的性质,可以方便地实现对多孔结构的控制。当输入自然骨设计所需要的孔隙率时,便可以得到符合要求的孔隙单元。
通过对比实例三的试验结果可以看出,相同体素单元尺寸下,不同类型的TPMS孔隙单元,在不同距离函数k值下,所构建的多孔支架其结构更加多样。综合上述3组实例可以看出,基于TPMS和体素化的多孔骨支架的设计方法,能够实现多孔结构支架设计。

表1 多孔结构指标
4.2 梯度孔隙结构设计
关于梯度结构设计,为方便与单一孔隙结构进行对比,仍以局部胫骨模型为对象进行建模,并在胫骨不同区域实现不同孔隙结构的构建。
(1)不同体素单元尺寸下同类型TPMS孔隙单元不同距离函数k值下的梯度孔隙结构设计
现以P单元作为构建微观孔隙的基本孔隙单元,体素单元尺寸h分别为5 mm和3 mm,在A区域内P单元距离函数k1设定为+0.7,在区域B内P单元距离函数k2设定为0,在区域C内P单元距离函数设定为-0.7,设计结果如图12所示,多孔结构指标见表2。
通过图12b和图12d局部胫骨支架的半剖视图可以看出,所构建的支架内部孔隙结构较为平滑,孔隙结构呈梯度分布。孔隙结构参数如表2所示,过渡区域AB和BC的孔隙率介于其相邻区域之间(区域A、B、C内的孔隙率分别为71.07%,49.37%,31.03%),过渡区域AB:49.37%<55.36%<71.07%,过渡区域BC:31.03%<43.70%<49.37%,且两种体素单元尺寸下,其孔隙率分布没有变化,即对于同一种TPMS单元,在构造梯度孔隙结构时,其局部区域孔隙率主要受控于所装配的孔隙单元的距离函数k值;对于孔径分布,由图12b和图12d,以及表2可以看出,其孔径尺寸自左向右呈逐渐变小趋势,且孔径随体素单元尺寸增大而增大,如在体素单元尺寸3 mm下,过渡区域AB、BC的孔径尺寸分别为2.63×103μm和2.39×103μm,而在5 mm下,孔径尺寸分别为4.36×103μm和4.12×103μm,孔径尺寸增大了近一倍,即通过改变体素单元的尺寸,孔径尺寸大小随之发生变化。因此,对于同类型的TPMS单元,在构造梯度孔隙结构时,可以通过调整局部区域装配的孔隙单元距离函数k值和体素单元尺寸,实现对骨支架孔隙率、孔径大小及其分布的有效控制。

表2 多孔结构指标

实例h/mmη/%d/μm区域A区域AB区域B区域BC区域C区域A区域AB区域B区域BC区域C实例四571.0755.3649.3743.7031.035.024.364.284.123.82371.0755.3649.3743.7031.032.982.632.562.392.21实例五524.1637.2649.3725.4620.591.782.714.282.321.46324.1637.2649.3725.4620.590.611.722.561.380.93
(2)不同体素单元尺寸下不同类型TPMS孔隙单元的梯度孔隙结构设计
以F-RD单元、P单元、G单元为基本孔隙单元,在区域A填充F-RD单元,其距离函数k1为+0.9,在区域B填充P单元,其距离函数k2为0,在区域C填充G单元,距离函数为+0.9,体素单元尺寸h为3 mm。设计结果如图13所示,多孔结构指标如表2所示。
对比图13b和图13d可以看出,不同TPMS单元下构建的孔隙结构变化更为复杂,不同类型TPMS单元间过渡较为平滑,孔隙结构呈梯度分布。与设计实例四相似,过渡区域AB和BC的孔隙率和孔径等结构参数同样介于相邻区域之间,孔隙率(过渡区域AB:24.16%<37.26%<49.37%,过渡区域BC:20.59%<25.46%<49.37%),改变体素单元尺寸大小,对其孔隙率没有影响。对于孔径,由于TPMS单元结构不同,其孔径尺寸自左向右呈现先增大后减小的变化趋势,改变体素单元尺寸,孔径大小随之发生变化。通过上述实验可以看出,通过不同类型的TPMS单元过渡,不但可以丰富支架内部孔隙单元的几何形状,还能够实现对骨支架孔隙率、孔径大小及分布的有效控制。
综合上述试验结果可以看出,本文所提方法能够构建不同孔隙结构排布的模型,实现内部孔隙多样化分布,并能通过控制空间体素单元尺寸、距离函数k、TPMS单元形状等,实现对内部多孔结构的有效控制,这对于克服骨支架建模过程中多孔单元几何形状的限制,制造具有复杂结构组织工程骨支架提供了基础。

5 结束语
本文以TPMS作为基本孔隙单元,采用隐函数表达的TPMS作为构建微观多孔结构的基础孔隙单元,通过定义距离函数及Log-Sigmoid函数,构建了不同结构形式TPMS孔隙单元,克服了骨支架建模过程中孔隙单元几何形状的限制,为制造具有复杂功能梯度多孔骨支架提供了基础。提出了一种逆向几何求交的快速体素化算法,通过网格模型的分层、离散,立方体素填充,实现了对骨支架三角网格模型空间的快速划分,为孔隙单元装配提供了空间区域和位置。多个实例表明,基于三周期极小曲面和体素化的多孔骨支架的设计方法,能够实现多孔结构支架的设计,并能通过对体素单元尺寸、距离函数k、TPMS单元类型等进行控制,构建出不同孔隙结构排布的模型,实现内部孔隙多样化分布,从而为骨支架建模提供了一种新方法。
未来将进一步增加TPMS单元孔隙种类,针对建立孔隙率、生物属性等方面与真实骨结构功能上等价的结构模型进行研究。
