基于高质量过程的指数分布中位数控制图的统计设计
2020-04-08曹程明马义中
曹程明,马义中
(南京理工大学 经济管理学院,江苏 南京 210094)
0 引言
随着现代生产制造技术的不断提高,产品的不合格率或过程缺陷率不断降低,传统p图或c图中的大量打点值为零,造成控制图出现错误警报概率过高、不能提供关于过程状态的有效信息等问题。将不合格品或者过程缺陷的出现定义为事件,监控事件间隔时间(Time Between Events,TBE)能够避免传统控制图在高质量过程监控中的缺陷。Montgomery[1]建议通过TBE监控高质量过程。
假设事件的发生用泊松过程描述,则TBE是一系列独立同分布的指数分布随机变量[2]。针对TBE服从指数分布的过程,Zhang等[3]以r个事件之间的间隔时间服从Gamma分布设计了Gamma控制图(Gamma chart),提高了控制图对过程偏移的探测能力;Yang等[4-5]研究了指数分布控制图(exponential chart)和Gamma控制图,为了应对没有足够样本数据估计参数的情况,提出序贯抽样方案,然而研究没有分析参数估计对其所设计控制图性能的影响。由于参数估计量固有的波动,在同一设计方法下设计出的控制图的性能将出现差异,这种差异被称为使用者与使用者之间的波动(practitioner-to-practitioner variability),该波动令使用者不能确定所设计控制图的错误警报概率,影响了其对控制图的信心。
Jensen等[6]和Psarakis等[7]指出研究参数未知情况下的控制图性能具有重要意义;Saleh等[8]采用运行链长均值ARL的分位数和运行链长均值的标准差SDARL分析了参数未知的指数加权移动平均(Exponentially Weighted Moving Average, EWMA)控制图的性能;Hu等[9]认为ARL和运行链长的标准差SDRL适合用于单个控制图的性能分析,而在参数未知情况下,平均运行链长均值AARL越接近设定值ARL0,说明控制图的性能越接近参数已知的情况,SDARL值越小说明参数估计对控制图性能的影响越小,AARL和SDARL适合分析某一具体设计方法下的控制图的性能。
为了应对实际中样本数据较少的问题,Jones等[10]和Gandy等[11]提出Bootstrap方法,该方法通过调整控制限,使得在一定概率水平下过程受控时控制图的ARL不小于设定值;Zhao等[12]研究了参数未知的c图的性能,并用Bootstrap方法对其控制限进行调整,分析表明Bootstrap方法能够减少参数估计对控制图性能的影响;Hu等[9]研究表明,Bootstrap方法能够使过程受控时控制图的ARL在一定概率水平下不小于设定值,而仅以较小的控制图性能损失为代价。
相比于均值控制图,中位数控制图对样本数据中存在异常值的过程和非正态过程稳健[13]。当总体分布为偏态分布时,中位数能更好地反映样本情况,而且样本中位数易于计算。针对TBE服从指数分布的这一偏态过程,本文提出中位数控制图。首先,给出了参数已知和未知情况下中位数控制图的设计方法;其次,应用条件错误警报概率、AARL和SDARL分析了参数估计对所设计中位数控制图性能的影响;接着,针对小样本问题,采用Bootstrap方法对设计出的控制限进行调整,以减少由参数估计造成的使用者之间的波动问题;最后,用算例说明指数分布中位数控制图在实际中的应用。
1 中位数控制图的设计
1.1 参数已知的情况
假设事件的发生用泊松过程描述,则TBE是独立同分布的指数分布随机变量。用X表示两个连续事件之间的间隔时间,则X的概率密度函数为
(1)
式中λ为事件的发生率。

(2)

(3)

令U和L为控制图的上下控制限,在参数已知的情况下,对于给定的错误警报概率α0,有
(4)
当过程发生偏移时,设偏移量为ρ,λ1=ρλ0。打点值落在控制限之内的概率为
(5)
则控制图的运行链长均值为
(6)
对于双边控制图,如果上下控制限两侧的概率均为α0/2,则ARL在受控状态下(ρ=1)不一定能取得最大值。假设ARL(ρ)对ρ可导,为了使ARL在受控状态下(ρ=1)取得最大值,令
ARL′(1)=0,
(7)
则
(8)
通过式(8)可得
β′(1)=0。
(9)
因此,对于给定的错误警报概率,无偏的中位数控制图的控制限可由下式得到:
(10)
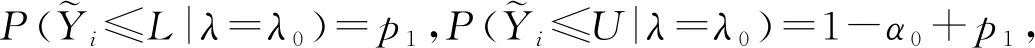
(11)
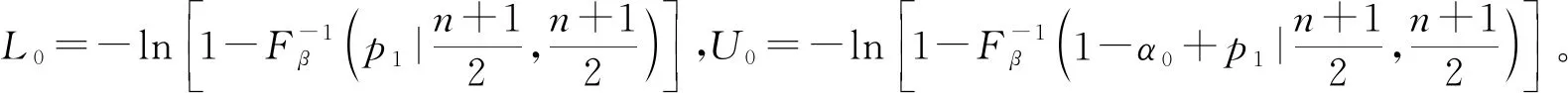
将式(11)代入式(10),通过二分法求解式(10)得到p1。为了便于使用控制图,不同错误警报概率(α0)和不同子组观测值数(n=3,5)的无偏中位数控制图设计参数如表1所示。

表1 控制图的设计参数
1.2 参数未知的情况
在参数未知的情况下,通常通过样本数据估计得到的参数估计值设置控制限参数。假设现有m个服从参数值为λ0的指数分布的观测值样本数据,则λ0的极大似然估计为
(12)
由中位数控制图的无偏设计得参数未知的控制图的控制限为:
2 中位数控制图的性能分析
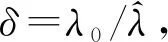
(14)
显然,在参数未知的情况下,样本差异会导致参数估计误差不同,控制图发出信号的概率会随参数估计量的不同而不同。因此控制图发出信号的概率是δ的条件概率,称为条件错误警报概率(CFAR),其揭示了使用者之间的波动。
针对TBE服从指数分布过程的监控问题,Kumar等[14]通过运行链长条件分布研究了参数未知的Tr控制图(Tr-chart),研究结果表明,由于使用者之间的波动,只有当样本数非常大时(大于1 000),参数未知的Tr控制图的性能才能接近参数已知的情况。本章将中位数控制图与Tr控制图的性能进行对比分析。
2.1 中位数控制图的条件错误警报概率
错误警报概率是控制图在过程受控时发出信号的概率,是控制图设计中的一个重要参数。中位数控制图的条件错误警报概率为
(15)
为了便于分析条件错误警报概率,令
(16)
式中Y=2(m-1)×δ服从自由度为2m的χ2分布[14]。为了分析样本数m和子组大小n对α(Y)值的影响,计算n=3,5,m=30,50,200,1 000时的α(Y)值,如图1所示(α0=0.002 7)。为了便于比较中位数控制图和Tr控制图,计算r=3,5,m=30,50,200,1 000时Tr控制图的α(Y)值,如图1所示(α0=0.002 7)。图1每个子图中竖向分隔线将图形分为两部分,在分隔线处α(Y)=α0(Y=2(N-1)),在分隔线的左边δ=Y/2(N-1)<1,表示参数被高估,反之参数被低估。
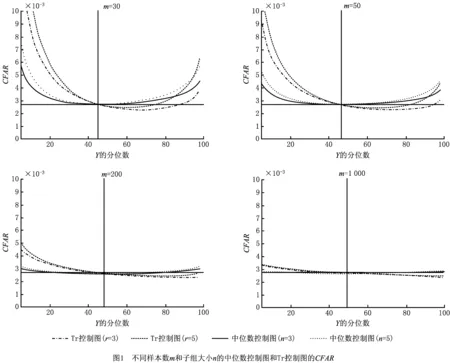
从图1可见,对于所有n和r的取值,在Y的分布的尾部,α(Y)的值均偏离设定值α0,随着样本数的增加,偏离量越来越小,说明参数估计会使控制图的性能产生较大波动,而且随着样本数的增加,其影响越来越小;当样本数相同时,中位数控制图α(Y)的值均比Tr控制图更接近设定值α0,说明参数估计对中位数控制图性能的影响更小;对于中位数控制图,分隔线两侧的α(Y)值均大于α0,说明无论参数被高估还是低估,控制图的CFAR都会变大,相应的ARL变短。
2.2 过程受控时中位数控制图的AARL和SDARL
过程受控时控制图的的条件平均运行链长(ICARL)是CFAR的倒数,因此也看做Y的函数,即
(17)
则
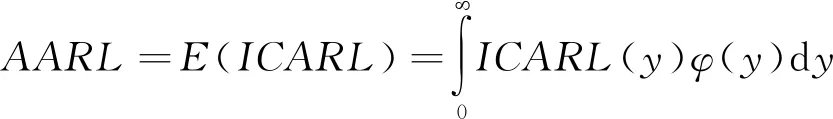
(18)
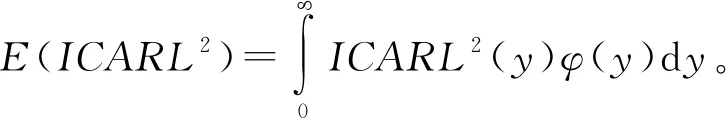

表2 过程受控时中位数控制图和Tr控制图的AARL和SDARL
由表2可见,随着样本数m的增加,中位数控制图和Tr控制图的AARL值越接近设定值ARL0,SDARL值越小,说明随着样本数m的增加,参数未知的控制图的性能越接近参数已知的情况。当子组大小相同时(n=3,r=3或n=5,r=5),相比于Tr控制图,中位数控制图的AARL值更接近设定值ARL0,SDARL值更小。Zhang等[15]建议SDARL值应小于设定值ARL0的10%,对于Tr控制图,当r=3,5时,需要1 000个样本数据才可以使SDARL值小于设定值ARL0的10%,而对于中位数控制图,当n=3时需要100个样本数据,当n=5时需要200个样本数据。
综上所述,相比于Tr控制图,参数估计量的波动对中位数控制图性能的影响更小,使用者用估计参数设计出的控制图的条件错误警报概率值更接近设定值α0,即参数估计量的波动对中位数控制图性能的影响更小。
3 调整控制图的控制限
3.1 控制限调整步骤

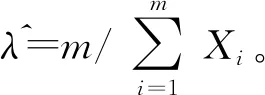
(2)从第一阶段样本数据得到j=1,…,B个Bootstrap样本X1,j,X2,j,…,Xm,j。

(4)由式(19)计算得到kj(j=1,…,B):
(19)
(5)取kj的d%的分位数,即为调整系数k。
d%为调整目标,调整后的控制图的CFAR有d%的可能性不大于设定值α0。B一般取1 000。
3.2 控制限调整前后控制图的性能对比

表3 控制限调整前后过程受控时的ARL小于设定值的百分比 %
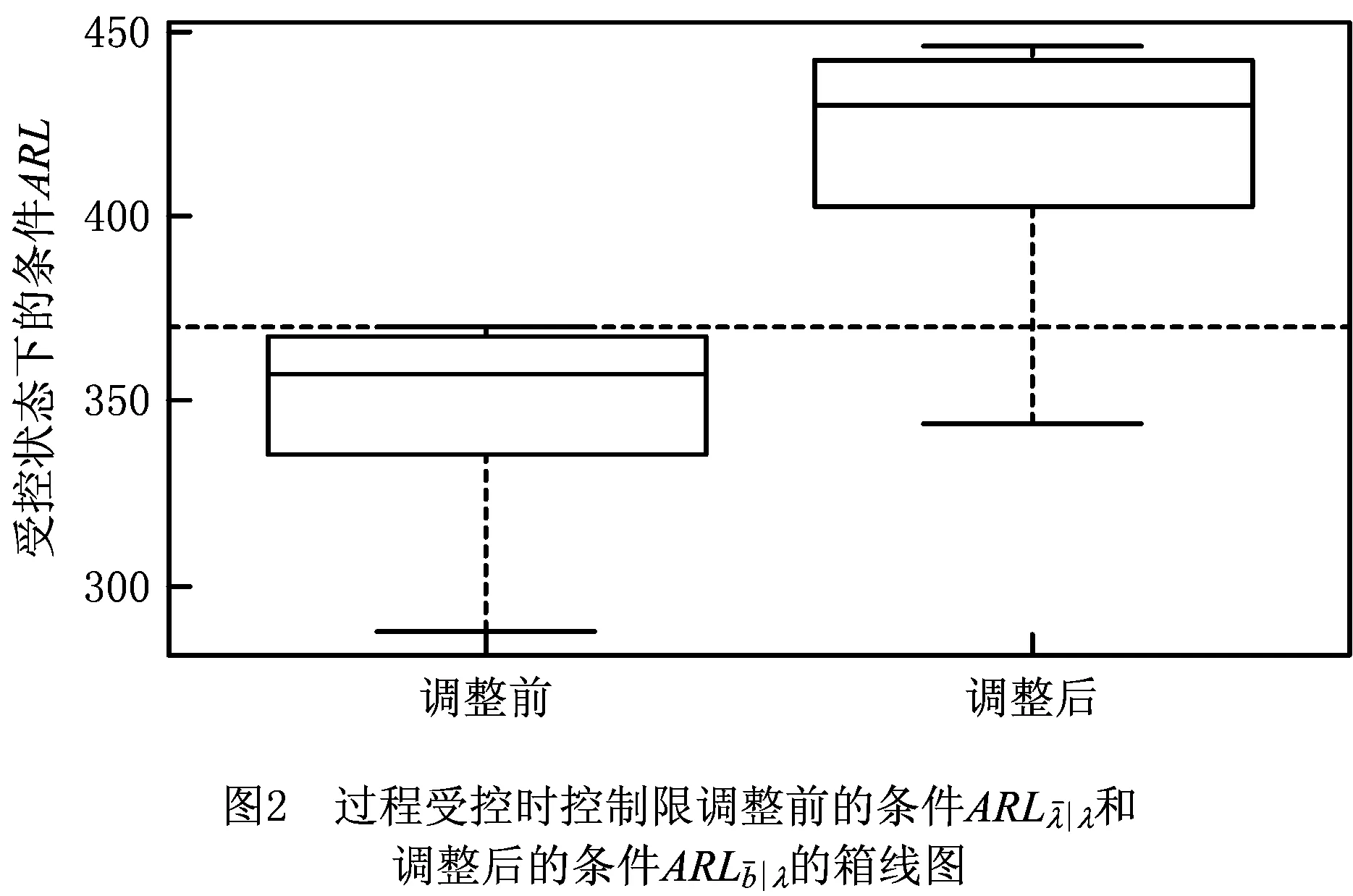
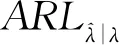

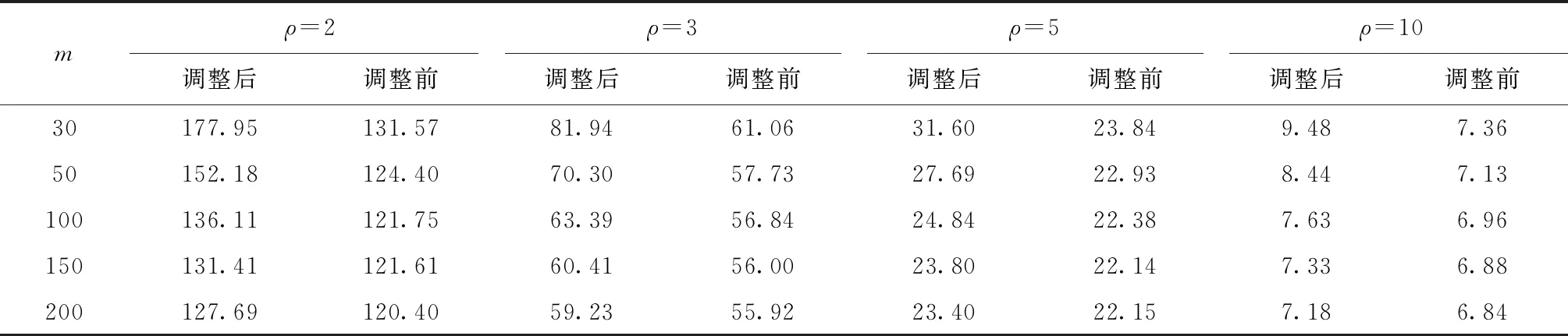
表4 控制限调整前后控制图在过程失控时的AARL

通过对比分析控制限调整前后控制图性能可以看出,控制限调整后的控制图能够使过程受控时的ARL在设定概率水平下不小于设定值ARL0,即调整控制限对控制图探测过程偏移能力的影响小。另外,在仿真过程中注意到,每一次使用Bootstrap方法调整的系数k都不同,但是差别很小。表5和表6所示为m=30,50,100,150,200,α0=0.002,0.002 7,0.005,0.01,n=3,5,d%=0.9时的调整系数k,表中k值为1 000次仿真结果的平均值。在实际使用中,使用者可以直接用表5和表6中的k值,也可以自行计算k。
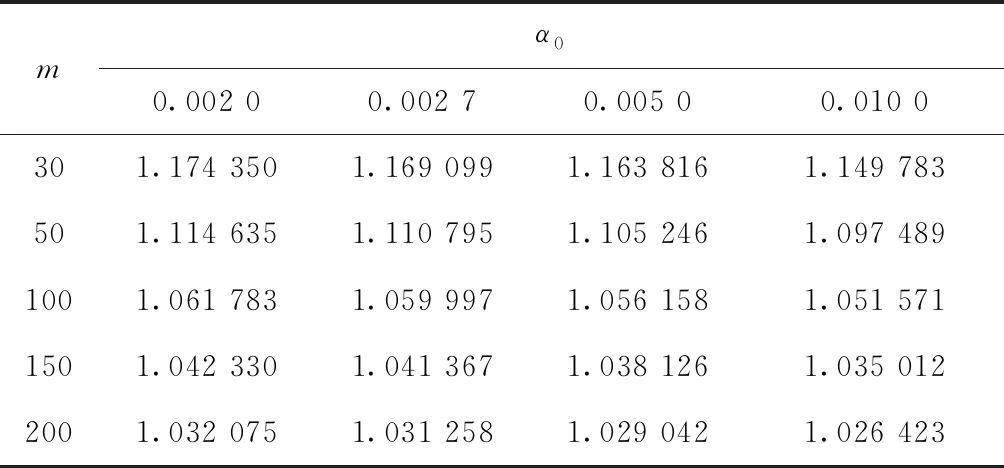
表5 基于Bootstrap方法的调整系数k(n=3)
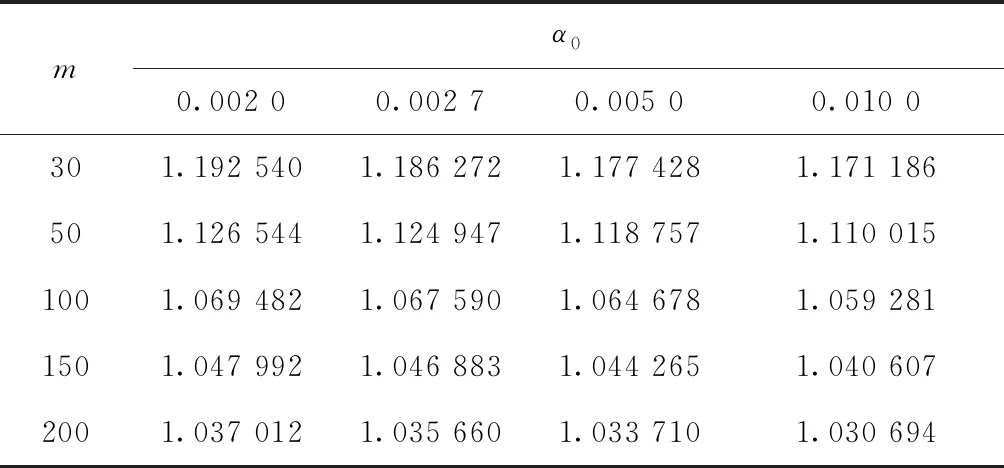
表6 基于Bootstrap方法的调整系数k(n=5)
4 实例分析
5 结束语
本文提出用中位数控制图监控TBE服从指数分布的过程,给出了参数已知和未知情况下中位数控制图的设计方法及控制图设计参数。相比于Tr控制图,本文所设计的中位数控制图在过程受控时,其AARL更接近设定值ARL0,SDARL更小,即参数估计量的波动对中位数控制图性能的影响更小。
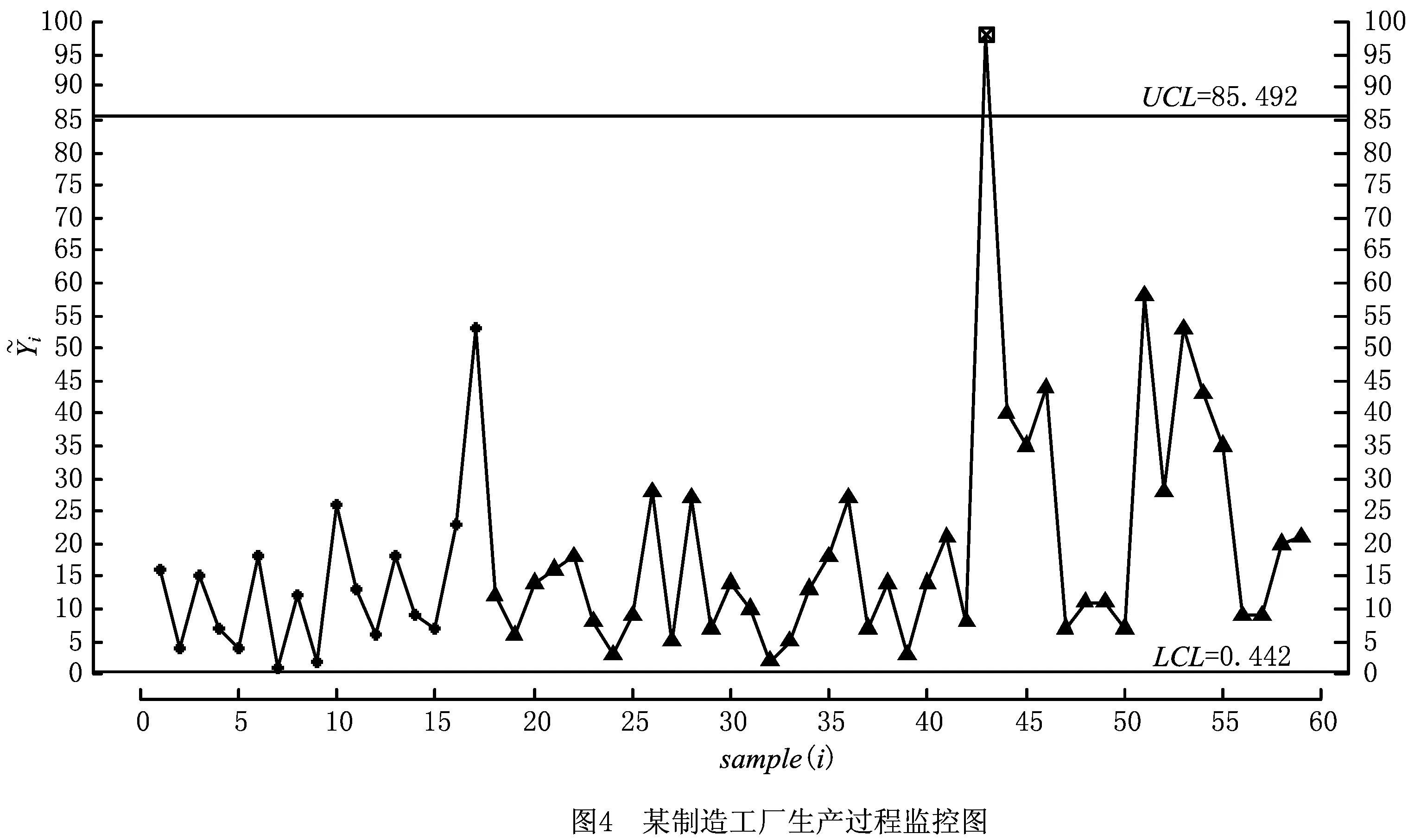
针对小样本问题(m<200时),用Bootstrap方法调整所设计控制图的控制限,调整后的控制限能够有效减少参数估计量波动对控制图性能的影响。实例分析表明,指数分布中位数控制图对过程偏移具有较好的检出能力。当参数未知时,本文使用极大似然估计方法估计过程参数,并未考虑到过程的先验信息,后续研究可以结合贝叶斯估计方法设计指数分布的中位数控制图。
