浅埋软弱围岩隧道超前管幕施工力学行为分析
2020-04-08戴光耀1孙宁新龙1曹豪荣张运良
戴光耀1, 孙宁新, 彭 龙1, 曹豪荣, 张运良
(1. 中交第三航务工程局有限公司, 上海 200032; 2.中南大学 土木工程学院, 湖南 长沙 410075)
隧道修建过程中,时常会穿越一些特殊地质地段,如软弱围岩、膨胀土、流沙、松散地层等,特别是当隧道埋深较浅时,施工过程中极易产生大变形和洞室失稳现象。因对浅埋软弱围岩隧道支护体系的力学机理认识不清而采取不当的施工控制措施,从而引发安全事故的工程案例屡见不鲜。鉴于此,国内外学者对浅埋软弱围岩隧道支护结构的力学机理进行了深入研究,研究成果众多[1-4]。但缺乏统一认识,且主要针对单一构件的作用机理进行研究,缺乏对各构件协同作用的研究,使结果偏于保守。
本文依托京沈高铁高丽营隧道工程,分别采用荷载结构法和地层结构法进行数值模拟,综合考虑围岩自承作用和支护体系的协同作用,对荷载作用下超前管幕的力学行为进行分析。同时,通过开展理论计算,对比了2种数值模拟方法与理论计算的差异,对类似隧道工程的设计、施工具有指导意义。
1 工程背景
京沈高铁高丽营隧道地处北京顺义、昌平郊区,隧道全长1 200 m,其中DK33+730~DK34+160段为暗挖隧道工程。该段隧道覆土厚度仅5.0~7.2 m,穿越地层以黏土为主,属Ⅵ级围岩,为典型的浅埋软弱围岩隧道。隧道暗挖段纵断面如图1所示。
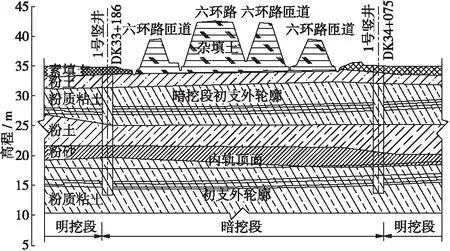
图1 隧道暗挖段纵断面图
由于隧道埋深浅,围岩等级低,下穿结构物多,隧道暗挖段全断面采用双侧壁导坑法与管幕相结合的施工方法。基于新奥法原理对暗挖段隧道支护体系进行设计,采用复合式衬砌结构:以锚管、钢筋网、喷射混凝土作为初期支护,模筑钢筋混凝土作为二次衬砌。初期支护和二次衬砌之间设置防水层。下穿暗挖段采用双层衬砌,二衬和三衬之间设置防水层。
隧道穿越黏土层,按双侧壁导坑七台阶开挖,开挖步长0.5 m。超前管幕沿隧道外轮廓线均匀布置,长30 m,共设55根。水平方向直线打设,纵向按线路纵坡坡度设置10°倾角。图2为隧道暗挖段管幕布置示意图。

图2 隧道暗挖段管幕布置示意图
2 荷载结构法数值模拟
2.1 模型信息
隧道支护体系由超前Φ299管幕、锁脚锚管及钢拱架组成,采用三结点空间线性梁单元进行模拟,可以在保证精度的同时,优化各支护结构之间的接触关系[5]。根据工程实况,利用ABAQUS有限元软件,采用荷载结构法建立隧道支护体系的三维数值计算模型,见图3。构件的材料参数如表1所示。

图3 隧道支护体系计算模型
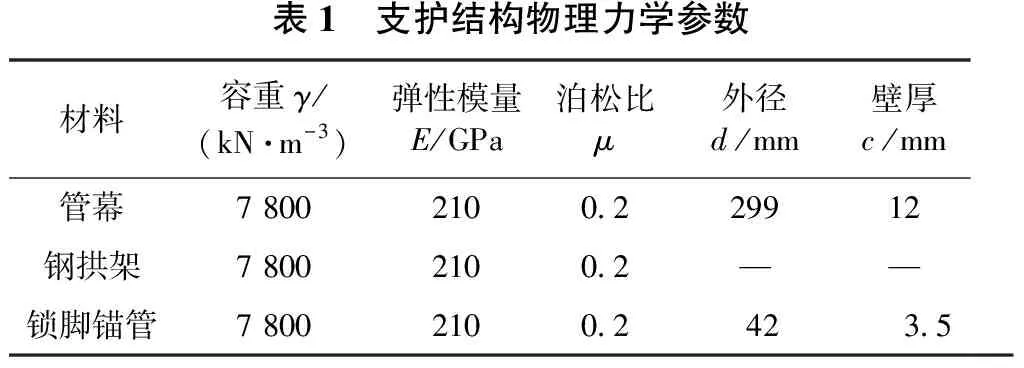
表1 支护结构物理力学参数材料容重γ/(kN·m-3)弹性模量E/GPa泊松比μ外径d/mm壁厚c/mm管幕7 8002100.229912钢拱架7 8002100.2——锁脚锚管7 8002100.2423.5
2.2 围岩荷载
根据勘查设计资料,隧道暗挖段开挖宽度15.2 m,开挖高度13.18 m,覆土厚度7.2 m。土层分为2层,即粉土层(0~5 m)和黏土层(6~20 m)。围岩物理力学参数见表2。
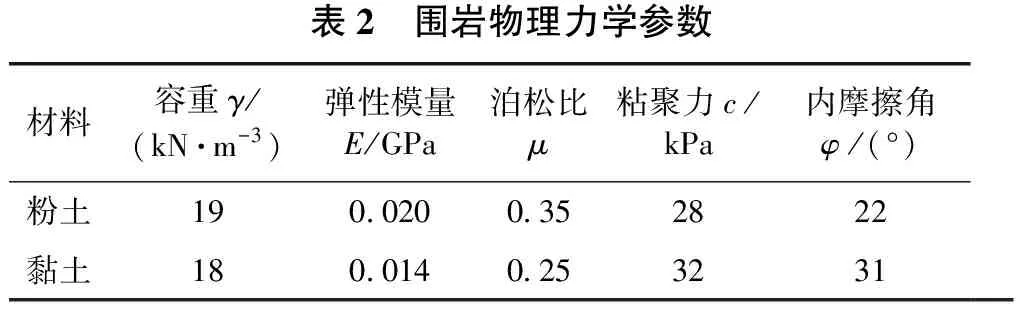
表2 围岩物理力学参数材料容重γ/(kN·m-3)弹性模量E/GPa泊松比μ粘聚力c/kPa内摩擦角φ/(°)粉土190.0200.352822黏土180.0140.253231
李玉峰等[6]基于太沙基破坏模式,构建了线性与非线性破坏准则下,浅埋复合地层隧道围岩压力的计算方法。表3给出了基于该方法求得的拱顶及左侧共28根管幕支护范围内的径向均布荷载(左右对称位置的超前管幕所受均布荷载值相同)。

表3 管幕径向均布荷载管幕位置荷载大小/ Pa管幕位置荷载大小/Pa拱顶1#104 995左侧15#107 930左侧2#105 010左侧16#108 560左侧3#105 040左侧17#109 310左侧4#105 090左侧18#110 220左侧5#105 170左侧19#111 310左侧6#105 270左侧20#112 660左侧7#105 400左侧21#114 320左侧8#105 560左侧22#116 420左侧9#105 760左侧23#119 110左侧10#105 990左侧24#122 610左侧11#106 260左侧25#127 280左侧12#106 580左侧26#133 710左侧13#106 960左侧27#142 840左侧14#107 410左侧28#156 400
2.3 超前管幕力学行为分析
将2.2节所求得的围岩荷载施加到支护体系的有限元模型上,计算得到各支护结构的力学响应。
2.3.1内力分析
图4为采用荷载结构法模拟得到的隧道暗挖段超前管幕的内力云图。分析可知:
1)轴力关于隧道轴线呈正对称分布;同一断面,轴力由中间管幕向两侧递减。轴力(拉力)的最大值为63.78 kN,位于围岩松弛段的中间管幕处;轴力(压力)最小值为-125.2 kN,主要分布在洞口处和已开挖未支护段。


a)轴力b)剪力

c) 弯矩
2) 剪力关于隧道轴线呈反对称分布,同一断面,外侧管幕的剪力值大于中间管幕的剪力值,剪力最大值为676.3 kN。
3)弯矩分布规律与剪力分布规律相似,弯矩最大值为53.05 kN·m,分布在围岩松弛段。
2.3.2变形分析
图5a是超前管幕在荷载作用下的竖向位移云图;图5b是1#管幕的竖向位移曲线。
由图可知:

a) 管幕竖向位移云图
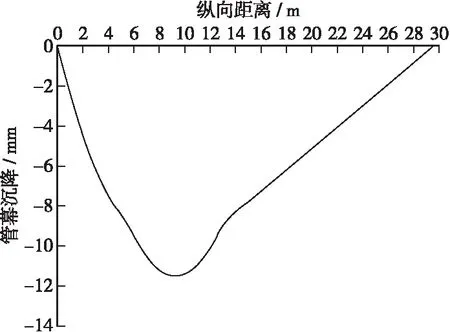
b)1#管幕竖向位移图
1) 同一隧道断面,由于外侧管幕埋深较中间管幕大,所承受的围岩荷载也更大,故其竖向位移值大于中间管幕的竖向位移值。
2) 1#管幕挠度的最大值为11.17 mm,位于掌子面前方围岩松弛段,挠度曲线整体上呈“凹型”,近似于Peck沉降曲线。
3 地层结构法数值模拟
3.1 模型信息
确定隧道埋深为7.2 m,围岩(隧道居中)横向取160 m,竖向取80 m,纵向取30 m。喷射混凝土、临时支撑采用四结点曲面薄壳单元进行模拟;超前管幕、锁脚锚管及钢拱架采用三结点空间线性梁单元进行模拟。隧道支护体系空间位置如图6所示。
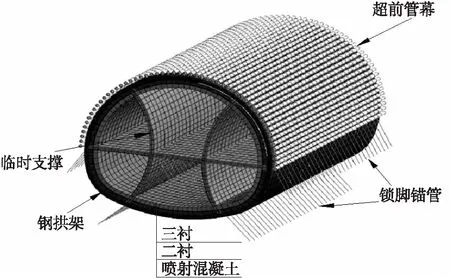
图6 隧道支护体系空间位置示意图
土体分为3层,即粉土(0~5 m)、黏土(6~20 m)和砂土(21~80 m),采用地层结构法模拟双侧壁导坑法施工。
3.2 超前管幕力学行为分析
3.2.1内力分析
超前管幕以水平方式打入掌子面前方土体,管幕端部与钢拱架牢固焊接,与围岩共同变形,其沉降与其所处位置处土体趋于一致。图7为各施工工序对应的超前管幕弯矩云图,分析可知:
1)沿隧道掘进方向,越靠近掌子面的管幕弯矩越大,远离掌子面的管幕弯矩较小。
2)弯矩分布由掌子面后方管幕下部受拉过渡到掌子面前方管幕下部受拉,最后在掌子面上方,弯矩达到最大值。
3)随着施工工序的不断推进,同一隧道断面,管幕弯矩的最大值逐步增大,并从左导坑附近逐步移动到拱顶正上方,由此可见,超前管幕是较为有效的承载构件。

a) 开挖左上导坑

b) 开挖左下导坑

c) 开挖右上导坑d)

d) 开挖右下导坑

e) 开挖上台阶

g) 开挖下台阶
4)从施工工序分析,开挖右上导坑对超前管幕弯矩最大值影响最大,增长率达到了36.2%;其次为开挖右下导坑,相比之下,开挖下台阶对管幕弯矩最大值影响最小。
3.2.2变形分析
图8为1#管幕在不同工序下的竖向位移曲线。表4为不同施工工序下1#管幕竖向位移最大值变化表。分析可知:
1) 不同施工步下,1#管幕竖向沉降曲线均为“凹型”,类似于Peck沉降曲线;各施工步均在掌子面附近达到竖向位移的最大值。
2) 沿隧道掘进方向,距离掌子面越近的管幕竖向沉降越大,而远离掌子面的管幕沉降值减小,并不断趋于0。
3) 不同施工工序对1#管幕竖向沉降的影响不同,开挖右下导坑影响最大,该施工步1#管幕竖向沉降增长率达到了98.29%;其次为开挖上台阶,相较而言,开挖下台阶对1#管幕竖向沉降的影响最小。

图8 1#管幕竖向位移曲线
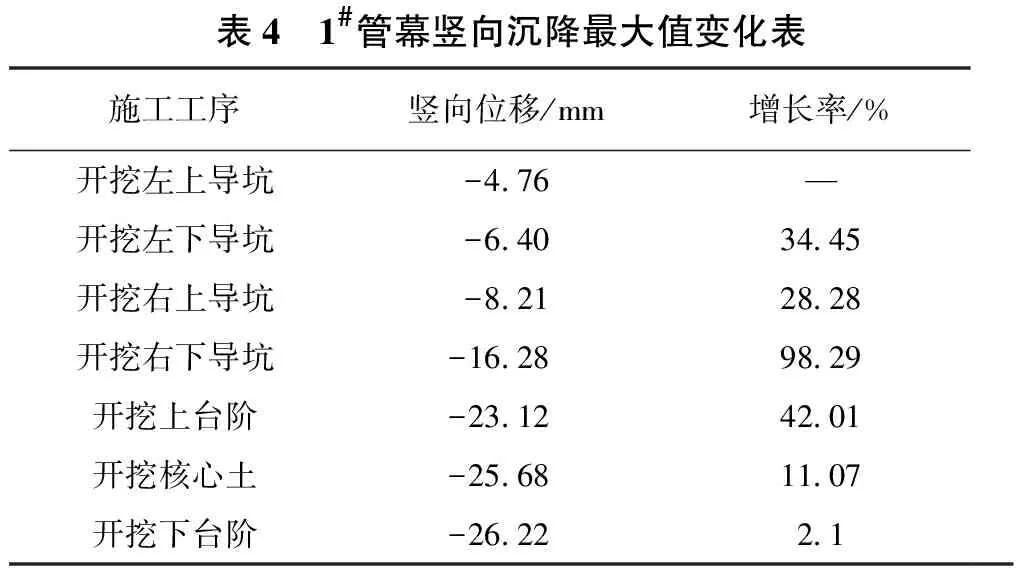
表4 1#管幕竖向沉降最大值变化表施工工序竖向位移/mm增长率/%开挖左上导坑-4.76—开挖左下导坑-6.4034.45开挖右上导坑-8.2128.28开挖右下导坑-16.2898.29开挖上台阶-23.1242.01开挖核心土-25.6811.07开挖下台阶-26.222.1
4 结果分析
4.1 理论计算
取隧道暗挖段1#管幕为分析对象,进行理论计算。按李玉峰等[6]提出的浅埋复合地层隧道围岩压力计算方法,可得基于管幕半无限长弹性地基梁的1#管幕已开挖支护段挠度曲线表达式为:
由上式计算可得1#管幕不同位置的挠度值,如表5所示,1#管幕的理论挠度曲线如图9所示。
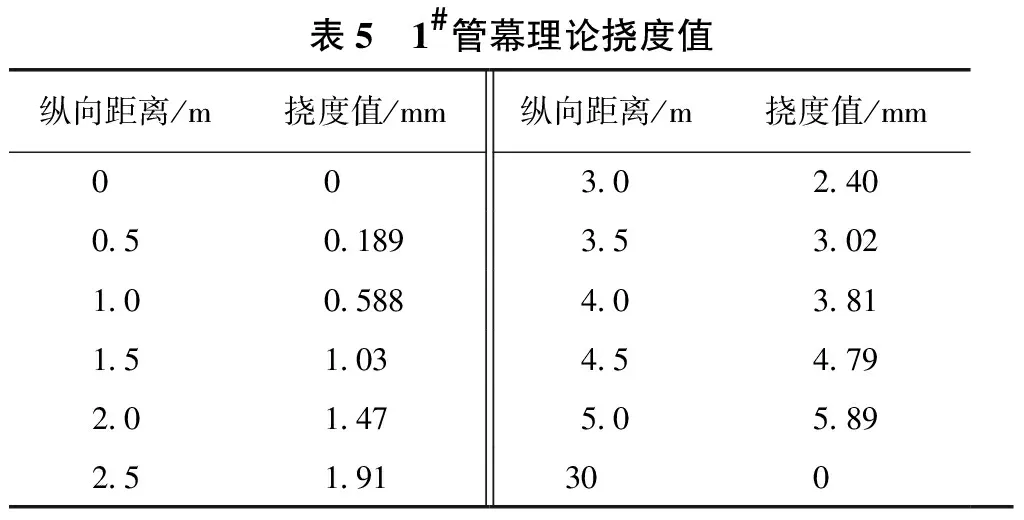
表5 1#管幕理论挠度值纵向距离/m挠度值/mm纵向距离/m挠度值/mm003.02.400.50.1893.53.021.00.5884.03.811.51.034.54.792.01.475.05.892.51.91300
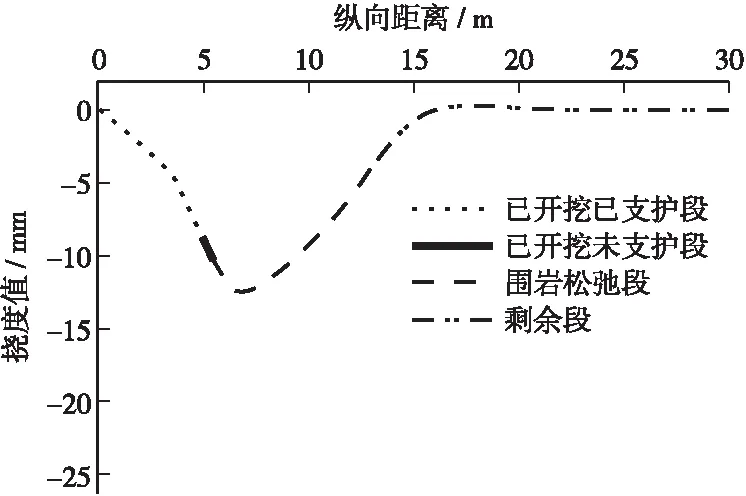
图9 1#管幕理论挠度曲线
4.2 对比分析
将2.3节和3.2节中通过荷载结构法和地层结构法分别得到的隧道暗挖段1#管幕挠度曲线与理论分析求得挠度曲线进行对比分析,见图10。分析可知:
1) 1#管幕的理论挠度曲线与荷载结构法数值模拟得到的挠度曲线形状相似,而与地层结构法得到的曲线相差较大。
2) 理论挠度曲线与荷载结构法数值模拟曲线的峰值比较接近,且均是在掌子面前方围岩松弛段达到挠度最大值,而地层结构法的峰值出现在掌子面处。
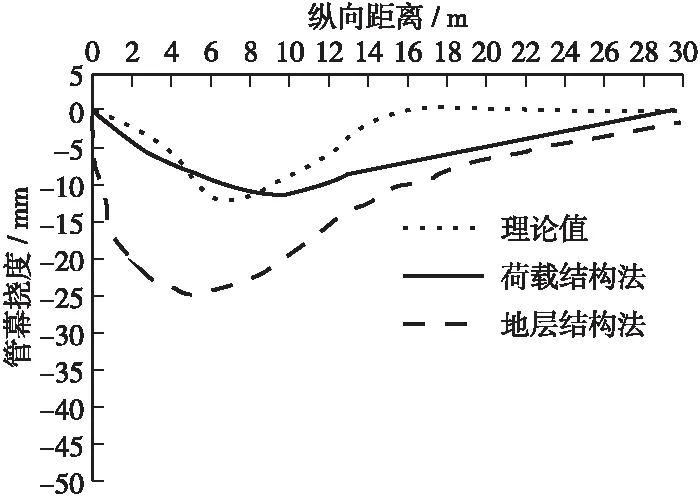
图10 1#管幕挠度曲线对比图
3) 理论曲线由于边界条件和初始参数的设置,在距掌子面5 m范围内挠度值已趋于0,而荷载结构法数值模拟解却有一个渐变的过程。
4) 3条曲线共同点是在管幕初始锚固端竖向沉降值为0,管幕无限远处竖向沉降值也为0。
5 结论
1) 荷载结构法数值模拟中,管幕轴力关于隧道轴线呈正对称分布,剪力和弯矩关于隧道轴线呈反对称分布。
2) 在地层结构法数值模拟中,沿隧道掘进方向越靠近掌子面的管幕弯矩越大;不同施工工序对管幕弯矩变化的影响程度不同,开挖右上导坑影响最大。
3) 将高丽营隧道1#管幕理论挠度曲线与2种数值模拟求得的挠度曲线进行对比分析,结果表明: ① 3条曲线的分布规律各有差异,但理论挠度曲线与荷载结构法数值模拟得到的挠度曲线,形状相似,而与地层结构法得到的曲线与前两者相差较大。② 3条曲线共同点是在管幕初始锚固端竖向沉降值为0,管幕无限远处竖向沉降值也为0。③ 通过分析可认为,采用荷载结构法对浅埋软弱围岩隧道支护体系进行模拟分析时,计算结果更接近工程实际。
