墩高差对大跨连续刚构桥地震响应的影响分析
2020-04-08
(湖南省交通科学研究院有限公司 交通建设工程湖南省重点实验室, 湖南 长沙 410015)
0 引言
我国近年来修建了不少的大跨径连续刚构桥,但大部分都没有经历强烈地震的考验,因此这类桥型非常缺少地震破坏的有关资料,并且十分缺乏较成熟的抗震设计经验[1-4]。研究此类桥型结构参数对地震响应特性的影响,对其抗震设计有相当重要的作用。本文通过工程实例建立了3种不同墩高差的模型,从结构位移和内力两方面来探讨墩高差对大跨连续刚构桥的地震响应影响规律。
1 工程概况
本文研究对象为张花高速花垣至里耶连接线的里耶特大桥,该桥位于连接线K40+497~K40+859处,地处湖南省龙山县里耶镇。桥梁全长350 m,是桥跨布置为(91+168+91)m的连续刚构桥。桥面全宽12.5 m,桥面布置:0.25 m(人行道护栏)+1 m(人行道)+0.5 m(防撞护栏)+9 m(行车道)+0.5 m(防撞护栏)+1 m(人行道)+0.25 m(人行道护栏)。桥梁总体布置图如图1所示。

图1 里耶特大桥桥型布置图(单位: m)
2 有限元模型建立
进行地震响应分析时,考虑桩-土相互作用,全桥采用空间梁单元来模拟,共有243个节点和228个单元;墩顶与主梁采用弹性连接中的刚性连接,桩周采用节点弹性支承模拟土体与桩基的相互作用;承台与桩基之间采用刚性连接,本桥桩基础底部为嵌岩桩,因此桩基底部边界条件采用墩底固结。有限元模型建立如图2所示。节点弹性支承的刚度涉及到等代土弹簧[5]的计算,等代土弹簧采用《公路桥涵地基与基础设计规范》(JTG D63—2007)中的“m法”进行计算[6],具体计算结果见表1。

图2 考虑桩-土相互作用的里耶特大桥有限元模型图

表1 里耶特大桥桩周等代土弹簧刚度土层1#墩2#墩土层厚度/mKx/103 kN·m-1()Ky /103 kN·m-1()土层厚度/mKx/103 kN·m-1()Ky /103 kN·m-1()土层1102 5202 52092 041.22 041.2土层2107 5607 56096 123.66 123.6土层31012 60012 600910 206.010 206.0土层41017 64017 640914 288.414 288.4 注: Kx表示桩基等代土弹簧顺桥向刚度;Ky表示桩基等代土弹簧横桥向刚度。
2.1 参数拟定
里耶特大桥1#墩墩高为40.43 m,2#墩墩高为36.77 m,为了比较不同的墩高差对结构地震响应的影响,以模型B为基础,保持1#墩墩高为40 m不变,从50 m开始,以10 m为一级逐级增高2#墩墩高,为了得出较为直观的结论,建立了3种不同的墩高差模型,具体墩高及墩高差参数见表2。

表2 3种模型墩高及墩高差m模型1#墩墩高2#墩墩高墩高差模型1405010模型2406020模型34070 30
2.2 结构动力特性计算
通过计算结构的自振频率与各向基频的大小,能够得出结构的整体刚度分布情况[7]。本条采用多重Ritz向量法求取各模型的前10阶自振频率及振型[8],计算结果见表3及图3。
根据表3及图3可知,结构墩高差的变化对结构振型特点无影响,但造成了其各向自振频率的改变。随着结构墩高差的增大,结构在纵向、横向以及竖向的基频均有所降低。对比模型1与模型2,纵向基频降低了8.27%,横向基频降低了10.93%,竖向基频降低了0.21%。对比模型2与模型3,纵向基频降低了6.43%,横向基频降低了8.88%,竖向基频降低了0.18%。由此可知,桥墩高差的变化对结构的纵、横向基频影响较大,对竖向基频影响较小,且墩高差越大,各向基频越小;对于结构的低阶振型影响明显,对高阶振型影响较小[9]。

表3 3种模型自振频率与振型对比振型阶次模型1模型2模型3频率/Hz振型特点频率/Hz振型特点频率/Hz振型特点10.447 318对称横弯0.398 417对称横弯0.363 021对称横弯20.674 956反对称竖弯0.619 157反对称竖弯0.579 331反对称竖弯30.766 502反对称横弯0.740 849反对称横弯0.726 620反对称横弯40.982 047反对称横弯0.963 787反对称横弯0.950 437反对称横弯51.238 258对称横弯1.228 064对称横弯1.221 439对称横弯61.736 352反对称竖弯1.687 547反对称竖弯1.652 205反对称竖弯71.939 146对称竖弯1.935 062对称竖弯1.931 565对称竖弯82.069 833反对称横弯2.064 909反对称横弯2.061 366反对称横弯92.534 950反对称竖弯2.524 497反对称竖弯2.513 969反对称竖弯103.093 849对称横弯3.074 406对称横弯3.048 644对称横弯

图3 墩高差与基频的变化关系
3 位移分析
忽略竖向位移响应,各关键截面顺桥向与横桥向位移响应见表4及图4、图5。
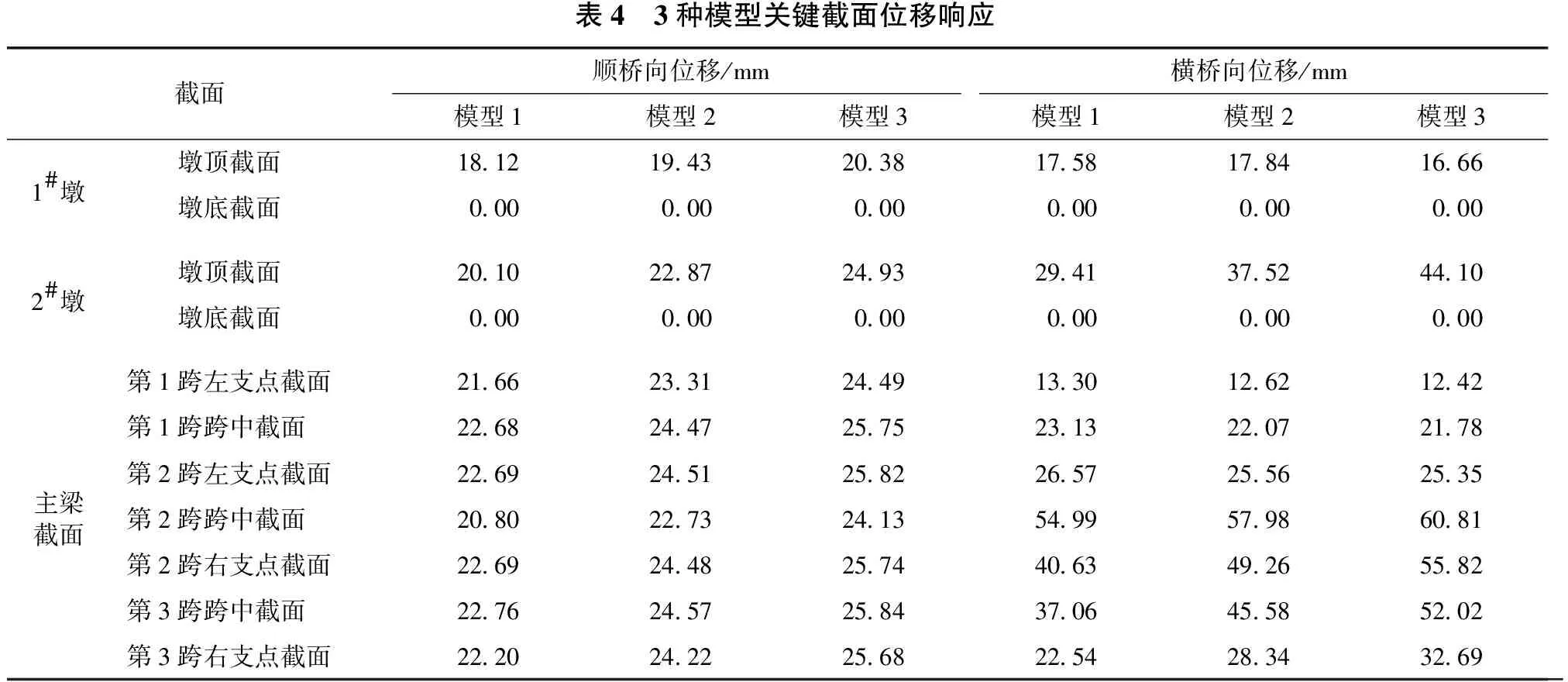
表4 3种模型关键截面位移响应截面顺桥向位移/mm横桥向位移/mm模型1模型2模型3模型1模型2模型31#墩 墩顶截面18.12 19.43 20.38 17.58 17.84 16.66 墩底截面0.00 0.00 0.00 0.00 0.00 0.00 2#墩 墩顶截面20.10 22.87 24.93 29.41 37.52 44.10 墩底截面0.00 0.00 0.00 0.00 0.00 0.00 第1跨左支点截面21.66 23.31 24.49 13.30 12.62 12.42 第1跨跨中截面22.68 24.47 25.75 23.13 22.07 21.78 第2跨左支点截面22.69 24.51 25.82 26.57 25.56 25.35 主梁截面第2跨跨中截面20.80 22.73 24.13 54.99 57.98 60.81 第2跨右支点截面22.69 24.48 25.74 40.63 49.26 55.82 第3跨跨中截面22.76 24.57 25.84 37.06 45.58 52.02 第3跨右支点截面22.20 24.22 25.68 22.54 28.34 32.69

图4 纵向位移对比图

图5 横向位移对比图
由表4、图4、图5可知:
随着墩高差的增加,主梁与主墩的顺桥向位移均逐渐增大,且高墩增幅明显大于矮墩。墩高差由10 m变到20 m,主墩顺桥向位移最大增幅达13.78%,主梁中跨跨中截面增幅最大,达到了9.28%。墩高差由20 m变到30 m,主墩顺桥向位移最大增幅达9.01%,主梁中跨跨中截面增幅最大,达到了6.16%。随着墩高差的增加,主墩与主梁横桥向位移均有增有减,由于矮墩保持40 m高度不变,高墩高度增加时,导致矮墩墩顶及附近3个主梁截面横桥向位移均有所下降;高墩墩顶与附近主梁截面则有明显的增幅。
4 内力分析
忽略竖向内力响应,各关键截面顺桥向内力响应见表5及图6、图7,横桥向内力计算结果见表6及图8、图9。

表5 3种模型关键截面顺桥向内力响应截面顺桥向剪力/kN顺桥向弯矩/(kN·m)模型1模型2模型3模型1模型2模型31#墩 墩顶截面4 691.31 4 906.96 5 088.07 70 251.4470 765.0671 848.89 墩底截面5 133.005 300.65 5 450.10 133 080.80140 067.64145 547.262#墩 墩顶截面3 320.49 2 422.33 1 723.94 77 013.5975 759.5071 040.06 墩底截面3 971.81 3 248.41 2 879.46 110 300.6596 126.7484 477.03第1跨左支点截面722.84 765.67 809.89 37 261.5340 263.1242 352.37第1跨跨中截面1 352.82 1 248.40 1 212.12 50 164.5656 207.2061 197.56第2跨左支点截面981.40 1 074.72 1 152.65 41 470.3440 954.7342 199.25主梁截面第2跨跨中截面1 072.15 985.96 920.07 5 982.009 425.5511 647.19第2跨右支点截面1 126.72 1 258.23 1 322.55 61 682.8667 164.9769 074.86第3跨跨中截面1 308.54 1 205.88 1 155.56 35 556.2928 293.8923 797.49第3跨右支点截面513.94 414.46 359.96 24 596.6719 149.7916 492.10

图6 顺桥向剪力对比图

图7 顺桥向弯矩对比图
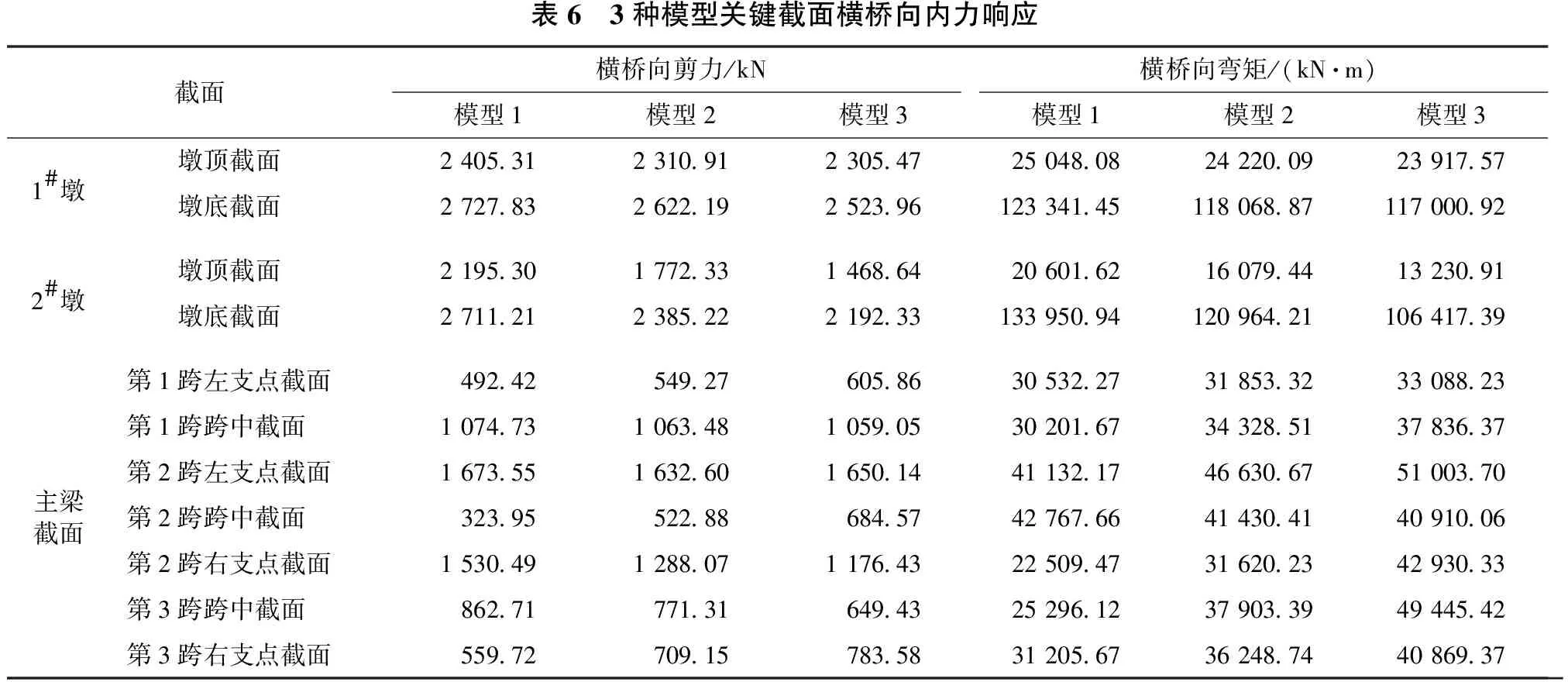
表6 3种模型关键截面横桥向内力响应截面横桥向剪力/kN横桥向弯矩/(kN·m)模型1模型2模型3模型1模型2模型31#墩 墩顶截面2 405.31 2 310.91 2 305.47 25 048.0824 220.0923 917.57 墩底截面2 727.83 2 622.19 2 523.96 123 341.45118 068.87117 000.922#墩 墩顶截面2 195.30 1 772.33 1 468.64 20 601.6216 079.4413 230.91 墩底截面2 711.21 2 385.22 2 192.33 133 950.94120 964.21106 417.39第1跨左支点截面492.42 549.27 605.86 30 532.2731 853.3233 088.23第1跨跨中截面1 074.73 1 063.48 1 059.05 30 201.6734 328.5137 836.37第2跨左支点截面1 673.55 1 632.60 1 650.14 41 132.1746 630.6751 003.70主梁截面第2跨跨中截面323.95 522.88 684.57 42 767.6641 430.4140 910.06第2跨右支点截面1 530.49 1 288.07 1 176.43 22 509.4731 620.2342 930.33第3跨跨中截面862.71 771.31 649.43 25 296.1237 903.3949 445.42第3跨右支点截面559.72 709.15 783.58 31 205.6736 248.7440 869.37

图8 横桥向剪力对比图

图9 横桥向弯矩对比图
由表5、表6及图6~图9可知,随着墩高差的增加,矮墩顺桥向剪力和弯矩均增大,高墩顺桥向剪力和弯矩均减小。当墩高差由10 m增加到30 m时,矮墩墩顶顺桥向剪力增幅达8.46%,弯矩增幅达2.27%。高墩墩顶顺桥向剪力降幅达48.08%,弯矩降幅达7.76%。矮墩墩底顺桥向剪力增幅达6.18%,弯矩增幅达9.37%。高墩墩底顺桥向剪力降幅达27.50%,弯矩降幅达23.41%。主梁各关键截面顺桥向剪力和弯矩随墩高差的增加有增有减。
随着墩高差的增加,主墩横桥向剪力和弯矩均有所减小。当墩高差由10 m增加到30 m时,高墩墩顶横桥向剪力减小了33.10%,弯矩减小35.78%。矮墩墩顶横桥向剪力减小了4.15%,弯矩减小4.51%。高墩墩底横桥向剪力减小了19.14%,弯矩减小20.55%,矮墩墩底横桥向剪力减小了19.14%,弯矩减小20.55%。主梁各关键截面横桥向剪力随墩高差的增加而有增有减,横桥向弯矩除中跨跨中截面有所减小外,其余截面均有不同程度的增幅。
5 结论
本文通过反应谱法进行里耶特大桥地震响应的计算,通过改变里耶特大桥的墩高差,分析了结构的地震响应,得出以下结论:
1) 桥梁墩高差的改变对高墩的横桥向和顺桥向位移影响大于低墩的,当墩高差存在时,高墩水平向位移均会产生较大增幅,且墩高差越大位移增幅越大,应注意地震作用对高墩墩顶的位移影响。
2) 随着墩高差的增大,矮墩截面顺桥向弯矩、剪力均增大,高墩截面顺桥向弯矩、剪力均减小;主梁截面顺桥向弯矩大部分增大;顺桥向剪力有增有减,未表现出明显规律。主梁截面横桥向弯矩大部分增大;横桥向剪力有增有减,未表现出明显规律。因此墩高差越大,对矮墩及主梁内力影响较大,设计时应重点关注。
综上所述,墩高差主要影响的是高墩墩顶位移与矮墩墩底内力,墩高差越大,高墩墩顶位移与矮墩墩底内力越大。因此,对于存在墩高差的桥梁,应着重考虑高墩的抗推刚度与矮墩的截面抗力。
