孔隙度对黏性土渗透系数影响的试验研究

2020-04-08杨忠翰李明宝

科学技术与工程 2020年3期

杨忠翰，李明宝，张旭

(东北林业大学土木工程学院，哈尔滨 150040)

土体的渗透性及渗透系数是岩土工程中十分重要的研究方向，在垃圾填埋场的滤液污染、水利工程的渗漏、地面地基沉降量以及水土压力的计算等实际工程中都起着决定性作用[1-2]。土体作为一种由土颗粒、孔隙水和空气组成的三相松散多孔介质，土颗粒组成土体的骨架，而孔隙水和空气则存在于土体内部土颗粒之间相互连通的孔隙之中。渗流是指土体内部的孔隙水在水头差的作用下流经土颗粒骨架之间相互连通孔隙的现象。而渗透性是指土体允许水或其他流体流经其内部的性能[2]。土体的渗透性研究对于建筑工程选址、基坑工程的防水及其对于周围建筑物的影响、基坑开挖和水利、农业、环保等许多工程领域均有非常重要的影响[3]。相关学者对于土体的渗透系数进行了大量的试验及理论推导[4-7]，近年来，中外学者从不同角度对黏性土的渗透系数计算方法进行了大量的研究[8]，但由于参数无法从简单的试验中获取，实用性有待提高。梁健伟等[9]对影响黏性土渗流特性的原因及改变渗流特性的重要影响参数进行研究。何俊等[10]从微观角度对土工合成黏土衬垫的饱和渗透系数进行研究。张一军[11]研究了黏性土尾矿坝的稳定性，结果表明黏性土具有渗透性差、易变性、强度低、触变性、非均匀性等特点；唐大雄等[12]总结了黏性土的渗透规律，并提出了达西定律的适用条件；董邑宁等[13]对饱和黏性土进行了大量的渗透试验，揭示了土体只要有水压差就会发生渗流。梁健伟[14]研究发现黏性土中的黏性土颗粒会吸附部分水在其孔隙中，使得黏性土的渗流规律与达西定律有一定的偏差。在油气开采领域中大量学者提出土体三相间是存在相互作用的且渗流液体自身具有物理化学性质和流变性质[15-16]。

黏性土是指粒径小于0.075 mm的土体质量占总质量一半以上的一类土。传统渗透系数经验公式计算黏性土渗透系数常与实测值存在一定偏差。造成这种误差的根本原因是黏性土颗粒粒径较小，在静电力作用下土颗粒外存在结合水膜，而结合水渗透性极差具有类似固体的性质，不会产生渗流。本文结合变水头渗透试验，通过控制黏性土样的干密度研究孔隙度对黏性土渗透系数的影响。对试验数据进行整理分析，拟合黏性土的渗透系数与孔隙比之间的数值关系，并分析了传统渗透系数在计算黏性土时常存在误差的原因。

1 试验土样基本物理指标测定

1.1 颗粒分析

试验所用土体为重塑土，分别为红黏土与黄黏土。烘干后土样如图1所示。采用密度计法对两种黏性土样进行颗分试验，两种黏性土的颗粒分析结果如表1所示，颗粒级配曲线如图2所示。

图1 烘干后土样

由两种黏性土的颗粒级配曲线可知试样使用两种黏性土级配良好，均满足《土工试验规程》SL237—1999的相关土工试验要求。

图2 土样颗粒级配曲线

1.2 比重实验

将两种黏性土样烘干，校正比重瓶，称量15 g土样并将其装入100 mL比重瓶中，并向比重瓶内注入一半蒸馏水，将土样浸泡于比重瓶内24 h，将比重瓶置于砂浴中煮沸。自悬液沸腾时开始计算煮沸时间，两种黏性土煮沸时间均为1 h，令土颗粒均匀分散。冷却后将蒸馏水注入比重瓶至满瓶。比重瓶冷却至室温，擦干比重瓶外壁，对比重瓶、试样及水的总质量进行称量并测量蒸馏水的温度。试验测量数据应精确至0.001 g，两种土样比重试验结果如表2所示。

表1 黄黏土、红黏土颗粒分析结果

表2 两种试验土样的比重

1.3 最大、最小干密度试验

通过最大孔隙比试验及最小孔隙比试验来测定试验所用黏性土样的最大干密度与最小干密度，以设定黏性土样干密度。最大孔隙比试验使用量筒法，最小孔隙比试验使用锤击振动法。两种试验需进行两次平行试验，并取算术平均值作为土样最大及最小干密度，两次平行试验所得结果之差不可超过0.03 g/cm3。两种黏性土最大、最小干密度试验数据如表3所示。

表3 两种黏性土样的基本物理参数

2 渗透试验及结果分析

2.1 土样制备

土样底面直径为39.1 mm，高度为80 mm。根据最大及最小孔隙比试验所测得的土样最大干密度及最小干密度，分别设定两种黏性土的五种土样干密度。计算所需土样质量及配水质量。配水方法为将每组土样所需黏性土等质量分成四份，用滴定管将计算好质量的水均匀滴入土样上方并将土样搅拌均匀，配水结束后，将黏性土试样密封并保存48 h。

将保湿缸中搅拌均匀并静置48 h的土样取出，每种干密度的土样分别分等质量的四份倒入制样器中。每份倒入后均对土样进行击实并在击实后对土样上表面进行刮毛处理，待土样全部放入制样器并压实后抚平土样上表面，如图3所示。在土样的上下表面均贴上滤纸并用透水石进行固定，每个试样上贴好记有试样的土样种类及试样干密度的标签，采用真空饱和法对试样进行饱和处理，如图4所示。

图3 压实后的黏性土样

图4 土样饱和

试样饱和后将试样装入渗透仪器中，如图5所示。施加围压直至试样变形趋于稳定，固结时间不少于6 h。试样固结完成后，分别施加上下水头压力并设置水头压力差为20 kPa，待单位时间内上端流入水体积与下端流出水体积大致相等，根据Darcy定律计算试样的渗透系数：

(1)

式(1)中：kT为试样在温度T时的渗透系数，cm/s；Q为单位时间内流过试样的水体积，cm3/s；A为试样的横截面积，cm2；L为试样高度即渗流长度，cm；h1-h2为上下水头高度差，cm。每个试样分别在渗流稳定之后反复记录6次以上并计算试样渗透系数直至计算结果趋于稳定，同时测量试验开始及结束时的水温。根据式(2)计算标准温度下的试样渗透系数：

(2)

式(2)中：k20为标准室温20 ℃时试样的渗透系数，ηT/η20为T℃时与20 ℃时水的黏滞系数比。

图5 渗透仪器

2.3 渗透试验结果分析

基于渗透试验测试数据，可得到两种黏性土样在不同干密度条件下渗透系数随时间的变化如图6所示。

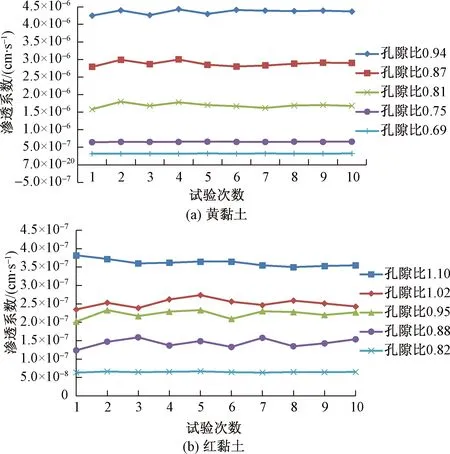
图6 两种黏土在不同孔隙比条件下渗透系数随时间的变化

通过变水头渗透试验所得结果显示黏性土渗透系数随土样干密度增大而减小，即渗透系数随试样孔隙比减小而减小。且由于试验数据具备一定的波动性，经过数次试验之后，试验数据基本趋于稳定，取多次变水头渗透试验所得渗透系数的算术平均值作为最终的渗透系数实测值。基于渗透试验测试数据，可得到两种黏性土不同孔隙比对应渗透系数实测值汇总于表4，渗透系数随土样孔隙比变化的规律如图7所示。

黄黏土及红黏土的渗透系数量级分别是10-6～10-7cm/s、10-7～10-8cm/s。经整理分析，试验所得渗透系数数据具备较强的规律性并基本符合函数拟合曲线。由图7、图8可知，对于同种黏性土，随着孔隙度增大渗透系数也不断增大。可见孔隙比对饱和黏性土的渗透性存在影响，随着孔隙比的增加，渗透系数呈非线性增加，通过数据拟合，可得到黄黏土渗透系数k与孔隙比e间的函数关系式为：

图7 两种黏土渗透系数随试样孔隙比的变化

k=10-7(7 513.3e4-2 6621e3+35 406e2-

20 742e+4 500.2)

(3)

红黏土渗透系数k与孔隙比e之间的函数关系式为

k=10-7(3 442.2e4-12 923e3+18 124e2-

11 245e+2 603.9)

(4)

对于黏性土而言，将黏性土的基本物理参数直接代入传统的渗透系数经验公式中，计算结果往往与实测结果有一定的误差，这说明传统的渗透系数经验公式并不适用于黏性土。造成这一现象的主要原因是黏性土内部土颗粒粒径相对较小、比表面积大、分子间引力较大、土体中所包含的细颗粒含量较高、并且黏性土颗粒具有带电性质，黏性土土颗粒表面会吸附一层结合水膜。而黏性土内部结合水由于黏滞性大，透水性差且不受重力影响，具有类似于固体的性质，造成这部分孔隙基本是不能产生渗流。传统的渗透系数经验公式并未考虑这一部分无效渗透孔隙，因此在计算黏性土时往往会使得计算值大于实际渗透系数，通过对不同孔隙比的黏性土试样进行渗透试验并拟合出黏性土孔隙比与渗透系数之间的函数关系，进一步完善了黏性土渗透性理论，为实际工程提供了一定的借鉴和参考。