一类双调和方程边值问题的正径向解研究

钟金标, 方 兴, 王 花

(安庆师范大学 数学与计算科学学院,安徽 安庆 246133)

0 引 言

源于流体力学与固体力学等物理问题建立的多调和方程边值问题一直是偏微分方程领域重要研究问题之一。文献[1]利用Schaude-Tychonoff不动点定理证明了一类R2上奇异非线性双调和方程正径向解的存在定理,并讨论了解的部分性质;文献[2]利用变分方法研究了一类带有双临界指数的双调和方程边值问题的非平凡解;文献[3]通过建立一个嵌入定理,结合山路引理证明了一类渐近线性双调和问题非平凡解的存在性;文献[4]利用Schaefer不动点定理证明了半线性双调和问题解的存在性与唯一性,该问题为:

文献[5]利用上下解方法、不动点定理在洞型区域内研究了一类双调和方程边值问题弱解的存在性,该问题为:

其中,Γ1、Γ2为区域Ω的内、外边界。

文献[1-5]分别对双调和方程的不同类型探讨了解的存在性;文献[6]讨论了半线性椭圆型方程组边值问题解的存在性、唯一性,该问题为:

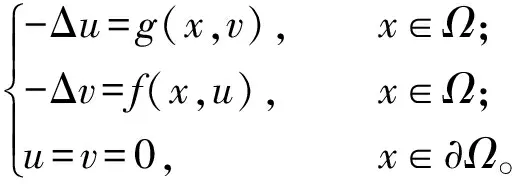
本文考察双调和边值问题:

(1)

其中,B为球心在坐标原点的单位球,B∈Rn。

本文通过变量代换将双调和边值问题(1)式转换为椭圆型方程组边值问题,再利用不动点定理讨论正径向有界解的存在性。文献[1]中研究的问题是在R2区域上进行的;本文是在Rn区域中球心在原点的单位球上讨论的。本文问题(1)中非线性项函数与文献[1]中问题的非线性项满足的条件不同,2个问题所属类型不同,证明相应定理使用的方法也不同;与文献[2-5]所研究的方法、所证解的类型及非线性项范围也不同。

在(1)式中，令-Δu=v，则(1)式转化为方程组问题:

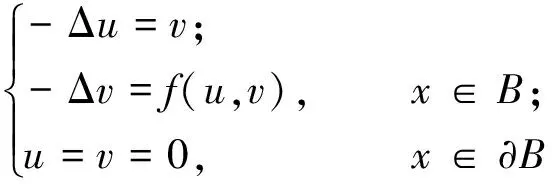
(2)

(2)式的径向形式为:

(3)

给定如下假设条件H1、H2。

H1：f(s,t)关于s与t是连续单增的,且f(s,t)≥0。

1 解的存在性

定理1 若H1成立,则若(2)式有解,必是正解。

证明因为f(u,v)≥0,x∈B,所以有:

-Δv≥0,x∈B。

由上调和函数极值原理可知:v≥0,x∈B。

又因为-Δu=v≥0,再利用上调和函数极值原理知u≥0,从而(2)式的解为正解。

定理2 假定H1、H2成立,则(3)式的解必有界。

证明由(3)式中方程可得:

则有:

(4)

由H1知v′(r)≤0,因此v(r)单减。因为

所以u(r)单减。

因此

rv(r)≤-nu′(r)。

因为u′(0)=0,u′(r)连续,所以存在r1∈(0,1),使得:

|nu′(r)|<1,r∈(0,r1]

(5)

由(3)式有:

因为v′(0)=0,v′(r)连续,所以存在r2∈(0,1]，使得:

|nv′(r)|≤1，r∈(0,r2]

(6)

取r0=min{r1,r2}，则当r∈(0,r0]时,(5)式、(6)式同时成立,即

|rf(u(r),v(r))|<1,

|rv(r)|<1，r∈(0,r0]。

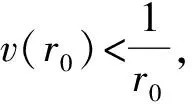
因为

所以

v(0)=v(r0)+

故v(0)有限。又因为

所以u(0)有限。

由u(r)与v(r)的单减性,结合定理1可知,(3)式若有解必为有界正解。

引理1[7](不动点定理) 设X是一个Banach空间,B是X的一个闭凸子集。若T是B到B的一个紧映射,R为一个正常数,使对满足‖V‖=R的任意V∈B,有V≠tT(V)(0≤t≤1),则T有1个不动点V∈B且‖V‖≤R。

定理3 设H1、H2成立,则(3)式存在1个有界的正径向解。

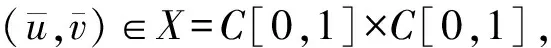
(7)

设B={(u,v)|(u,v)∈X且u(1)=v(1)=0,u′(0)=v′(0)=0},则B是X的一个闭凸子集,且T:B→B是全连续的[8]。取常数R=τ>0充分小。

下面证明对满足‖(u,v)‖∞=R=τ>0的任意(u,v)∈B,有(u,v)≠tT(u,v)(0≤t≤1),并且有：

‖(u,v)‖∞=max{‖u‖∞,‖v‖∞}，

假设存在(u,v)∈B,使得(u,v)=tT(u,v),则有:

从而有:

(1) 若‖(u,v)‖∞=τ=‖u‖∞，则有:

矛盾。

(2) 若‖(u,v)‖∞=τ=‖v‖∞,则由H2知，当τ充分小时,有

τ=‖v‖∞=

矛盾。

因此,由引理1知，T有1个不动点且有界,该不动点即为(3)式的有界正径向解。

例1 考察问题:

(8)

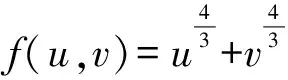
即

因此，f(s,t)满足H1、H2。由定理3知，(8)式存在1个有界正径向解。

2 解的唯一性

一般双调和方程边值问题或非线性方程组解的唯一性不易得到,通常需要在保证解存在性条件下,通过附加适当条件得到解的唯一性。

给定以下假设条件H3。

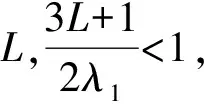
定理4 若H3成立,则(2)式的解唯一。

证明设(u1,v1)、(u2,v2)为(2)式的2组解,则有:

从而有:

-Δ(u1-u2)=v1-v2

(9)

-Δ(v1-v2)=f(u1,v1)-f(u2,v2)

(10)

在(9)式两边乘以(u1-u2)、(10)式两边乘以(v1-v2)后在Ω内积分,并利用Green恒等式与Poincare不等式可得:

(11)

(12)

(11)式、(12)式相加可得:

u1=u2,v1=v2。

因此,(2)式解唯一。