基于灰色马尔科夫模型的沥青磨耗层长期性能预测

柳子晖, 李 颖， 聂 文, 熊春龙

(1.广州北环高速公路有限公司,广东 广州 510507; 2.广州肖宁道路工程技术研究事务所有限公司,广东 广州 510641)

0 引 言

随着车辆荷载与气候环境因素的作用,路面结构在运营过程中不可避免地会出现坑槽、开裂和抗滑性能不足等病害。薄层罩面作为一种预防性养护技术,在延长路面的使用寿命、改善道路行驶质量、修补道路表面缺陷、提高行车安全特性(包括提高抗滑与排水)及降低行驶噪音等方面具有良好的效果,因而得到了广泛应用[1-2]。

目前,雾封层、微表处和NovaChip超薄磨耗层等各类薄层罩面养护技术在公路养护项目中得以较大规模地实施和应用,一定程度上达到了延缓路面大中修期限、节约养护成本的技术目的[3-5]。然而,也有部分工程同样实施了薄层罩面却未能达到预期的养护效果,出现了罩面性能衰减过快、寿命低于预期等问题。各类薄层罩面的使用寿命与长期性能变化规律目前尚未形成统一的认知,因此,基于现有薄层罩面性能变化规律,寻找一种科学有效的性能预测模型,预估各类薄层罩面的长期性能,为公路养护部门的决策提供依据迫在眉睫。

薄层罩面的性能变化受自然条件、社会环境及人为因素等多方面的影响,表现出一定的随机性和动态性。灰色马尔科夫模型的特点是在预测变化趋势较为明显的时间序列中针对随机变化的系统具有比较好的预测性能,且精度较高,这为薄层罩面使用性能的预测提供了一种新的有效方法[6]。本文根据广东某高速公路水泥混凝土桥面板上采用的3种不同类型薄层罩面跟踪观测数据,采用灰色马尔科夫模型对其进行长期性能预测,以期为寻找科学有效的薄层罩面寿命预估模型提供参考。

1 灰色马尔科夫理论

1.1 GM(1,1)模型

在灰色系统理论中,根据系统信息已知程度的不同将系统分为3种,分别是白色系统、灰色系统、 黑色系统。若系统的信息均已知,则将该系统称为“白色系统”;若系统信息部分已知、部分未知,则将该系统称为“灰色系统”; 若系统信息均为未知,则将该系统称为“黑色系统”。对于薄层罩面使用性能预测问题,系统信息包含薄层罩面使用性能的历史资料、交通荷载因素、环境影响因素、人为因素等诸多信息，该系统信息部分已知、部分未知,构成了一个较为复杂的灰色系统,因此薄层罩面使用性能的预测问题可以采用灰色系统理论来进行求解[7-8]。

灰色系统理论建模的基本思想是:将白色信息序列按照一定规律组成动态、非动态的白色模块,再通过一定的算法求解将来的灰色模型。灰色模型的求解过程是一个系统白度不断提高的过程,随着系统白度不断提高,其发展变化规律也会逐渐显现。灰色理论模型是建立在把离散的时间序列拟合为一阶线性微分方程基础之上的。GM(1,1)模型的变量只有1个,较为简单,容易被人们理解和接受,在灰色系统理论的预测模型中是应用得比较广泛的一种。在建模过程中,GM(1,1)模型并不是对系统中的所有因素进行分析拟合,而是对系统中的主要因素进行分析拟合并预测,以生成的函数作为预测的基础。GM(1,1)模型所采用的建模数据是通过累加变换得到的新的数据序列,而不是所收集的原始历史数据序列。具体建模过程和运算步骤如下。

收集历史资料构造原始数据序列,即

X(0)={X(0)(1),X(0)(2),…,X(0)(n)}

(1)

处理原始数据序列X(0)得到数据序列X(1):

X(1)={X(1)(1),X(1)(2),…,X(1)(n)}

(2)

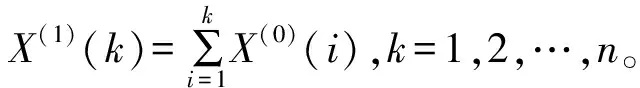
原始数据通常会有一定的波动性和随机性,这样的数据不利于模型的建立,这里采用累加处理的方式来解决此问题。在生成序列的基础上求解得到生成函数,据此建立被研究对象的模型。建立新数据序列的GM(1,1)模型,通过线性拟合得到一阶白化方程,再进一步求解就可以得到模型的预测值。

(3)

其中,a、m为待求解的系数。

[am]T=(NTN)-1NTM,

M=[X(0)(2)X(0)(3) …X(0)(n)]T,

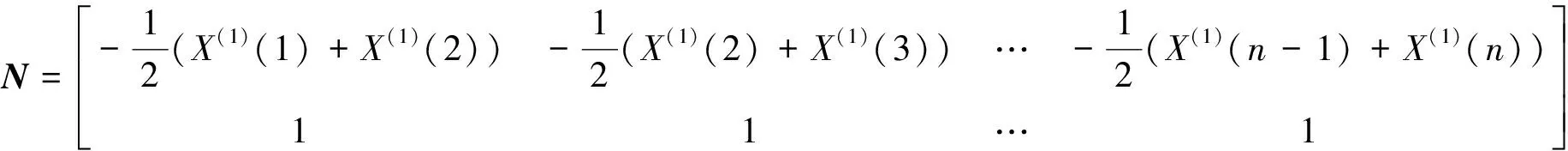
(4)

1.2 马尔科夫模型

马尔科夫预测模型是一种随机的、变化的数学过程,建模的核心在于掌握系统状态转移规律。马尔科夫概率预测模型的基本思想是分析研究系统现状,利用马尔科夫链求解得出系统将来可能变化所至的某特定状态的概率[9-10]。因为该数学过程有一定的随机离散特性,所以需要采用数学概率来定量表述系统状态转移的可能性大小。

定义St为系统在时刻t所处的状态,若在t=i时刻的状态Si为已知,则在未来的某个t=i+1时刻系统所能达到的某种状态Si+1只与t=i时刻的状态Si有关,而与之前的状态没有关系,即马尔科夫链可以看成是一种无后效性的离散随机过程。定义Pij为系统由状态Si经过1次转移到状态Sj的概率,当系统存在n种状态,把这些状态组合在一起后所构成的矩阵P称为状态转移矩阵，即

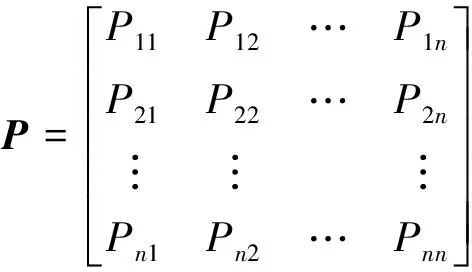
(5)

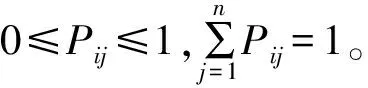
1.3 灰色马尔科夫模型

(1) 通过对收集的已知历史数据的处理,将累加得到的数据序列代入GM(1,1)模型,求解模型可以得到系统的灰色预测值：

(6)

(2) GM(1,1)模型的计算结果可能与已知的实际值不一致,即可能存在一定的偏差,定义偏差的数值为残差Q,残差和实际值的比值为残差比率q，即

(7)

(8)

(3) 根据残差数值的正负情况和数值的大小划分若干状态区间,y:[lg,lh],其中y表示所划分的残差状态区间,lg、lh分别为所对应的状态区间上、下限。

(4) 通过马尔科夫模型计算残差转移矩阵,残差状态转移概率计算公式为:

(9)

其中,nijC为残差状态yi经过1次转移到残差状态yj所出现的次数;ni C为残差状态yi发生状态转移的次数。PijC所构成的残差状态转移矩阵PC为：

(10)

确定残差状态转移矩阵后,根据系统的初始状态可以得出未来某个预测时间点的残差状态,即可以按一定的概率确定由之前GM(1,1)模型所得预测值的偏差。

(11)

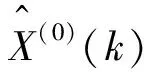
2 薄层罩面使用性能的预测

2.1 预测指标的选取

通过对广东某高速公路水泥混凝土桥面板上使用的微表处、高黏度乳化沥青(high-viscosity emulsified asphalt,HVE)超黏磨耗层、NovaChip超薄磨耗层3种养护技术进行不同时期的性能跟踪检测,现场发现薄层罩面表面沥青及集料的磨耗较为明显,且部分路段有轻微辙痕,考虑到广东省地处亚热带季风气候,常年高温,以此确定了对薄层罩面使用性能影响最大的2个指标,即表面摩擦系数和车辙深度[11-15]。现场薄层罩面表面抗滑衰减和辙痕情形如图1所示。

图1 现场薄层罩面表面抗滑衰减和辙痕情形

2.2 GM(1,1)模型

收集广东省某高速公路2016—2019年的水泥混凝土桥面上的薄层罩面使用性能数据,选取摩擦系数值和车辙深度值分别作为原始数据序列,其中以2016—2018年的摩擦系数和车辙深度数据作为建模数据,2019年摩擦系数和车辙深度数据作为检验模型优劣的标准。2016—2018年广东某高速公路薄层罩面摩擦系数BPN值和车辙深度数据分别如图2、图3所示。

图2 摩擦系数BPN值历史数据

图3 车辙深度历史数据

以NovaChip超薄磨耗层罩面为例,运用Matlab进行计算,得到的计算结果分别为:

因此,摩擦系数和车辙深度指标GM(1,1)模型的时间响应序列分别为:

本次研究中的相关数据需接受SPSS21.0软件包分析,患者计数资料为n(%),并接受X2检验,患者计量资料需要利用(±s),并利用t值进行验算。若两组患者数据比较后结果显示P<0.05,即为存在明显意义。

计算得到摩擦系数、车辙深度原始数列的预测值分别为:

由各年份摩擦系数和车辙深度预测值的计算结果可得到各年份的摩擦系数和车辙深度预测值以及所对应的Q、q残差比率,通过马尔科夫链对预测结果进行进一步的修正。

2.3 用马尔科夫链修正预测值

根据GM(1,1)模型预测值和摩擦系数、车辙深度实际值的相对误差大小以及符号的不同,可以将残差划分为3种不同的状态,见表1所列。NovaChip超薄磨耗层摩擦系数预测值、Q及所属状态见表2所列,车辙深度预测值、Q及所属状态见表3所列。

表1 残差状态分布

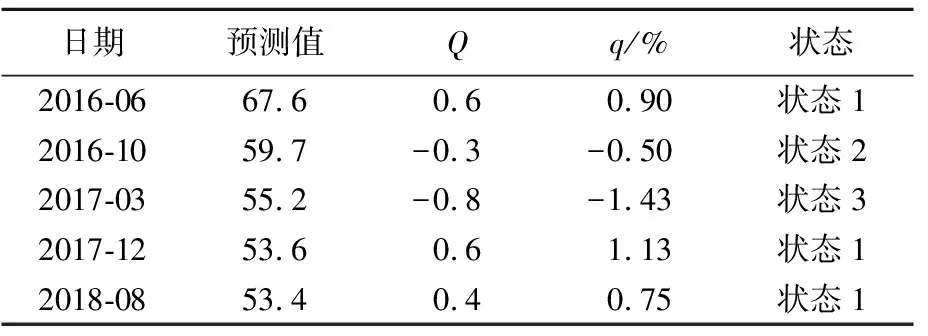
表2 NovaChip超薄磨耗层摩擦系数预测值、Q及所属状态

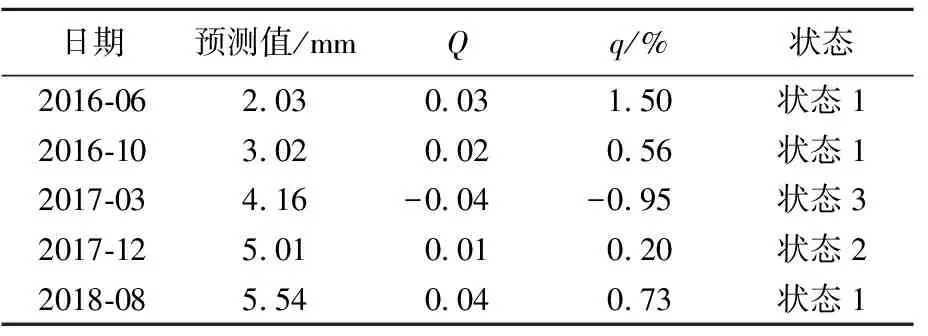
表3 NovaChip超薄磨耗层车辙深度预测值、Q及所属状态

残差的状态有3种,不同年份的残差状态有不同的转移规律,nijC结果见表4所列。

表4 残差状态转移nijC结果

根据表4，相应的1次转移残差状态转移矩阵为:

当系统满足稳定性假设时，s次状态转移矩阵的计算公式为：

l=1,2,…,s。

由此可得2、3次状态转移矩阵分别为：

由表2、表3可知,摩擦系数和车辙深度在2018年8月都处于状态1,因此确定2019年GM(1,1)模型预测值的残差状态时,考虑选择(P(1))2第1行所对应的状态转移向量作为2019年残差状态转移向量。2019年GM(1,1)模型预测值残差状态转移向量中概率最大值见表5所列。

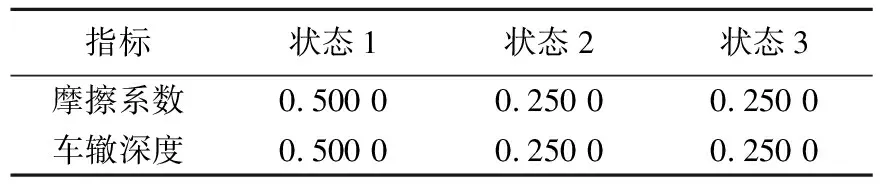
表5 2019年预测值残差状态转移向量最大概率值

注：表中为NovaChip超薄磨耗层的结果。

由表5可知,2019年摩擦系数和车辙深度的GM(1,1)模型预测值残差处于3种状态的概率是不一样的,2019年预测值残差所对应的状态向量中,残差状态处于状态1的概率最大为0.5,因此选择状态1所对应的误差区间[0.5%,1.5%]的中值1.0%对GM(1,1)模型预测值进行修正,修正方式按(11)式,修正后得到的2019年NovaChip超薄磨耗层罩面摩擦系数预测值为52.9,车辙深度预测值为5.51 mm。灰色马尔科夫模型2019年的预测结果见表6所列。

表6 NovaChip超薄磨耗层2019年预测结果

注:车辙深度单位为mm。

同理,可计算得到微表处、HVE超黏磨耗层灰色马尔科夫模型2019年的预测结果,见表7所列。

表7 微表处、HVE超黏磨耗层 2019年预测结果

注:车辙深度单位为mm。

从表6可以看出,灰色马尔科夫预测模型下的NovaChip超薄磨耗层摩擦系数与车辙深度的q值均较小,两者预测结果均为“状态2”。由表7可知,不论是微表处还是HVE超黏磨耗层,马尔科夫预测模型下的摩擦系数与车辙深度预测结果均较为准确。由此可见,马尔科夫预测模型的准确度和精度都较高。

2.4 不同养护措施长期性能预测结果

应用马尔科夫预测模型,对3种薄层罩面类型的长期使用性能进行预测,以获得不同薄层罩面长期路用性能的发展及衰变规律,预测结果如图4、图5所示。

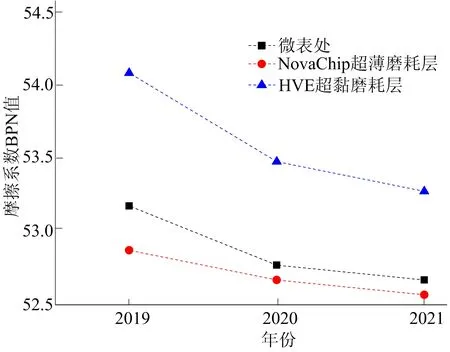
图4 不同薄层罩面摩擦系数预测结果

图5 不同薄层罩面车辙深度预测结果

由图4可知,不同薄层罩面的摩擦系数即抗滑性能在2019—2020年有较为明显的下降,在2020—2021年,3种薄层罩面的摩擦系数下降趋势开始放缓,逐渐趋于平稳。由图5可知,不同薄层罩面的车辙深度均随着时间增加呈现较为明显的增长,且2020—2021年的增长幅度明显要大于2019—2020年。

从以往几年的实测数据及长期使用性能预测结果看,NovaChip超薄磨耗层抗滑性能最为稳定,随着时间的增长下降幅度最小,长远来看,在抗滑性能上NovaChip超薄磨耗层比微表处和HVE超黏磨耗层更有优势。此外,可以明显发现,NovaChip超薄磨耗层的车辙深度最小,且随着时间增加其车辙深度也没有出现较为剧烈的增长,而微表处的车辙深度一直较大,且增长趋势较明显,由此可见,NovaChip超薄磨耗层具有较好的抗车辙能力,微表处抗车辙能力较差。

3 结 论

本文运用灰色马尔科夫链路面使用性能预测模型,对广东省某高速公路水泥混凝土桥面上使用的3种养护技术(微表处、HVE超黏磨耗层、NovaChip超薄磨耗层)的摩擦系数与车辙深度指标进行了预测分析,得出如下结论:

(1) 路面使用性能的预测受到各方面不同因素的影响,具有随机性和波动性。在具有一定历史数据的条件下,通过建立灰色马尔科夫模型,借助Matlab计算求解,验证了该模型能够达到比较高的预测精度。

(2) 灰色马尔科夫模型是基于马尔科夫链对灰色模型进行修正,实例表明经过马尔科夫链修正后的预测结果准确度较高,实用性较强。

(3) 在实际工程中,采用灰色马尔科夫模型对高速公路水泥混凝土桥面板上薄层罩面的使用性能进行预测是可行的,本文虽然以摩擦系数和车辙深度预测为例,但也适用于薄层罩面路用性能其他指标的预测。实例证明这一模型具有较高的应用价值。

(4) NovaChip超薄磨耗层抗滑性能最稳定,随时间下降程度最小,在后期抗滑性能与HVE超黏磨耗层和微表处相比具有较大优势;NovaChip超薄磨耗层车辙深度最小,具有较好的抗车辙能力,微表处抗车辙能力较差。