随机缺失函数型数据的k近邻估计及其应用
2020-04-08程彦茹凌能祥
程彦茹, 凌能祥
(合肥工业大学 数学学院,安徽 合肥 230601)
考虑函数型数据非参数回归模型:
Y=m(χ)+ε
(1)
其中,Y为响应变量(标量);χ为取值于无限维向量空间SH⊂H中的函数型解释变量;m(·)为从SH到R的未知回归算子;ε为随机误差,且满足:
E(ε|χ)=0,a.s.;0 文献[1]提出的函数型非参数回归算子的k近邻估计量,用交叉验证寻找最优的正整数k来代替传统NW核回归估计中的连续窗宽h,更符合函数型数据的局部结构,相关文献可参见文献[2-5]。 考虑到实际中观测手段、天气状况及仪器设备等影响,收集的数据常常是不完全的,响应变量随机缺失就是一种常见的情形。因此本文主要研究响应变量Y随机缺失时非参数回归模型(1)的k近邻估计,即当Y缺失时,δ=0;反之δ=1,并且满足给定χ时,δ与Y是条件独立的,即P(δ=1|Y,χ)=P(δ=1|χ)=p(χ),a.s.。 假设随机向量{(χi,δi,Yi)|1≤i≤n}来自总体(χ,δ,Y),Yi缺失时,δi=0;反之δi=1。则Yi=m(χi)+εi,i=1, 2,…,n。m(·)的k近邻回归估计定义如下: (2) 其中,K(·)为实值核函数;d(·,·)为空间H上的半度量;Hn,k(χ)为随机窗宽,满足: 其中,B(χ,h)为以χ为中心,h>0为半径的小球。若Hn,k(χ)=hn(χ),其中hn(χ)为一列非随机正序列,且随着n→∞时,趋近于0,则(2)式转化为文献[6]提出的NW核估计量,即 (3) 为了通过熵的概念来证明H的子集SH上的一致结果,给出空间SH上Kolmogorovε熵的定义为ψSH(ε)=log(Nε(SH)),其中Nε(SH)为在空间H上必须覆盖SH的开球半径ε的最小值。 由于篇幅有限,一些前提假设可见文献[4]中假设H1~H6。以下是估计量的渐近性质。 (4) 为证明定理1,需要如下2个引理。类似于文献[4],令{(Ai,Bi)|1≤i≤n}为取值于(Ω×R,A×(R))的随机向量,其中(Ω,A)为通常的可测空间。令SΩ为Ω的固定子集,G(·,·):R×(SΩ×Ω)→R+为函数,且∀χ∈SΩ,G(·, (χ,·))为可测的。同时对∀t,t′∈R,t G(t,z)≤G(t′,z), ∀z∈SΩ×Ω。 对于∀χ∈SΩ,n≥1,定义: (2) 当n→∞时,有 O(un)。 则有: (5) 证明见文献[4]。 引理2 在文献[4]假设H1~H6下,有 (6) 证明见文献[7]。 下面在引理1、引理2的基础上给出定理1的证明。 严格意义上讲,甲状腺结节性病变从其发病特点上区分,可分为两类。第一类,单发性结节;第二类,多发性结节。在临床诊断治疗领域,需要密切关注的是病变性的结节特征。具体来看,包括结节的大小、部位、质地、功能等。如上所述,甲状腺结节病变主要呈现为单发性和多发性,包括有增生性、肿瘤性、胶体性、囊性、甲状腺炎性等。总之,在临床治疗尤其是早期控制阶段,对不同类型的甲状腺结节性病变予以对应的治疗措施是非常关键的。正如开篇所言,B超检查诊断的临床意义巨大。 本节通过模拟研究来验证k近邻回归估计 的有效性,同时在有限样本下将本文提出的k近邻回归估计与文献[7]提出的NW核回归估计的预测效果进行对比。 t∈[0, π], n=200的曲线样本如图1所示。同时,取核函数为K(u)=1-u2,u∈(0,1),半度量为: ∀χi,χj∈SH。 图1 n=200的曲线样本 其中,MSEj为第j个检验样本的MSE,具体结果见表1所列。本文缺失机制同文献[8],α越大,缺失率越小。 从表1可以看出,在相同样本量下,2种估计量的AMSE都随着缺失率的减小(α增大)而逐渐减小;在缺失率相同的情况下,样本量越大,2种估计量的预测效果越好;而在样本量与缺失率均相同的前提下,k近邻估计量的预测效果比NW核估计量的预测效果好。表中数据说明,k近邻估计量可以较好地处理缺失数据的预测问题;结合文献[1,2,9]的结论,可以发现在任何情况下,k近邻估计量与NW核估计量相比有明显的优势。 表1 2种估计量在不同样本量和缺失率下预测的AMSE 图2 N=781条温度曲线 图3 不同缺失率下的预测结果 理论验证k近邻估计的合理性后,模拟实验以及真实数据分析都展示了k近邻估计在函数型数据为解释变量,响应变量随机缺失时的预测能力,与NW核估计相比,k近邻估计不仅预测效果更好,同时也考虑到了数据的局部性质,为函数型数据在实际生活中的应用提供了更广阔的平台。1 估计量的构造及主要结果
1.1 模型及估计
1.2 主要结果

2 引理及定理证明

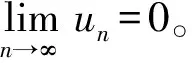


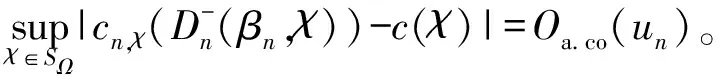

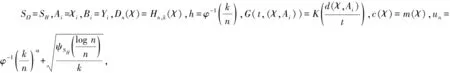
3 模拟研究




4 真实数据分析
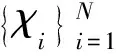
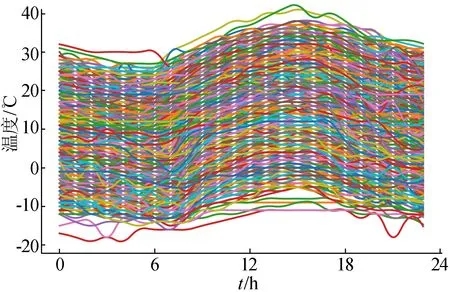
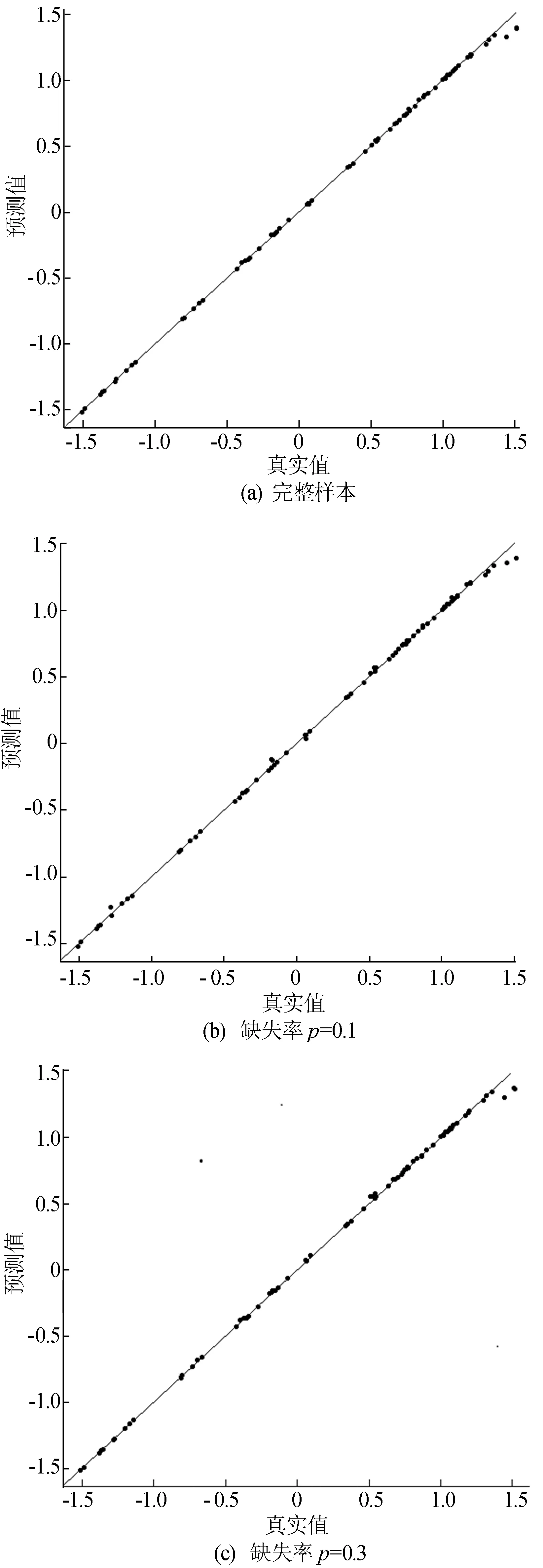
5 结 论
