趣题引领探究乐 师生共研有惊喜

广州大学附属中学(510006) 朱惊涛

数学问题有好的问题和不好的问题之分,好的数学问题应有利于学生巩固数学核心知识,训练数学基本方法,领悟数学基本思想,激活数学直觉思维和逻辑思维[1].教师应有意识的选择或提出好的数学问题作为学生探究的对象,不仅可以发展学生的核心素养,也能够提高自身的专业水平.以下是笔者在高三教学中遇到的一道有趣的题,并围绕它,师生共同开展探究的历程.

1 由一道题引起的推广、证明及猜想

在一次套卷练习中,师生遇到这样一道题:

问题1(河南省洛阳市2017 届高三第三次统一考试数学文科) 如图1,四边形ABCD为直角梯形,∠ABC=90°,AD//BC,AB=,AD=10,BC=20 若AB边上存在一点P,使得∠DPC最大,则AP=______.

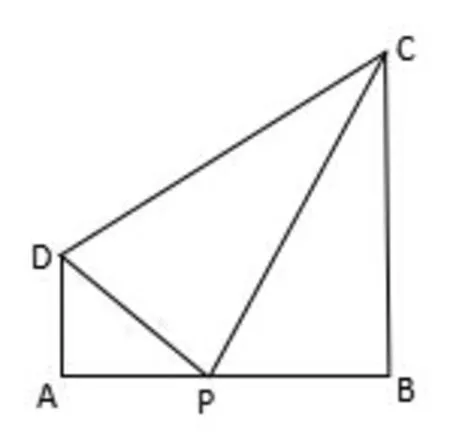
图1

其解法之一如下：以A为坐标原点,直线AB为x轴,直线AD为y轴建立直角坐标系,设点则因为所以∠DPC ∈(0,90°],当时,∠DPC=90°达到最大,所以

笔者反思此题的设计十分凑巧,若∠DPC可以是钝角,又该如何解决?有感此问题的有趣,笔者对问题1 进行了推广研究,把条件简单改变后得到以下问题：

问题2如图2,四边形ABCD为直角梯形,∠ABC=90°,AD//BC,AD=1,BC=2,AB=3,若AB边上存在一点P,使得∠DPC最大,则AP=______.

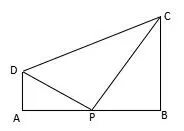
图2

以下是笔者对该题的初步思考：

解由问题1,用同样方法建系,设P(x,0),0≤x ≤3,则①.易知当x=1 或x=2 时,cos ∠DPC=0,∠DPC=90°;1＜ x＜2时,cos ∠DPC＜0,∠DPC为钝角,故为使∠DPC最大,x应在1 到2 之间.但要求①式的最值不容易,例如用求导法就过于复杂.

考虑到此题颇有意义且会对学生构成挑战,笔者在班上开展了一次有奖征答活动,宣布对第一个解出来的同学奖励10 元,第二到第五个奖励5 元,于是同学们跃跃欲试.让我没想到的是,第二天就有4 个同学做出答案,解法各有可观,令笔者颇是惊喜.

其中有3 人的解法皆逻辑严谨,能自圆其说.另一名同学则是通过一个猜想意外获得了答案.笔者让4 位同学分别上台讲解自己的做法.试将各人想法摘录如下：

甲:设AP=x,则PB=3-x,设∠APD=α,∠CPB=β,则tan ∠DPC=tan[π-(α+β)]=-tan(α+β),此时求∠DPC最大值可以转化为求tan(α+β)的最小值.而如前所述,∠DPC最大为钝角,则α+β为锐角,故tan(α+β)＞0,故1＜x＜2,②式取倒数则显然当时③式有最大值,从而②式有最小值,解之即得又因为1＜x＜2,故

点评该生巧妙地利用正切函数,把求∠DPC的最大值转化为求tan(∠DPA+∠CPB) 的最小值,从而得到②式,再求最值就简单了.

乙:如前所述建立直角坐标系,设点P(m,0),0≤m ≤3,则设∠DPC=θ,可得而又m2-3m+2,即(0≤m ≤3),θ最大时为钝角,此时tanθ＜0,故1＜m＜2,以下步骤同甲相似,略.

点评该生方法虽无甲简练,却能综合运用多个知识点,特别是用了数量积的两种表达方式(定义表达与坐标表达)的等价性,成功地把问题转化为易求解问题.

丙:如前所述建系后设P(m,0),设∠DPC=θ,则利用平面两直线的夹角公式原理,则以下步骤同甲乙相似,略.

点评该生利用的平面两直线的夹角公式已非现在教材上的内容,笔者曾经在课堂上补充过一次而已,但这位学生不仅记住了,而且学会了活用.事实上,该公式证明理解起来并不困难.我们作为教师,不能书上有的才讲,书上没有的就不讲.丁:该生没有能给出严谨的解法,但她凭着对问题的满腔热情,经过一整晚的钻研,发现了一个可贵的猜想.

如图3所示：分别延长CD和BA交于点E,则当∠DPC达到最大时,猜想有∠EDP=∠EPC,即ΔEDP∽ΔEPC.利用该猜想,设AP=x,易得EA=3,EP=3+x,ED=CD=由ΔEDP∽ΔEPC.即得即解之即得

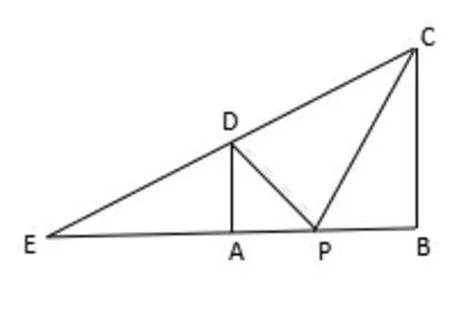
图3

该生用同样方法去解问题1,答案也是正确的,但该生却没能严格证明该猜想的合理性,虽然如此,但这个猜想确实很难得,而且很可能是正确的.

笔者大力表扬和肯定了丁同学的表现.事实上,丁同学的数学学习成绩在班上是中等.但却对新鲜事物很感兴趣(有好奇心),不惜花上一整晚去研究以至耽误了其他科的作业,最终得到了一个令人耳目一新的猜想.不禁让笔者感慨,我们的很多优秀生解题能力很强,但却满足于考试考出好成绩,拿高分.缺乏强烈的好奇心,缺乏对问题深入探究的兴趣.学生如此,老师如此,这不正是当前高中教学中学生练多悟少的弊病所在吗？长期以往,学生创造力如何能够提升？

2 学生猜想的证明

笔者对丁同学的猜想很感兴趣,一度让其他同学尝试去证明,可惜没有同学能说明为什么.笔者经过研究,发现问题其实不难证明.

3 学生猜想的推广和证明

有感于丁同学的猜想能快速简便地解决这一类问题,笔者对该型问题进行了一般化推广.

问题3如图4,四边形ABCD为直角梯形,∠ABC=90°,CB//DA,CB ＞AD,点P为AB边上一动点,分别延长CD和BA交于点E,证明：当∠DPC最大时,有△EDP∽ΔEPC.

图4

笔者对该问题证明如下:

不妨设AD=a,AB=b,BC=c.设AP=x,由相似比可得EA=进而ED=又

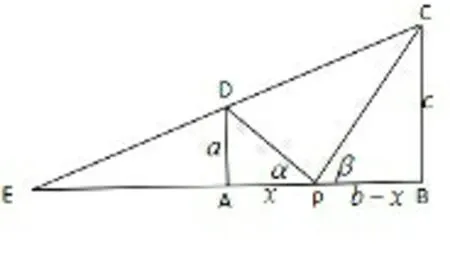
图5

为证ΔEDP∽ΔEPC,等价于证,即EP2=ED·EC,即整理得[ab+(c-a)x]2=ac(c-a)2+b2④,

又设∠APD=α,∠CPB=β.

情形1若∠DPC最大值为钝角或锐角时,tan(α+β)取到最小值时有意义.tan(α+β)=上式可整理为即形如的形式,当上式为正数时,为使其值最小,则最大,即最小,当上式为负数时,为使其值最小,则最大,则最小,同样是最小,综上可知当t2=P,即时上式有最小值,即(易证该式恒有唯一正数解),显然与④式相符.

情形2若∠DPC最大值为直角,则可知存在唯一的一个点P,恰使∠DPC=90°,此时α+β=90°,故成立且只有唯一解(因为点P唯一),整理得x2-bx+ac=0,所以Δ=b2-4ac=0,且将和b2=4ac代入④式,左边=[ab+(c-a)x]2=ac(a+c)2=ac[(c-a)2+b2]=右边,符合④式,命题得证.

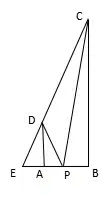
图6

笔者将问题3 抛出,鼓励有兴趣的同学去证明该结论.第二天,收到一位同学的手写证明过程,该同学不仅证明基本无误,他还注意到了一个细节.即当且仅当条件a2b2≤ac[(c-a)2+b2]≤b2c2满足时,才能使[ab+(c-a)x]2=ac[(c-a)2+b2]④式的解落在区间[0,b]上,从而才能在线段AB上找到点P使ΔEDP∽ΔEPC(问题3 的条件是点P在线段AB上).经过与这位同学的交流和探讨,笔者发现自己问题3 的条件设计是有漏洞的,事实上,因为笔者在条件中规定了点P在线段AB上,所以0≤x ≤b,即有ab ≤ab+(c-a)x ≤bc,从而a2b2≤ac[(c-a)2+b2]≤b2c2,也就是学生是正确的！笔者研究发现该不等式左边恒成立(因为c ＞a),右边整理后可以简化为ac-a2≤b2,即ac ≤a2+b2⑤.

例如,当a=1,c=3,b=1 时不满足条件⑤,此时④式的解不落在区间[0,b]上,如图6,在线段AB上不能找到点P,使得ΔEDP∽ΔEPC,这是因为此时∠EDP为锐角,而∠EDP为钝角,故∠EDP /=∠EPC.

不过在上述情况下,可以令点P右移取在AB的延长线上,则可以找到一个位置使得∠EDP=∠EPC,进而ΔEDP∽ΔEPC.事实上,∠DPC最大时,即 ④式要成立,条件a2b2≤ac[(c-a)2+b2]≤b2c2是为了保证④式的解符合0≤x ≤b,准确的说,是使得x ≤b,如果不要求x ≤b,则并不需要条件⑤,因为④式可解得唯一正数解可能小于等于b,也可能大于b,这说明符合ΔEDP∽ΔEPC的点必然存在射线AB上且是唯一的.且当∠DPC最大时必有ΔEDP∽ΔEPC.

至此为使问题3 的结论无误,应该增加条件“AD·BC ≤AD2+AB2”,方可在线段上AB存在点P,使得当∠DPC最大时,有ΔEDP∽ΔEPC.又或者不增加条件,即干脆把“点P为边AB上一动点”改为“点P为射线AB上一动点”即可.

回顾这一题的探究历程,最让人感到欣喜的是丁同学的猜想,这启示我们在教学中应致力于开展好的问题的探究活动,激发学生的好奇心和求知欲,同时引导学生多悟,多反思,鼓励坚持不懈、努力专研的探索精神,鼓励创新和发现,助力学生核心素养的提升.