一种基于改进RRT*的移动机器人的路径规划算法
2020-04-08宋林忆严华
宋林忆,严华
(四川大学电子信息学院,成都 610065)
0 引言
随着人类科技的不断发展与进步,移动机器人越来越多地被运用到我们的工作当中。路径规划算法[1]的研究是当前机器人研究的一个重要分支,它指移动机器人在当前地图中能够找出一条合适的从起点到终点的轨迹,并且能够绕过障碍物。
目前已有许多成熟的理论,如势场法[2]、A*算法[3]和遗传算法[4]等,快速探索随机树算法(RRT)[5]亦是其中之一。RRT算法效率高并且可以运用于未知地图中,然而RRT算法依旧存在着一些不足,如生成的路径成本高而不优,路径要在全地图中来搜索和采样,从而增加了很多不相关节点,增加了存储器需要的内存,并且所需时间相应增长,收敛速率缓慢[6]。
由于上述不足的存在,国际上很多学者纷纷对这些进行了研究,并提出了很多改善后的RRT算法,以适应不同的应用场景。Kuffne和Lavalle联合发表了RRT-connect算法[7],第二年,提出了一种双向搜索树[8]。C.Urmson和R.Simmon发表了一个基于启发式的偏向算法[9],它将RRT向目标点的位置偏移,这样RRT算法就可以得到一个较优的规划路径。D.Ferguson和A.Stentz尝试着运行RRT算法数次来降低路径成本[10],多次运行后也能收敛到相对较优的路径,同时算法多次运行后得到的路径成本较小。S.Karaman和E.Frazzoli提出了RRT*算法[11],它改变了原始RRT算法中挑选父节点的操作过程,并使用成本函数挑选出扩展结点域中成本最低的一个点作为父节点。然后,每经过一次迭代后重新连接树上已经存在的节点,进而确保计算复杂度和渐进最优解。
然而,RRT*算法的缺点在于它的最优化是用降低收敛速度和增加搜索持续时间为代价的。文献[12]引入了目标偏置策略,它让随机生成树有目的地向目标点延伸,但是目标偏置策略会导致一些随机性缺失,削弱避障能力,并有可能导致陷入局部最小值,文献[13]提出了规避步长延伸法,它可以使随机树合理地远离障碍区域,避免陷入局部最小值。
以上方法虽然可以合理远离障碍区,可是在得到最优解上需要迭代次数过多,并且节点数过大,无法满足在低存储量的环境下的需要。因此,本文提出的Modified Informed-RRT*(MI-RRT*)算法在目标偏置策略的基础上,运用规避步长的延伸法,使快速扩展随机树在延伸时避开障碍物,并运用椭圆采样来减少得到最优解所需要的迭代次数,从而使得算法快速收敛,同时限制了最大节点数,降低了其所需的内存大小,能够运用更少的时间,快速收敛到一条相对成本较低的路径。然后经过相关实验证明了所提出算法的合理和可行性。
1 RRT*算法
由于RRT算法收敛速度慢等不足,Karamans跟Frazzolie改善了RRT算法的节点相连的操作,并发表出RRT*算法。与原始RRT算法区别在于,RRT*算法改变了父节点选择的操作过程,新增节点的同时检测采样点附近的节点,并在添加新节点后确定是否有成本更低的路径,如果有,则用新节点替换旧节点来对路径进行修正。
如图1所示,RRT*算法分为两个阶段:
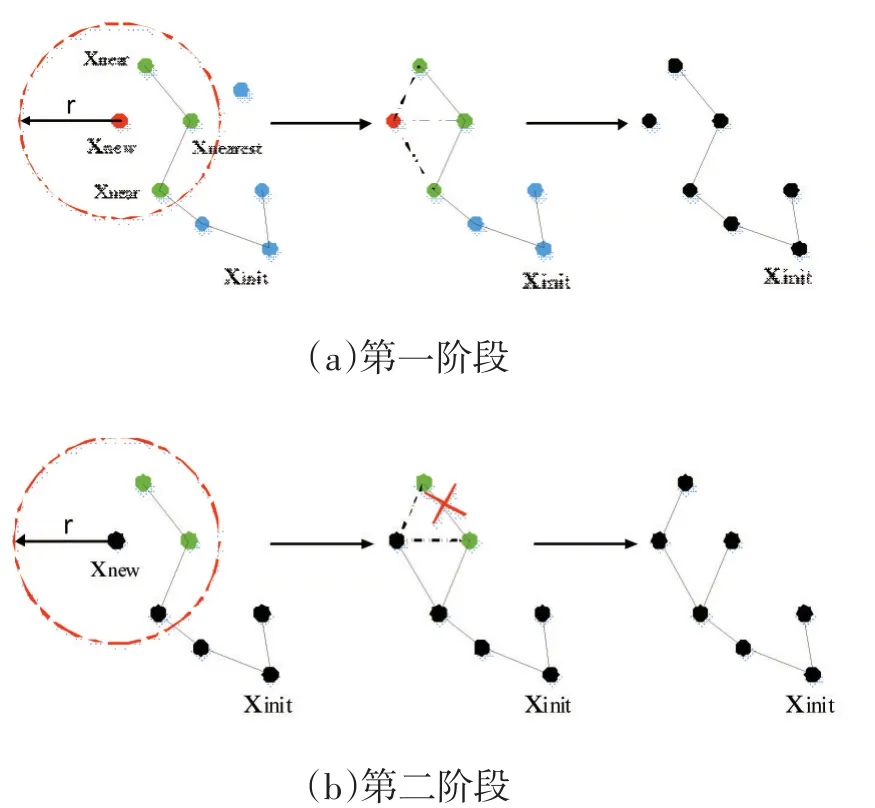
图1 RRT*扩展算法原理图
第一阶段:用最优解把xnew连到树上。
选择xnew的办法与RRT是一样的,接着以xnew为圆心,以r为半径画圆。获得的所画圆内的全部点,全部放入集合Znear。然后,迭代计算全部xnew→xnear+xnear→xstart的成本,选最小的那个与xnew链接。到此第一阶段结束。
第二阶段:验证经过xnew到达xnear另外的点的成本有没有比以前更小,若有的话,则连接新线。如图xnew向另外两个xnear连虚线。从经过xnew到达xnear,要是比从xstart到xnear的所用代价更低,就应用新边连接,移除旧边。
RRT*算法的主要步骤如算法1所示。
算法 1 RRT*(xstart,xgoal)
1:V←xstart;E←Φ;T←(V,E);i←0
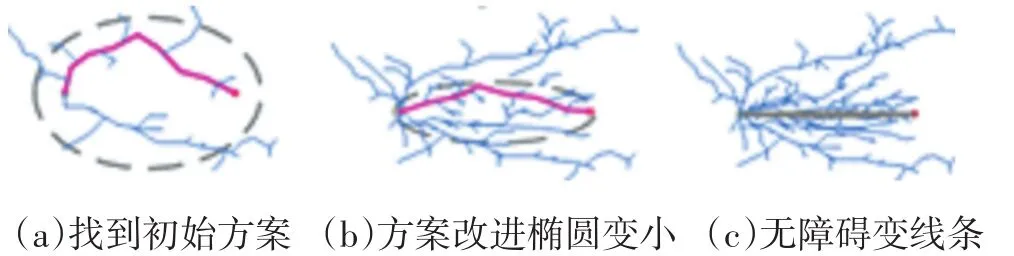
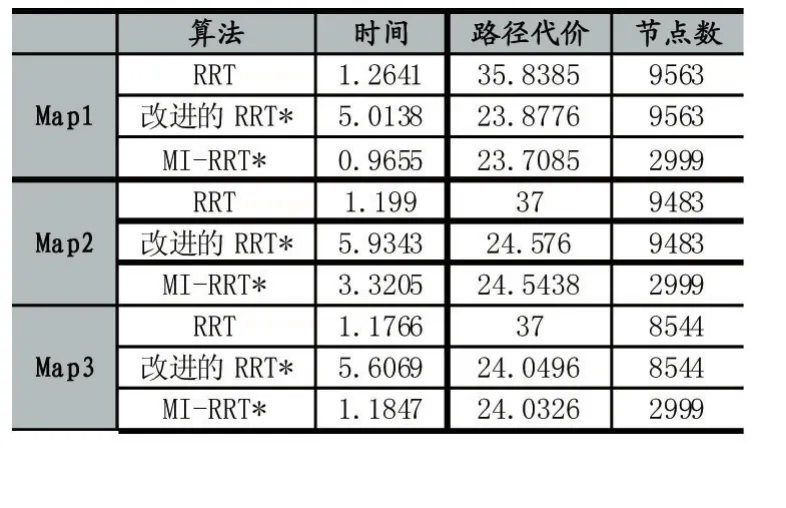
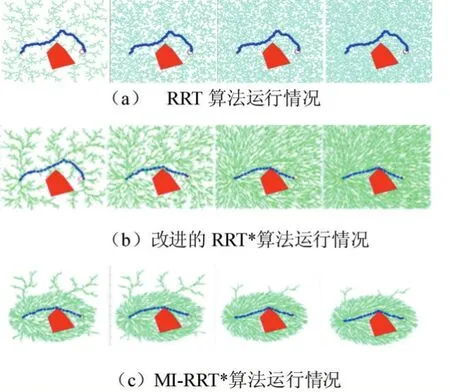
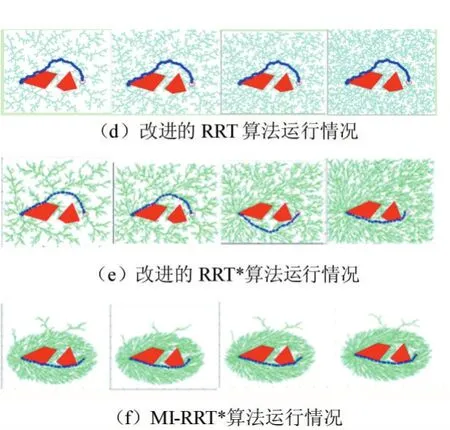
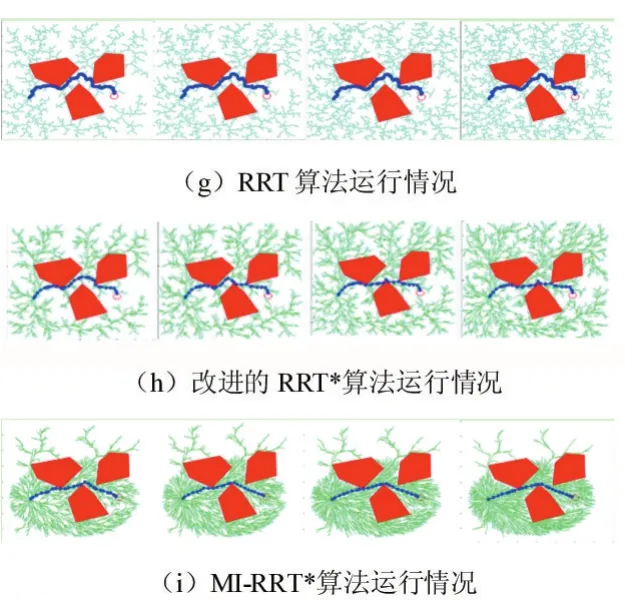
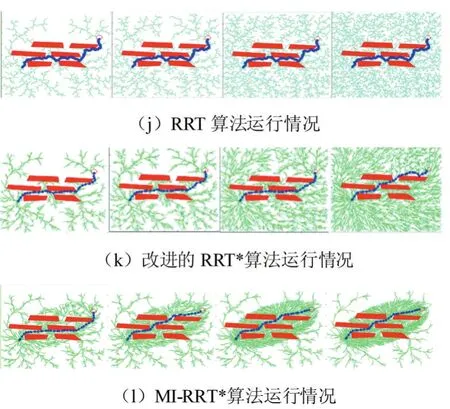
2:while i 3:xrand←Sample(i) 4:xnearest←NearestNode(xrand,T) 5:xnew←Steer(xnearest,xrand) 6:if CollisionCheck(xnearest,xnew)then 7:T←InsertNode(xnew) 8:xnear←NearNodes(xnew,T) 9:xparent←ChooseBestParent(xnew,xnear,T) 10:OptimizeVertices(xparent,xnew,T) 11:end if 12:end while RRT*算法优化了RRT算法形成的路径,留住了RRT算法的概率完备性的特征,增大了收敛速率,即经过较少的迭代生成代价较少的路径。 但是,RRT*算法需要在全地图中来搜索和采样,当区域环境中存有许多障碍之时,不小心就会陷入部分最小值,然后造成路径规划成功率变低。产生了大量结点,而且计算量随样本数量的增加而增加,在具有有限存储器的嵌入式系统中会产生阻碍,最后优化整个采样区域中的路径是困难的。针对RRT*算法的这些问题,提出了一种改进的RRT*算法,通过目标偏置,自适应步长延伸,修改结点、椭圆采样等方法对RRT*算法进行改进。 下面分别对4个改进策略展开解释。 以文献[13]为参考,文章中先根据均匀概率分布获取到一个随机数p,当p小于预设的阈值pmax时,则选择目标点xgoal为采样点,否则,根据原始方法在全局区域中随机获取采样点。文献[13]显著减少了RRT*算法的随机性,不必在全地图中来搜索和采样,加速了RRT*向目标点的扩展。 然而,要是p值过大,扩展树延伸到最终目标点的趋势很强,但是随机树生长的随机性受到限制,并且难以绕开障碍区域,导致路径规划的失败;要是p值过小,随机树具有很强的随机性,经过多次增长后,它才可以达到最终目标点并获得可行路径。然而,所获得的路径将存在绕远行为,这降低了移动机器人实际操作的效率。为了尽可能缩短路径,采用了一种不一样采样规则,一次选取2个临时目标点,其中临时目标点xrand1为最初的目标点,另一个临时目标点xrand2为空白区域随机选取。根据采样点xrand2选择最近的节点作为xnear。 影响RRT*算法规划速度的主要环节是选择xnear的过程,因为该过程需要遍历当前随机树的所有节点并依次计算与xrand的距离。临时目标点采样规则与步长调整规则相结合,以尽可能朝向目标点延伸。当扩展新的节点时,在节点xnear处优先朝向目标点xrand1延伸步长ε,并且当难以延伸时,将步长调整为0.5ε再次尝试扩展新节点。如果扩展再次失败,它将向临时目标点xrand2扩展,此过程无需重新选取xnear。 在原始RRT*中,如果设置的步长很小,则随机树的增长速度将过慢,这将影响得到解决方案的速度;如果设置的步长较大,在障碍较多的环境下,新节点将难以在该环境下延伸,同时降低了得到解决方案的效率。为了解决这个缺陷,本文引入了一种动态步长的策略。如图2所示,Di为距离xrand最近的障碍边缘的距离,εmin,εmax为设定好的最小,最大步长。 图2动态步长延伸策略 根据式1计算出步长: 用这个公式计算出的步长保持在最小和最大步长之间。在靠近障碍物的情况下,传统固定步长生长方法可能会无法通过障碍检测,这将会降低路径规划效率,而本文提出的动态步长则可以在障碍物附近生成有效的采样点。 在远离障碍物的情况下,传统固定步长生长受限于固定步长,导致随机树在空旷区域生长缓慢,而本文的动态步长可以按照最大步长来生长,增快RRT*的生长速度,随之减少了找到初始解决方案的时间。 随着解决方案的优化,树中的节点数量会无限增长。要是我们在具有存储量有限的嵌入式系统内实现RRT*算法时,将会出现问题。 针对节点数量无限增长的问题,我们引入了去除满足一定条件的节点来限制最大节点数[14]。在达到固定数量的节点后,它继续对树进行优化。具体地说,改进的RRT*使用RRT*的骨架,并用节点移除过程来丰富它。最初,树生长与RRT*相同,直到达到最大数量的节点M。如果此时没有一条到达目标点的可行解决方案,则必须重新启动算法。然后,每当添加新的节点时,改进的RRT*就删除一个节点。 图3节点插入、重新布线和删除 图3通过简单的2D图描述了改进的RRT*中添加新节点的过程。当且仅当从初始状态到当前状态的成本降低并且树中至少有一个没有子节点或仅有一个子节点的节点,才添加新节点。要添加新节点,将从树中删除一个不拥有子节点或仅有一个子节点的节点。要是有几个没有子节点的结点,则任意选择当中的一个结点。因为要是节点没有子节点,也就表示其不在通往目标状态的路径上。 第一次执行结点删除过程是在父节点优化期间。一旦xnear中的节点是xnear中另一个节点的唯一子节点,并且起始点经过xnew到这个子节点的累积路径成本低于原始路径,则子节点将重新连接,作为xnew的子节点并删掉父节点。我们观察到存在无法添加节点的情况,因为在xnear中没有要删除子节点的节点,它可能会降低RRT*的收敛速率。为了缓解这种情况,采用全局节点移除过程。节点移除在整个树中搜索没有子节点的结点,并随机删除一个结点。要是在节点优化和节点移除中不能找到要被删掉的节点,则在树中删掉xnew。 之前RRT*算法的采样是对全部状态空间来均匀采样,从而产生了大而密集的采样空间。然而,在得到初始路径再改善到成本最小路径时,树到各自树的根的所用成本大于现在找到成本最小路径的采样点,对最优解决方案的生成没有多少帮助。传统RRT*算法对上述采样点进行了许多的操作,上述采样点也使用了一部分的存储量,同时也影响了算法的效率。 针对RRT*算法的这个不足,文献[15]提出了一种算法,运用椭圆采样来降低无效采样点的数量。改进RRT*试图通过直接获取由n维椭球约束的起点和目标点之间的区域中的样本来最小化路径的成本。用这种方式,改进RRT*仅将解决方案的路径限制在椭圆体内,即启发式采样域,而不是整个自由空间,从而提高收敛速度并增加找到不易找到的路径的概率。它是RRT*算法的简单扩展,它不做任何额外的假设,并且与使用启发式偏见的其他算法不同,它不会扩展无法改进解决方案的节点。但其初始椭圆子集由RRT*全局搜索生成,整体时间花销大,结合本文目标偏置和动态步长延伸可以较好的解决初始路径花销大这个问题。 如图4所示,这是一个椭圆的采样视图,cmin是xgoal和xstart之间的真正距离。cmax是到现在为止找到的最佳路径的成本。当cmax接近真实距离时,椭球会缩小。找到目标后,所有样本都从这个椭圆形区域内取出。 图4椭圆采样视图 通过从一个单位n维球中第一次采样xball,从Xf均匀地采样点xf,然后计算以下过程: 其中C被定义为下面这个式子: U,是酉矩阵,可以通过奇异值分解(SVD)即U∑VT=M获得,M定义为: 这里l1T表示单位矩阵的第一列的和: 其中L定义为: L在这里表示xstart和xgoal之间的实际距离,通常由欧几里得距离决定。 xcentre是椭圆体的中心,用于平移椭圆体,定义如下: 与原始RRT*的不同之处在于,在找到路径之后,算法通过只聚焦于开始和目标中的范围来减少搜索空间,同时逐渐缩小椭圆体以找到最低成本的路径。由于其集中搜索,该算法对规划问题的维度和领域的依赖性较小,并且能够更快地找到更好的拓扑不同路径。它还能够在比RRT*更严格的公差范围内找到解决方案,并且计算量相等,并且在没有障碍物的情况下,可以在有限时间内找到机器零点内的最优解决方案。 图5无障碍物时椭圆采样 如图5所示,起始状态和目标状态分别显示为绿色和红色,相隔100个单位。当前解决方案以红色突出显示,椭圆形采样域显示为灰色虚线用于说明。随着解决方案的改进,采样域逐渐变小,从而可以产生最优解的效果。图(a)显示了第59回迭代完第一个解,(b)第175回迭代完和(c)第1142回迭代完的最终解,此时椭圆已变化为为起点和目标之间的线。 为了证明所提算法的可行性,将该算法在具有障碍的二维简单环境中运行了实验来证明,再比较了RRT,改进的RRT*[13],以及MI-RRT*算法的规划结果,仿真所用硬件环境为Win7系统,Intel Core i5-7500CPU@3.40GHz,8GB 内存。 在二维简单障碍环境下,RRT算法,改进的RRT*算法和MI-RRT*算法在不同的Map下的实验。如图所示,其中图6-图8为RRT算法、改进的RRT*算法和MI-RRT*算法的运行情况,算法的迭代次数从左到右依次增加。图中的方块是障碍物,左侧是起点,右侧圆圈是终点,曲线为最终路径。RRT,改进RRT*和MIRRT*的半径r都设为1.5,改进的RRT*最大节点设置为N=3000。实验进行10次,计算其平均值。 通过对三种算法运行情况的比较,本文的所提算法有更高的收敛速率,而且得到的解决方案更优,在经过多次迭代后,MI-RRT*算法生成的分支和路径比改进的RRT*算法更优。并且能够看出,在引入限制节点数量后,MI-RRT*算法生成的路径耗费的节点有了限制。同时,能够清楚地看到,该算法不但在运用椭圆采样后,采样点大量变少,并且也将采样点收敛到成本最小路径。 表1列出的是在Map1-Map3路径规划成功之后获得的数据,表中的数字是算法在每个Map运行10次取平均值。在Map1中,MI-RRT*在相近路径代价情况下,用更少节点节省了80.7%的时间,在Map2中,节省了44.0%的时间,在Map3中,节省了78.9%的时间。通过实验数据可以观测出,RRT*相比RRT可以在搜到更优路径,MI-RRT*相比改进的RRT*在更少的节点数的情况下能用更少时间的搜索到更优的路径。 表1对比算法结果表 为了使对比效果更明显,实验选择了一些障碍,使得起点和终点之间的真正最短路径存在狭窄的间隙。演示了算法的性能,观察了算法的收敛性,并对算法分别进行了2200、3000、5000和7000次迭代。最好的路径是通过中间的狭窄间隙。图中9-11算法的迭代次数从左到右依次增加,可以看到,改进的RRT*在7000次迭代时找到了一条穿过窄间隙的路径,而MI-RRT*在3000次迭代的时候找到了一条穿过窄间隙的更好路径,并且耗费的结点更少。RRT从不通过中间的窄间隙向目标发送路径。 图6 Map1下三种算法对比 图7 Map2下三种算法对比 图8 Map3下三种算法对比 图9 本文提出了基于改进的RRT*移动机器人路径规划算法,而且运用仿真实验验证了其可行性与优势,得到以下结论: (1)改进RRT*算法,初始路径生成时,采用目标偏置和动态步长延伸,使得到初始解决方案的速率和质量得到提升。 (2)采用椭圆采样,增进了本文提出的MI-RRT*算法的收敛速率。 (3)进行结点控制,减少了生成树所占用的存储量大小。2 改进RRT*算法的改进策略
2.1 目标偏置模型
2.2 动态步长


2.3 限制RRT★节点数量
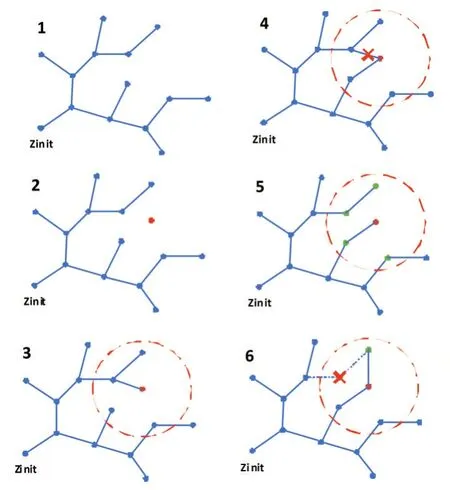
2.4 椭圆采样
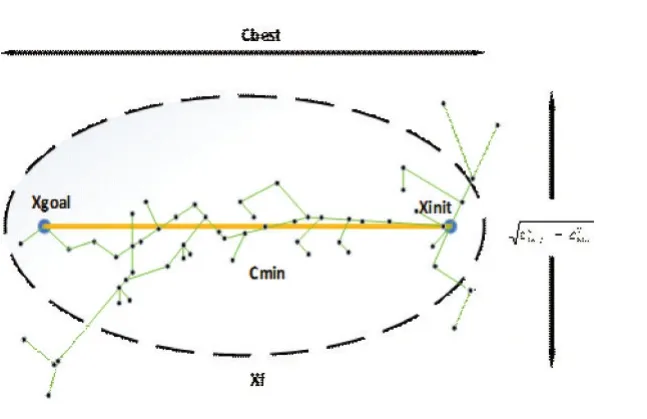

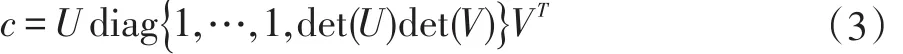
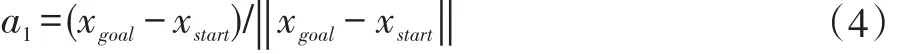

3 实验仿真与结果分析
4 结语
