面向学困生的高等数学教学实践与探讨

2020-04-07张京良

高教学刊 2020年9期

张京良

摘要：学困生管理问题是高校学生工作中的难点问题，高等数学学困生在高校学困生中所占比重较大，探讨面向学困生的高等数学教学方法是高校教学质量与学生未来发展的现实需求。调查与分析了高等数学学困生考试不及格原因，以建构主义学习理论为指导，在高等数学重修班教学中采用了混合式教学方法，探讨了开展混合式教学的一些措施。教学实践表明，混合式教学方法对促进高等数学学困生的学习主动性具有明显效果。

关键词：学困生;高等数学;课程重修;混合式教学

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2020）09-0113-04

Abstract： Management of students with learning difficulties is a difficult problem facing to college students. Among all students with learning difficulties， those in advanced mathematics have a large proportion. So exploring the teaching method of advanced mathematics facing to students with learning difficulties is real demand concerning teaching quality of a university and future development of a student. By investigation and analysis to the reasons why the students with learning difficulties failed to an exam in advanced mathematics， and guided by constructivism learning theory， it is suggested that blended teaching should be used in the class composed of students retaking advanced mathematics. Also， some measures on blended teaching are introduced. Teaching practice shows that blended teaching can promote effectively the activity of learning advanced mathematics to students with learning difficulties.

Keywords： students with learning difficulties; Advanced Mathematics; retaking a course; blended teaching

一、概述

学习困难，也称学习失能或学习不良，这一概念最早是由美国学者Kirk（1962）提出的[1]。我国各个高校中每年都有一部分学习困难生（简称学困生）因学业成绩不良拿不到学位证、毕业证，有的甚至留级、退学。根据教育部数据， 2012年全国高校本专科招生人数是688.83万[2]，到了2016年毕业人数却是704.18万[3]，相差15.35萬，说明前几年不能正常毕业人数超过十多万，而且这一数字呈现出逐年递增的趋势[4]。所以说，大学生中的学困生已成为一个不容忽视的特殊群体，学困生的学习问题不但直接妨碍了学生自身的未来就业与发展，而且也影响了高校的教育质量与声誉，学困生问题已经日益成为高校学生工作中的重点和难点[5]。

在大学学困生中，相当一部分是高等数学学困生。以我校为例，近几年高等数学考试不及格学生约占考生总数的15%左右，有的班级比例更高，甚至超过20%。另一方面，高等数学的学习在学困生的学业中又占有相当重要的地位。它不但能为学生学习专业课程提供必要的数学基础知识，而且还能训练学生的分析问题、解决问题、逻辑表达、抽象思维等多项能力，进而提高学生的数学素养。所以各级各类大学都把高等数学作为一门公共基础课，不但理工科院系要求学生必修此课，甚至一些文科院系也要求学生选修此课[6]。因此，探讨学困生的高等数学学习问题具有重要的现实意义。

包含我校在内的众多高校实行学分制，以前对这些学习困难生没有针对性政策，仅是允许他们重修，让他们插入到新生教学班跟新生一起学习。教学实践发现：这些重修学生要么觉着已经学过一遍了，对再听一遍没有兴趣，要么上课时间与自己所选本年级的其它课程冲突，经常不按时上课，缺课、逃课现象严重，最后学习效果也不佳。考虑到这些实际情况，我校近几年探索开设了面向学困生的高等数学重修班。鉴于重修班与普通班的授课对象不同，探讨重修班的教学模式是很有必要的。

二、高等数学学困生考试不及格原因的调查与分析

为了准确掌握高等数学学困生考试不及格原因，制定相应教学策略，我们对我校165名高等数学学困生进行了问卷调查。分析发现，高等数学学习效果差的原因主要体现在以下几个方面。

（一）客观综合原因

1. 学习氛围影响

当前社会网络信息发达，学生极易受到各种不良社会风气的影响，比如“一切向钱看”、“读书无用论”等。这种功利性极浓、浮躁性极强的社会风气已经蔓延到了学校的学习氛围中[7]，当然也影响到了直接实用性弱、理论抽象性强的高等数学的学习。

2.数学基础、生源背景的影响

我校实行“有限条件的自主选课制”，在同一类高等数学授课中，不同专业的学生可以根据自己的实际情况选择授课班级。这就出现了在同一班级中，学生的数学基础差异较大—有的较强，有的薄弱;生源背景不同—有文科生，也有理科生。在我们进行的学困生调查中，高考数学成绩低于90的占3%，介于90与110之间的占24%，介于110与130之间的占51%，130分以上的占22%;文科生占16%，理科生占84%。教师授课时没有兼顾到学生的差异性也是影响高等数学教学效果的一个因素。

3. 高等数学本身的原因

一方面，教学内容多、教学课时紧。高等数学内容包含了17世纪到19世纪末的微积分的主要成就，这一时期微积分研究活跃、成果众多，但学习期限却只有一个学年（180学时左右）。另一方面，高等数学内容抽象性强、理解起来难—微积分内容属于变量数学时期内容，这一时期对数学定义、定理的描述多以符号表示，以达到简洁、严格之目的。这些都影响到了学生的学习。

（二）学生自身原因

1. 学习态度消极、学习兴趣不浓

调查中，选择不喜欢数学的占49%，选择无所谓的占24%，选择喜欢数学的仅占27%;65%的学生学习高等数学仅仅是因为高等数学是公共基础必修课，不学不行。

2. 学习思想松懈、学习投入不够

许多学生在经历过高中高强度和高压力的学习后，认为进入大学后可以好好放松一下，学习思想松懈、学习投入较少。调查中，每天用在学习的时间在一小时之内的占49%，介于二小时与三小时之间的占46%;占用课外时间最多的活动中，选择上网的占68%，选择社团活动的占22%，选择其它的占10%;每天上网的时间在二小时与三小时之间的占58%，超过4小时的占31%。可见，这些学困生把大量时间都用于了上网。

3. 学习习惯不良、学习策略不对

作为“学习困难”高发群体，大一新生身上的学习策略失调显得比较突出，原因在于从中学转向大学，对大学学习缺乏足够的准备，学习方法和学习习惯未能及时转变过来。在我们的调查中，在课前预习、课后复习的选择中，选择从来不会的占13.4%，选择很少会的占67.1%，选择经常会的仅占19.5%;课堂上认真听讲的仅占8.4%，大部分时间认真听讲的占49.1%，偶尔认真听讲的占36.4%，基本不听的占6.1%。在学习策略方面，有研究表明[8]，43.1%的大学生常感到不知如何巧妙地记忆，对于十分抽象的知識，有38.5%的人常感到不知道如何去学习才好，认为教师所授知识太多太杂，不知如何归纳的有35.4%。

（三）教师授课原因

1. 教师教学方法单一

在我校高等数学教学中大多数教师仍然使用板书与讲解为主的传统授课法，教学方法单一、教学手段单薄，没有根据授课内容的不同选取相应的教学方法，也没有采取有效措施调动学生的学习积极性，自始至终满堂灌，造成了学生的学习兴趣低下。

2. 教师教学投入不够

高校教师，特别是年轻教师科研压力大，对教学投入不够，仅把课程教学当成一项任务来完成，缺乏教学热情，造成教师枯燥地教、学生枯燥地学的不良局面。

3. 教师教育理论缺乏

高等数学教师具有扎实深厚的数学专业知识和数学素养，但大多没有系统学习过教育教学理论，教学中所用的教学理念和教学方法多是通过回顾自己受教育经历和模仿有经验教师获得的。对高等数学教师进行教育教学培训，使其了解教育教学理论，特别是数学教学理论、教学方法是很有必要的。

三、高等数学学困生教学方法的选择

（一）以建构主义教学理论为指导

通过上面对高等数学学困生考试不及格原因的分析，发现在学困生的高等数学学习过程中，存在两方面的主要原因：一是学生方面，这些学困生学习不积极、不主动;二是教师方面，主要在于教学方法不当，仍以知识灌输式的传统教学为主。如果要改变学困生的学习局面，这两方面必须改进。与我们需求符合度最高的现有教学理论中，我们认为当属建构主义理论。

建构主义理论[9]是认知心理学派中的一个分支。这种学习理论认为：学习是引导学生从原有经验出发，生长（建构）起新的经验——学习不是由教师把知识简单地传递给学生，而是由学生自己建构知识的过程;学生不是简单被动地接收信息，而是主动地建构知识的意义;教师是学生建构知识的积极帮助者和引导者，学生是教学活动的积极参与者和知识的积极建构者。建构主义的核心可以概括为：以学生为中心，强调学生对知识的主动探索、主动发现和对所学知识意义的主动建构;而不是像传统教学那样，只是把知识从教师头脑中传送到学生的笔记本上。

自20世纪中期开始，美国教育以建构主义理论为指导，积极倡导“以学生为中心”的本科教育理念，致力于推动学生从被动学习转变为主动学习，引发了本科教育观念、教学方法和教学管理的系列变革[10]。在我国，2010年颁布的《国家中长期教育改革和发展规划纲要（2010-2020年）》也指出[11]：把育人为本作为教育工作的根本要求;要以学生为主体，以教师为主导，充分发挥学生的主动性。本质上也体现了“以学生为中心”的教育理念。

可见，在以学困生为对象的高等数学重修班教学中确立以建构主义理论为指导，践行“以学生为中心”的教学理念是与教育要求相适应、与现实需要相符合的。

（二）选定合适的教学方法

近几年，为实现“以学生为中心”的教育理念，许多以培养学生主动学习能力、提高学生学习效果为目标的教学方法被应用到教学实践中，如案例教学法、项目式教学法、问题驱动式教学法、团队合作学习法、同伴教学法、及时反馈法、翻转课堂教学法、混合式教学法等等，这些方法中有一些也被应用到高等数学的课堂教学中。

这些方法中，我们认为很多并不适合应用于高等数学重修班的整个教学活动中：案例教学法与问题驱动教学法对某些有应用背景的数学知识的讲授是合适的，但对理论性强的部分就不太合适;项目教学法在工程类课程比较合适，数学类课程中一般较少使用;团队合作教学法对专业相同、相互熟悉的学生较为合适，对来自不同专业、互不相识的选课制下的学生不太合适，因为团队难以稳定，联系不便，合作较为困难;同伴教学法对概念類知识的理解是可以的，应用到花费时间较多的数学计算部分就不太合适了;及时反馈法对小班授课比较实用，而我们的重修班学生较多;翻转课堂对一些文科类科目较为合适，由于数学的抽象与高难度，纯粹的翻转应用于数学教学也不合适。

比较后我们认为：混合式教学模式[12]更适合于高等数学重修班的教学。混合式教学体现在线上与线下学习相结合，这与我们的要求相符合：首先，学生已经学过一遍或几遍高等数学了，虽然考试没有及格，但还是具有一定的高等数学基础，具备了利用线上资源进行预习、复习的条件;其次，在学生具有一定基础知识的前提下，课上（线下）教师可以对部分内容略讲或不讲，从而有更多时间用于提高学生的学习参与性，提高他们的学习主动性。

四、面向学困生的高等数学重修班混合式教学实践

在教学实践中，我们发现学生通过MOOC视频主动进行学习的效果难以达到预期—有的学生根本不看，有的看完后抓不住知识重点。另一方面，对视频学习效果的考核较难操作——如果以登录与观看次数进行，体现不出学习效果;如果以MOOC中原有测试成绩为准，发现学校不同，教材不同，授课内容有差异，特别是MOOC最后出成绩时间有时晚于我们期末核算成绩时间，操作起来多有不便。为此我们对一般意义上的混合式教学进行了改进，把MOOC视频当做学生预习与复习以及学习一般性知识的辅助手段，授课内容中的重点内容仍然放到课堂上进行精讲。概括起来，我们的教学模式是：精讲为主、视频为辅、多加练习、重视过程。

（一）用过程性评价引导学生学习

课程的综合成绩由期末考试成绩与平时成绩构成，各占50%。期末考试与普通班一起进行，试卷一样;平时成绩由以下几部分构成：上我院机房利用数苑网考试系统进行中间考3次，每次占10分，目的是督促学生学在平时，即学即会，而非直到期末考试前才学; 利用数苑网在线作业系统布置在线作业共9次，占9分，题目以客观题为主，锻炼学生对基本知识的学习与掌握;纸质作业不少于12次，占6分，以计算题为主，锻炼学生对综合知识的掌握与运用;平时表现5分，鼓励学生上黑板做题、知识讲解等，目的是提高学生的学习参与性，进而提高学习主动性。过程性评价的目的是培养学生重在平时的学习习惯，逐步提高学生的学习主动性。

（二）课前预习授课内容

我们选用爱课程网上西安交通大学的高等数学MOOC作为我们的线上学习资源。要求学生在课前利用教材以及该MOOC视频进行授课内容预习，主要掌握概念引入、性质描述、定理证明等一些基础性知识。

（三）课上精讲重点内容

1. 教学方法多元化

授课时，我们根据授课内容灵活选用教学方法，如启发式、反馈式、案例法、同伴法、小组互评式，或者选取部分内容请学生讲解的翻转式等等，不拘泥于传统讲授，以培养学生主动学习为目的。比如极限计算部分，采用了小组讨论式授课——请同学们总结概括极限的计算方法;方向导数部分，运用了问题驱动式教学——通过山坡陡峭度与铁板温度变化度两个实例引出问题并引领学生解决问题等等。

2. 讲清原理，基础为主

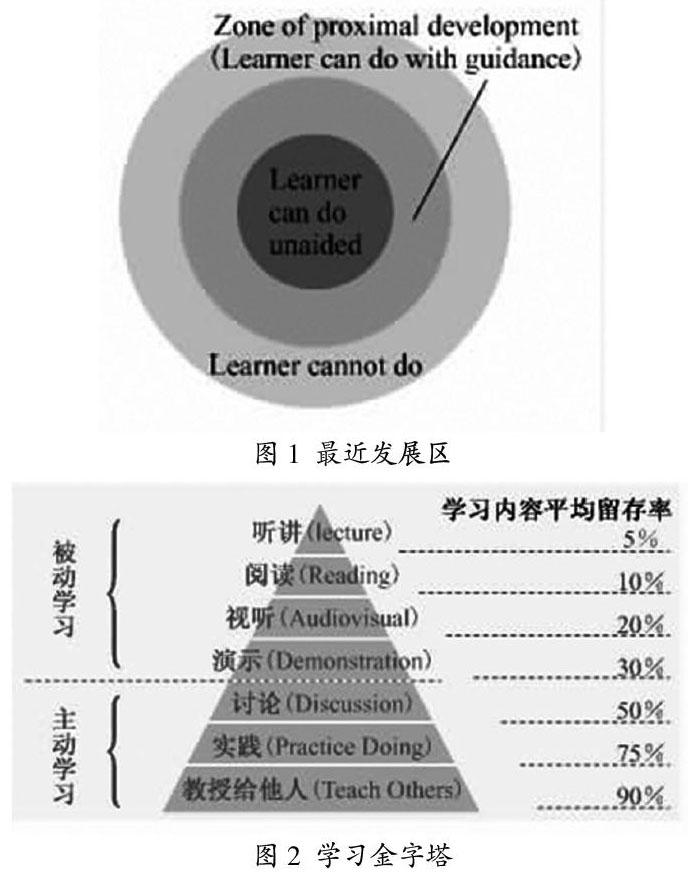
根据“最近发展区（Zone of Proximal Development）”理论[11]，学习者在接收新概念和新观点时，若这些新知识在其现有认知区域附近，则其学习效果最佳，这一区域即“最近发展区”（见图1）。若新知识难度过高，学习者能力不够，则会出现焦虑情绪;若新知识难度过低，学习者能力高，则学习者感觉无聊;若新知识难度过低且学习者能力也低，则会使学习者漠视新知识。对学困生而言，学习能力较低，为了使得他们接收的新知识在其最近发展区域内，授课内容不能过难，应该以基础性知识为主。

同时，根据建构主义认知论，知晓知识的前因后果能有效提高学习效率[13]。授课教师应当重视数学知识发生、发展、形成过程的教学，使学生知道所学知识的来龙去脉，讲清知识的原理，使学生知其然更知其所以然。

3. 精讲多练，以例服人

美国缅因州国家训练实验室基于研究，提出了一种现代学习方式的理论，用“学习金字塔”[11]（如图2）形象显示了采用不同学习方式的学习者两周后的平均学习内容留存率（average retention rates）。可见，实践训练是主动学习的一种重要方式，能有效提高学生的学习效果。

中国科学院院士刘应明教授也曾指出：“有效的解题训练，不仅可以使学生深入理解所学的知识，还能通过对各类问题的分析研究及寻求解法来培养学生的思维条理和创造力。”所谓的“听数学不如读数学，读数学不如做数学”就是这个道理。

正是由于课前学生利用教材与MOOC进行了预习，对授课内容中的部分知识有了了解，在课堂上对这部分知识就可以略讲或不讲，只对重要内容进行精讲，同时例题展示采用多媒体，这样与普通授课相比可以省出更多时间，将其用于课堂练习中，达到从“以理服人”到”以例服人”的效果。

4. 鼓励学生黑板做题、当众讲解

由图2可见，将知识教授给他人是最有效的一种主动学习方式。我们在实践中也进行了尝试，即为平时成绩中的5分课堂表现分。授课时，选取合适题目或合适知识点，鼓励学生上黑板解答并进行讲解，根据讲解质量进行评分。

5. 注重表扬学生

授课中可适当运用“罗森塔尔效应”[1]。美国著名心理学家罗森塔尔等人针对小学教育开展的一次心理期望实验后认为：教师通过行为表达让学生知觉并产生正向动力，有助于学生达到教师的心理期望。在“罗森塔尔效应”中，教师是权威者，教师恰当的评价和鼓励能够让学困生变得自信、自尊，并使学困生学会重新审视和正确评价自己，有助于激发出他们的主动学习性。

（四）课后巩固所学内容

为了巩固课上所学知识，课后我们要求学生做到：利用MOOC平台，对所学知识进行复习与释疑;完成在线作业，掌握基本知识;完成纸质作业，学会综合运用知识;使用微信群与公共信箱进行答疑交流、资料上传与下载等。

五、教学效果

（一）学生学习意愿有所增强

通过近几个学期的教学实践发现，采用这种改进的混合式教学方法，上课认真听讲的学生数、课下问问题的学生数、主动要求上黑板做题的学生数都有所增加，说明学生主动学习的意愿有所增强。

（二）学生学习能力有所提高

通过课堂提问，发现能用自己的语言描述定理内容的学生多了，说明学生对知识的理解能力有所提高;通过对当堂练习以及在线作业的正确率统计发现，做对的学生较多，这说明学生的运用知识的能力得到了提升;统计发现，主动观看视频、下载授课资料、完成补充练习的学生数增多，说明学生自主学习能力有所增强。

（三）学生对授课方式认可度高

调查问卷中，91%的学生赞同这种教学模式。

（四）学生综合成绩及格率有所提高

近几个学期，我校高等数学期末不及格学生直接参加补考后通过率在20%左右，而其他不及格学生参加重修班学习后，最后通过率都超过了60%，有时甚至超过了70%。

六、结束语

学困生的教学是大学教学面临的难点之一，应该根据各个学校的具体情况采取相应方法。我们对高等数学学困生的教学目前只进行了三个学期，经验仍然不足，还有许多方面有待探讨：比如在线资源辅助教学的完善问题，可以补充重、难点讲解微视频、习题解答微视频等;分析比较普通班与重修班的期末考试成绩;试行小班化重修班教学并与大班授课教学效果相比较等等。这些都是我们后期需要进一步开展的工作。

参考文献：

[1]张迎春，谈静艳.罗森塔尔效应在高校学困生转化中的应用[J].科教导刊，2012，11（上）：228-241.

[2]中华人民共和国教育部.2012年全国教育事业发展统计公报[M/OL][2013-08-16].http：//www.moe.edu.cn/srcsite/A03/s180/moe_633/201308/t20130816_155798.html.

[3]中华人民共和国教育部.2016年全国教育事业发展统计公报[M/OL][2017-07-10].http：//www.moe.edu.cn/jyb_sjzl/sjzl_fztjgb/201707/t20170710_309042.html.

[4]邱天龙，柴洁余，罗思亮，等.高校学困生与学优生课堂行为差异及转化策略[J].高教学刊，2016（23）：44-46.

[5]李玉环.高校学困生：现状、成因与对策[J].教学研究，2008，31（1）：41-44.

[6]尤慧，朱文芳.我国高等数学教学现状的研究述评[J].高等理科教育，2017（3）：91-95.

[7]段寧，赵晓朋.“高等数学”重修课程教学的探讨[J].科教文汇，2017，386（B）：55-56.

[8]张启钱，王小青，谈静艳.我国高校“学困生”的成因分析及对策研究——基于对“学习困难”定义回归解读的视角[J].高等理科教育，2011（2）：77-82.

[9]百度百科.建构主义[M/OL].https：//baike.baidu.com/item/%E5%BB%BA%E6%9E%84%E4%B8%BB%E4%B9%89/1428706？fr=aladdin.

[10]梁竹梅，谢艳梅，李鲍.以学生为中心的教学模式及其创新实践——上海交通大学首届教学学术会议综述[J].中国高等教育评估，2016（3）：75-80.

[11]范慧慧.以创新教学模式促进课堂中的“主动学习”[J].教学研究，2015，38（3）：8-27.