T型管道的冲蚀磨损数值模拟分析

彭方现 闫宏伟 李亚杰 袁飞

摘      要：三通管道作为石化行业中常见部件。针对天然气三通管道冲蚀破坏问题，采用标准k-epsilon模型，SMPLE算法，对T型三通管道内部流场进行了仿真分析。数值模拟结果表明：T型三通冲蚀部位最易发生在迎流壁面偏向出口处区域;流体速度和砂粒的质量流量对T型三通管道的冲蚀速率有促进作用;管道壁面的最大冲蚀速率在砂粒质量流量大于0.009 kg/s之后，增长幅度变大;最大冲蚀速率随着砂粒的圆球度数值的增大而减小，当颗粒中的圆球度在0.1至0.4之间变化时，最大冲蚀速率值减小的幅度相对较大，之后最大冲蚀速率呈缓慢减小的趋势。

关  键  词：T型三通管;冲蚀磨损;流体动力学;数值模拟

中图分类号：TQ 052      文献标识码： A       文章编号： 1671-0460（2020）03-0733-05

Numerical Simulation Analysis of Erosion Wear of T-junction

PENG Fang-xian， YAN Hong-wei， LI Ya-jie， YUAN Fei

（School of Mechanical Engineering， North University of China， Shanxi Taiyuan 030051， China）

Abstract：  The three-way pipeline is a common component in the petrochemical industry. Aiming at the erosion and damage problem of natural gas three-way pipelines， the internal flow field of the T-junction was simulated by the k-epsilon model and SMPLE solver. The numerical simulation results show that the erosion area of the T-shaped tee is most likely to occur in the area where the upstream wall is biased toward the exit; the fluid velocity and the mass flow of solid particles promote the erosion rate of the T-shaped tee; The maximum erosion rate of the pipe wall surface increases after the solid particle mass flow is greater than 0.009 kg/s; The maximum erosion rate decreases as the sphericity of the solid particles increases. When the sphericity in the particles changes between 0.1 and 0.4， the maximum erosion rate value decreases relatively， and then the maximum erosion rate decreases slowly.

Key words： T-junction; erosion; fluid dynamics; numerical simulation

因為管道运输具有结构简单、运输量大、高效节能等一系列的优点，所以管道运输作为目前最主要的流体介质运输方式被广泛使用，成为继公路、铁路、航空、水路等运输方式后的第五大运输方式^[1-4]。但是在管道使用过程中由于流体介质中不可避免地携带的一些微小颗粒物体，会随着流体介质的流动不断地冲刷管道内壁面，对管道内壁面造成冲蚀磨损的现象，造成管道壁面破裂发生泄漏事故，产生巨大的环境污染及经济损失^[5-7]。所谓冲蚀磨损，就是指小颗粒以一定的速度和角度对靶材表面进行撞击，使靶材的表面产生损耗。石油化工、航空航天、能源机械等领域广泛地存在冲蚀磨损现象，这也是设备失效的主要原因之一，对企业的安全生产造成重大影响，越来越引起国内外学者的普遍关注。

近年来，国内外一些有关专家学者采用科学实验或数值模拟分析的研究方法对不同类型下的油气管道的冲蚀问题进行了大量的深入研究。Vigolo， D^[8]等将实验结果与理论粒子追踪模型预测的轨迹进行比较，确定了黏性边界层在延迟粒子和降低与基板的碰撞速率方面的作用。随着计算机的发展，计算流体动力学软件也逐步应用于流体仿真计算中。Thiana A等^[9，10]在弯头外半径和几种不同的流动条件模拟了最大侵蚀速率、侵蚀位置。闫宏伟等^[11]研究了颗粒直径、入口速度及质量流量分别对弯头冲蚀速率的影响。许留云等^[12]得出了弯管的弯曲外侧70°～90°之间的位置为冲蚀磨损最严重的部位。

三通管件在化工行业中的应用也比较广泛，三通的主要功能是为了引导管内流体介质分流或者合流，改变了其内部流体介质的流动方向，三通部件通过使管道中的流体介质在分流或者合流过程中产生了较大扰动，进一步促使管内流动介质发生摩擦、碰撞，并加剧冲蚀现象的形成，因此受到冲蚀磨损的程度比直管严重50倍。其更容易发生泄漏危害。例如，我国迪那气田曾发生泄漏事故的原因，即为，三通发生穿孔而导致泄漏此外。陈宇等^[13，14]研究了异面三通管在不同工况下的冲蚀磨损规律。梁金川等^[15]分析了T型管道内部的流体介质的速度场和压力场。何兴建等^[16]分析了T型弯头的冲蚀情况，得出了在T型弯头盲管区域产生了漩涡，充当保护垫作用，能减缓壁面冲蚀。 除了三通管道本身结构、环境、材料因素的影响外，三通管道也会受到流体介质的速度、颗粒质量流量及颗粒形状等一系列的流体自身特征的影响。基于此，本文分析了流体入口速度、颗粒质量流量及颗粒的形状三种因素对管道冲蚀磨损的影响作用。

1  计算模型

1.1  湍流模型选择

根据流体动力学理论，流动状态划分的主要依据是雷诺数，当雷诺数超过2 300时，流动状态为湍流。其公式为：

             （1）

式中： —流体密度;

—流体速度;

—流动的特征长度，对于管道来说为管道直径;

—流體黏度。

经过计算管道内的雷诺数R_e>6 000，因此管内的流体运动状态为湍流。在流动状态中湍流是一种特别复杂的状态，无法全面准确地描述湍流状态。Fluent仿真模拟软件中有Laminar、k-epsilon和k-omega等模型。为了在保证计算精度的前提下，本文主要选用标准k-epsilon模型作为湍流的物理模型，因为Laminar模型是单方程模型，虽然其计算速度快，但不能保证其计算精度;k-omega模型的计算精度虽然和k-epsilon模型一样，但不易得到它的有关参数。k-epsilon湍流物理公式^[17，18]见式（2）、（3）。

   （2）

其中：                  （3）

式中： —湍流的动能;

 —沿坐标轴梯度方向湍流速度;

 —流体的密度;

μ_t —湍流的黏度;

G_k —湍动能数值的产生项;

 —湍流动能耗散的功率;

x_i和x_j  —空间中的坐标;

s_k —耗散能动函数对应的普朗特数，默认值为1;

s_e —湍流动能耗散的功率对应的普朗特数，默认值为1.2;

S_k和S_e —自定义值的参数;

在Fluent中，默认为C_μ=0.09、C_1e=1.44、C_2e =1.92。

1.2  冲蚀磨损模型

因为流体中固体小颗粒所占体积分数很小，所以选择DPM（Discrete Phase Model）模型来计算管道壁面的冲蚀磨损速率。在DPM模型中不考虑砂粒之间的相互影响，忽略砂粒本身的变化的影响^[19，20]，在该工程模型中，冲蚀磨损速率可用公式定义如下：

      （4）

式中：R_erosion —磨损碰撞速率，kg/（m²·s）;

N —颗粒碰撞时的颗粒入口数目;

m_n —碰撞颗粒入口质量流量，kg/s;

C（d_n）=1.8×10^-9 —碰撞颗粒直径系数;

a —颗粒入口折射角;

f（a）—碰撞颗粒的角度的计算函数，m/s;

v —顆粒的速度，m/s;

b（v） —颗粒速度函数;

u_n —撞击颗粒碰撞速度的计算函数，常数2.6;

A_face —碰撞壁面的计算单元面积，m²。

2  管道模型

2.1  管道模型及物性参数

T型三通管的几何模型如图1所示，其中D=50 mm;L₁=1 000 mm;L₂=500 mm。模型中连续相设置为天然气;离散相设置为砂粒，其密度为2 650 kg/m³。端口1、2为入口，两处天然气初始速度相同且在两管相贯处充分混合，经出口端流出。

2.2  网格划分和边界条件设置

利用Ansys meshing对T型管进行四面体网格划分，并在主管和支管相连接处进行局部网格加密，由于在管道近壁面处需要考虑流体层流影响，同时在管道壁面设置膨胀层网格。如图2所示。经过网格无关性检验，当网格数量数为393 801时最大冲蚀速率不再随着网格数量的增加而发生较大的变化。在入口边界条件设置中选择速度入口边界条件，操作压力选择默认值，连续相出口边界条件设置为选择outflow;离散相壁面边界条件设置为“reflect”，出口处设置为“escape”;选取SIMPLE算法，采用二阶迎风格式。

3  影响因素分析

在实际工程应用中，最大冲蚀率是考核管道安全的一个重要参数，T型三通管的冲蚀速率云图如图3所示，可知，在此流体流向的工况下T型管交汇处的迎流壁面处为T型管最容易发生冲蚀的部位，在迎流面偏向出口处区域为冲蚀速率最大的位置，而非入口1正对着的区域，因为由于入口2与入口1的流体在交汇处复合而使流体速度方向向出口方向处发生了偏移，故而使得冲蚀区域偏向出口区域，冲蚀速率也随着入口速度的增大而逐渐增大。因为入口1的速度和入口2的速度大小一致，所以模拟得到的冲蚀云图基本不变，即冲蚀易发生的具体位置保持不变。

3.1  流体速度大小与冲蚀速率的关系

管道内的流体的速度是影响冲蚀速率的重要因素之一。颗粒的质量流量设置为0.005 kg/s，颗粒的圆球度设置为1，其他参数不变，只改变天然气的速率大小进行数值模拟仿真，表1为不同的天然气入口速度下对应的最大冲蚀速率数值。

颗粒的质量流量设置为0.005 kg/s，颗粒的圆球度设置为1，其他参数不变，只改变天然气的速率大小进行数值模拟仿真，表1为不同的天然气入口速度下对应的最大冲蚀速率数值。

图4为最大冲蚀速率和天然气速度的关系曲线图，由其可知，最大冲蚀速率随着天然气入口速度的持续增大而不断增大，造成这样的主要原因之一是当管道内的流体速度较低时，由于固体小颗粒自身的速度较小，所对管道内壁的撞击冲量较小，故而冲蚀结果不明显;随着管道流体流动速度的不断增大，颗粒的动能由于气体的作用而增大，从而導致砂粒对管道管壁撞击时的冲量增大，对的管道冲蚀作用也就更加严重。

3.2  颗粒的质量流量与冲蚀速率的关系

颗粒质量流量体现了单位时间内撞击管道壁面的砂粒数量的多少。流体初始速度设置为2 m/s，圆球度设置为1，只改变颗粒的质量流量的大小进行数值模拟仿真。

表2为不同的质量流量对应的最大冲蚀速率值。

由图5可知，冲蚀速率和颗粒的质量流量呈正比例关系，即当颗粒的质量流量从0.001 kg/s增大到0.007 kg/s时，冲蚀速率呈线性增大;当质量流量从0.007 kg/s增大到0.009 kg/s时，最大冲蚀速率几乎不变，但当颗粒的质量流量大于0.009 kg/s时，最大冲蚀速率快速增大，呈指数式增长。造成该结果的原因是，随着质量流量的增大，单位时间内对壁面冲击的固体小颗粒的数量增多，对壁面的冲击力度增大，所以冲蚀速率增大。

3.3  颗粒的形状与冲蚀速率

颗粒的形状也是影响管道冲蚀速率的一个重要因素，当固体小颗粒的形状越不规则时，造成的冲蚀现象越严重。

体积相同的圆球的外表面积与颗粒的外表面积之比，称为该颗粒的圆球度。圆球度为无因次量，由于体积相同而形状不同的物体中，圆球的外表面积为最小，所以颗粒的圆球度恒小于1。圆球度的不同，说明颗粒形状与圆球的差异程度。当圆球度越接近0时，其形状越不规则，若其值越接近于1，则其形状也就越接近于圆球，当颗粒的形状系数为1时，其形状为标准的球形。

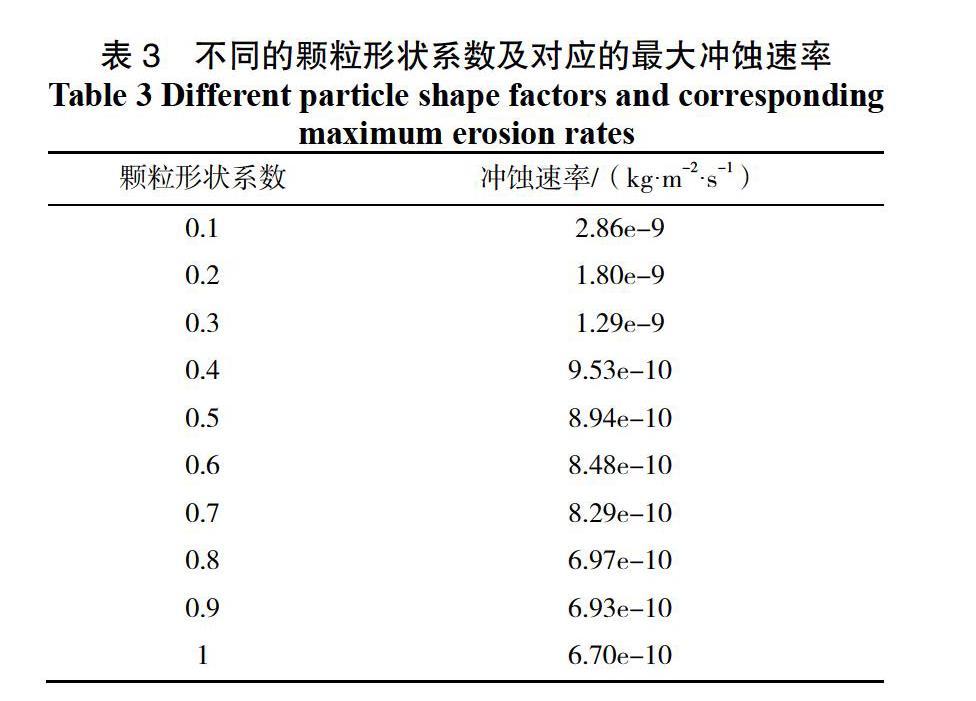
流体初始速度设置为2 m/s，颗粒的质量流量为0.005 kg/s，逐渐增大颗粒的圆球度的数值进行数值模拟仿真。表3为不同的颗粒的圆球度数值对应的冲蚀速率值。由颗粒圆球度数和冲蚀速率变化关系曲线图6所示，可知，颗粒圆球度在逐渐变大的过程中，管道壁面冲蚀速率却逐渐变小。

当颗粒圆球度由0.1增大到0.4时，冲蚀速率的数值由2.86×10^-9/（kg·m²·s^-1）减小到9.53×10^-10/（kg·m²·s^-1），减小幅度较大;当颗粒圆球度在0.4之后，随着颗粒的圆球度数值的增大，冲蚀速率呈缓慢减小的趋势。因为当砂粒圆球度数值由0到1变化时，颗粒形状逐渐接近于球状，对壁面的冲击的方式发生变化，由切削为主的磨损变为以研磨为主的磨损，造成的冲蚀破坏也相应地减小了。

4  结论

应用控制变量法针对T型三通管的冲蚀影响因素进行分析，得出了T型管道易磨损破坏的位置，可为石化管道的防护和检测定位泄漏提供合理的建议，通过设定不同的影响参数，得到的冲蚀规律为：

（1）在该工况下T型三通管的迎流壁面处最易发生冲蚀磨损，最大冲蚀速率发生在偏向出口的位置处，而不是正对迎流壁面处。

（2）冲蚀速率随流体速率增大而增大;

（3）蚀速率和砂粒的质量流量呈正比例关系，即当颗粒的质量流量从0.001 kg/s增大0.007 kg/s时，冲蚀速率呈线性增大;当质量流量从0.007 kg/s增大到0.009 kg/s时，冲蚀速率几乎不变， 但当颗粒的质量流量大于0.009 kg/s时，冲蚀速率快速增大，呈指数式增长;

（4）当砂粒圆球度系数由0.1增加到0.4时，冲蚀速率的数值减小幅度较大，呈指数式减小;当颗粒的圆球度为0.4之后时随着砂粒的圆球度的增大，冲蚀速率呈缓慢减小的趋势。

参考文献：

[1]谢文伟， 邓建新， 周后明， 等. 材料冲蚀磨损的数值模拟研究现状及展望[J]. 腐蚀与防护， 2012， 33 （07）： 601-604.

[2]涂亚东， 徐小兵， 殷华锋， 杜娇， 陈飞跃， 邱杰. 高压管汇冲蚀磨损规律研究[J]. 石油机械， 2018， 46 （02）： 84-88.

[3]许根富，王飞，赵哲明，等.石化压力管道冲蚀失效数值模拟及影响因素分析[J].中国安全生产科学技术，2016，12（04）：143-147.

[4]周三平. 基于斯托克斯数的弯管冲蚀数值模拟[J]. 腐蚀与防护， 2017， 38 （07）： 557-561

[5]孙海疆， 偶国富， 肖定浩， 等. 煤液化多相流输送弯管冲蚀磨损数值研究[J]. 流体机械， 2013， 41 （08）： 45-47+71.

[6]张孟昀， 马贵阳， 李存磊， 等. 弯管与盲通管冲蚀磨损对比分析研究[J]. 中国安全生产科学技术， 2017， 13 （03）： 76-81.

[7]孟康， 程永， 肖玲，等. 不同夹角T型三通流动特性的数值研究[J].黑龙江科技信息， 2010 （01）： 30- 31.

[8]Vigolo D， Griffiths IM， Radl S， et al. An experimental and theoretical investigation of particle-wall impacts in a T-junction[J]. Journal of fluid mechanics， 2013， 727： 236-255.

[9]Thiana A Sedrez， Siamack A Shirazi， Yeshwanth R， et al. Experiments and CFD simulations of erosion of a 90° elbow in liquid-dominated liquid-solid and dispersed-bubble-solid flows[J]. Wear， 2019， 426- 427.

[10]Yu Wang， Rongtang Liu， Ming Liu， et al. Numerical investigation onerosion characteristics of coplanar elbows connection for gas-solid flow[J]. Energy Procedia，2019，158.

[11]閆宏伟，崔子梓，焦彪彪，等.油气管道弯头冲蚀仿真研究及影响因素分析[J].热加工工艺，2018，47（06）：93-97+102.

[12]许留云，胡泷艺，姚赛，等.90°弯管内冲蚀磨损的试验研究和数值计算[J].当代化工，2017，46（02）：308-310+315.

[13]陈宇，马贵阳.异面三通管冲蚀磨损的数值模拟研究[J].润滑与密封，2018，43（03）：117-122.

[14]常乐，钱英豪，周鹏飞，等.埋地天然气管道三通的失效分析[J].压力容器，2011，28（09）：56-59.

[15]梁金川，邓又文，胡彪.模拟分析小颗粒对T型管的冲蚀[J].当代化工，2017，46（01）：145-148.

[16]何兴建，李翔，李军.T型弯头不同工况的冲蚀磨损数值模拟研究[J].化工设备与管道，2015，52（03）：69-72

[17]曹辉祥，陈小榆，徐婧源.气固两相流管道冲蚀规律研究[J].机械设计与制造工程，2018，47（08）：91-96.

[18]陈佳，刘勇峰.三通管冲刷腐蚀数值计算[J].当代化工， 2013， 42 （01）： 76-78.

[19]邹智鑫， 王合旭， 蒋彦龙， 李泽伟. T型三通管冷热流体掺混数值模拟[J].计算机辅助工程，2019， 28 （01）： 46-52.

[20]满文聪， 刘薇. 基于AnsysWorkbench的Y型三通局部应力分析[J].炼油与化工， 2015， 26 （01）： 23-25.