加强例题拓展 实现初中数学减负
2020-04-07林森海
摘 要:随着素质教育的逐渐深入,减负要求显得更加重要。减负不是减质量,而是通过精简课堂来增强效果。数学学科围绕简单的例题展开拓展,能够丰富教学内容、加强教学深度,在减轻学生负担的同时挖掘学生学习数学的潜力。本文基于数学教学现状,简要分析开展例题拓展的必要性,并以当前使用的初中数学教材为例阐述几种具体教学措施,以求为进一步促进初中数学减负增效提供思路。
关键词:例题拓展;初中数学;减负增效
传统教学模式下,教师主要靠督促学生多练题、课堂抓紧时间多讲题来提高学生的成绩。这样不仅于学生真正掌握数学真知、发展数学思维无益,而且会同时加大教师和学生的负担,因此,教师要主动改进教学形式,通过拓展例题讲解来提高教学效率,减轻师生负担。
一、 初中数学例题教学现状及拓展改进策略
许多教师奉行传统的数学教学方法贯彻题海战术,认为只要学生练的题型多、数量大、时间长,就能够形成数学思维、充分掌握数学解题的能力。其实不然,学生在面对众多的练习题时,一则会被反复出现的题型磨灭兴趣、消除动力,二则会逐渐迷失自我,无法区分不同题型、明确解题思路。因此,刷题看似是勤奋的体现,实际上却是事倍而功半,教师试图通过题海战术达到教学目标会导致增大学生压力、降低教学效率。数学教师培养学生数学思维、综合素养的有效手段是抓住课堂的宝贵时间,从例题入手优化讲解方式,通过围绕例题展开拓展延伸的方式传授多种数学方法与思维。
基于教学现状分析,教师可以改进例题讲解方法实现拓展训练的策略集中在以下三个方面:
一是有选择地讲解例题,在纵向上加强例题讲解的深度。现阶段教学中教师倾向于教材上的每道例题、辅导资料上的所有练习题都涉及,唯恐学生有弄不懂、学不会的地方,这样机械地训练效果不佳,教师应该避免盲目选题讲解的模式,挑选有代表性的典型例题来阐述,让学生循着教师的提示一步步独立思考,进而掌握数学原理、解题思路。
二是注重讲题方法,在横向上拓展例题讲解的内容。大多数数学教师的讲题方法还停留在就题讲题的层面上,习惯带领学生把标准答案捋一遍,这样学生只是单纯地听懂了却没有内化为自己的思维能力,因此教师要多加运用题型对比、题目转换等方法,来锻炼学生的数学思维。
三是联系实际、灵活探究,在多个角度拓宽例题覆盖的数学知识面。这是许多数学教师都会忽略的地方,教师为了确保学生能够集中精神于思考、解题上紧紧地围绕题目讲解,致使學生对数学的功能乃至数学这一学科缺乏了解。为了实现学生能够举一反三、学以致用这一目标,教师要摒弃过去生搬硬套、僵化单一的讲题模式,尽可能地发觉数学知识在生活中的应用,借助数学情境更加细致、全面地讲解例题。
二、 结合案例具体分析例题的拓展教学方法
(一)巧设问题串拓展,加强例题讲解深度
要想激发数学题的最大功效,教师讲题不能仅仅停留在表面,而要深度剖析题目,让学生对有限的题目不断挖掘,进而积累源源不断的新思维、新方法。为了促进学生主动探索,教师要改进过去照本宣科的解读方式,利用层层递进的问题激活学生的数学思维,从纵向层面拓展例题。为了实现这一目标,教师要选择内容丰富的例题,将要讲的知识概念悉数融合进去,同时尽量避免重复题型,让所有知识都能得到体现。
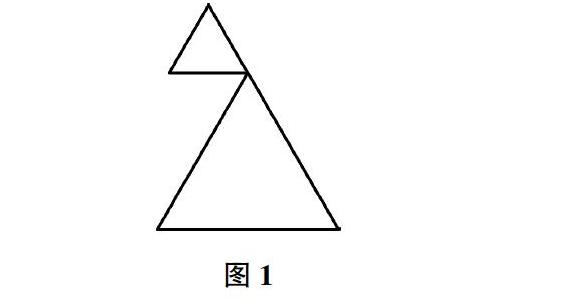
以七年级下册《轴对称现象》这节内容为例,许多教师在讲这节内容时,会让学生判断各种图形是否是轴对称图形,练习题中大部分也是这种类型。这样会让学生不由自主地采用惯性思维判断,而没有调动数学思维。为了培养学生对轴对称数学知识的掌握,教师可以选用这样一道例题:两个大小不一的三角形如图1所示排列,问这个组合图形是否是轴对称图形?怎样改变其中一个三角形能够将其变换为轴对称图形?在学生自己思考和动手绘图之后,教师可以让学生通过小组合作的形式交流,比一比谁画出的新图形具有的对称轴最多。通过这三个难度递进的问题,教师能够让学生由浅入深地感知轴对称的概念,将一道简单的例题丰富起来,而且借助合作学习的模式能够激发学生更多的可能,让学生围绕一道例题得到意想不到的收获。
设计问题串,在于“新”。教师针对一道题目设计多个问题,意在学生能够通过这些问题发现陌生的知识或方法。因此教师要避免流于形式的无效提问,基于学生的学习进度和客观事实精心考虑,提出最合理、最具探究性的问题。
(二)挑选多解题拓展,培养学生发散思维
许多数学教师在写教案准备例题时,教材上有什么就讲什么,将主要精力放在改进讲题过程上,而对题目不加以甄别,这样不利于发挥数学课堂的最大效用。数学题是做不完的,但课堂时间总有限制,因此教师要仔细研读教材,发觉最有解读价值的例题,利用数学课带领学生研究。数学中有一种特殊题型可以通过多种途径实现解决,叫做多解题。教师在带领学生剖析多解题的不同思路时,能够让学生站在多种角度思考,从而自发地积累解题方法、完善自身理论框架。教师借助一题多解不仅可以拓展例题,而且能够训练学生的发散思维,达到事半功倍的教学效果。
例如,教师在带领八年级学生学习《二元一次方程组》的知识时,可以设计这样一道例题:小茗买了13个苹果、5个桃子和9个西瓜,一共花了92.5元,小红买了2个苹果、4个桃子和3个西瓜,一共花费32.0元,那么小晴买1个苹果、1个桃子和1个西瓜需要花费多少钱?设苹果、桃子、西瓜三种水果的单价分别为x、y、z元,则根据题意有:13x+5y+9z=92.5①和2x+4y+3z=32.0②两个式子。后续的解方程组可采用多种方法,在此列举两种:一、 凑整数法,能够通过(①+②×4)/21直接得到(x+y+z)=10.5。二、 设主元法:将x和y通过z表达出来,即可得到x+y+z=5.5+5-z+z=10.5这一结果。教师通过展示不同的解题思路,能够催生学生的创新思维,拓展和加强例题的讲解效果。
除了解方程这一种类型,一题多解在平面几何题型上也有充分体现。数学教师在讲解平面几何题时,要抓住几何题无标准答案这一特点,鼓励学生产生丰富多样的解题思路。另外,教师还可以将“一题多解”与“一题多问”结合起来,更大程度、更高水平上拓展例题的讲解,让学生透过有限的题目积累知识、提高能力,从而减轻学生的练习、作业负担。
一题多解,在于“多”。这个“多”体现在解题思路、解题过程中,因此教师在讲解多解题时要重过程轻结果、重思维轻答案,将主要时间集中在引导学生想象与尝试上,在“殊途同归”中拓展例题。
(三)灵活变换题目拓展,引导学生对比总结
想必许多数学教师会有这种苦恼:考试题型和例题十分类似,已经讲了很多遍、很多道这种题了,但学生还是做不出来。这是因为学生缺乏知识迁移的能力,从根本上没认识到几道题能归为同种类型,自然只是教师讲一道会一道,变换形式就不会了。针对这种情形,教师要从培养学生的联想、对比的意识入手,可以在讲解例题的时候灵活地改变题目形式,进而让学生在对比中轻易地收获解一大类题的方法。
变换题目可以是改变题目的假设、条件让学生寻找新的答案,也可以是改变结论、图形引导学生发现对应的题目条件。例如,教师在开展八年级上册《一次函数》这节内容时,可以出这样一道题:已知函数y=(5+k)x+(7-x)是一次函数,求k的取值范围。然后改变题目结论,另y(x)函数为过(原点)的函数,求k的值。之后,教师可以让学生思考k为何值时,y随x增大而减小。这类题的变式有很多种,但都围绕着一次函数最基本的性质展开。因此教师可以通过改变细节来考查学生的掌握程度,同时让学生在相似的题目中对比总结出知识框架。
同时,教师可以鼓励学生扮演变换题目形式的角色,例如这道几何证明题:在等腰三角形ABC中,AD是∠BAC的角平分线,则有BD=CD这一结论。教师可以让学生思考,改变其中的某一条件得出相同的结论。这时学生能够联想到等腰三角形三线合一的性质,从而提出将AD变换为高线、中线、垂直平分線结论都不变的观点。通过这样能够有效调动起学生的课堂参与程度和思维积极性,有效利用起这道简单的平面几何例题。
变换题目,在于“比”。教师不仅要关注学生对一道题的掌握程度,更要引导学生观察题目的微小改变所引起的结果巨变,督促学生对比总结,构建一类题的解题思路。
(四)联系生活情境拓展,丰富课堂呈现形式
学生之所以畏惧数学、摸不清学习数学的门道,很大程度上是受数学知识过于抽象这一原因所累。例题对学生来说是陌生、崭新的,讲好例题是帮助学生理解一整部分数学概念的基础。为了增强课堂教学效果,教师首先要确保学生能够充分理解例题的题目、解题思路。为此,教师可以借助其他的方式,例如建立数学情境来直观地展现抽象难懂的数学概念,加上生动简洁的动画来描述解题思路。
以八年级下册《图形的旋转》这节内容为例,教师可以在课程导入时播放摩天轮、旋转木马等动画,让学生联想生活经验初步领会旋转的知识。之后教师可以给出一道例题,让学生画出△ABC分别顺时针和逆时针旋转60°、90°之后的图形。学生刚开始接触这部分知识时会容易迷茫,这时教师可以让学生用纸抠出一个三角形,然后用笔固定纸片的一端,将纸片自由转动来获得直观的印象。过程中教师可以引导学生回忆刚才观看的摩天轮和旋转木马的动画,找到固定点、旋转方向和角度。通过让学生动手操作和联系具体场景,能够更加形象地阐述道理,学生也能够更加深刻地记忆和运用。
联系生活,在于“活”。让生活情境成为承载数学知识的客体,教师要注重融合的方式,切勿强硬建立联系,而是采取合理、巧妙的方法,让学生不由自主地进入数学情境。
总之,例题是课程的基本要求也是核心内容,教师在讲解例题时多加拓展能够为学生提供更加全面的解题范例,同时促进学生发散思维、创新思维的生成。教师要选择优质经典题目,挖掘教材内容设计一题多问、一题多解、一题多变等丰富形式,再加上联系生活创设情境,实现例题拓展和教学减负增效。
参考文献:
[1]张东志.“减负增效”下初中数学智慧课堂的实践探析[J].数学学习与研究,2019(1).
[2]吴作明.优化例题设计 提升学习能力:基于“减负增效”下初中数学教学中的例题设计探析[J].基础教育论坛,2015(13).
[3]黄旭辉.“减负增效”教学策略在初中数学考试命题技术中的实践与研究[J].新课程(中学),2016(2).
[4]陆丽娟.拓展习题,开阔学生的思维:浅析应试教育背景下减负高效的题典策略[J].中学数学研究:华南师范大学版,2017(16).
作者简介:
林森海,福建省漳州市,福建省漳浦县东坂中学。
