井下掘进机行进纠偏调度规划与控制研究

2020-04-07瞿圆媛宋林珂吉晓冬吴淼

矿业科学学报 2020年2期

瞿圆媛，宋林珂，吉晓冬，吴淼

1.中国矿业大学(北京) 机电与信息工程学院，北京 100083

纵轴悬臂式掘进机(简称“掘进机”)是井下综掘工作面的核心设备之一，主要用于巷道成形。面对当前国内外煤炭领域无人采掘装备机器人化的发展趋势[1]，掘进机现场作业的少人化和智能化发展受到各生产研发、应用和研究单位的普遍重视[2]。机器人化掘进的实现需落实掘进机的位姿检测、自主纠偏、远程控制与自主截割等环节[3]。其中，基于位姿信息的行进纠偏(掘进机的行进调度)是保证巷道截割质量的重要前提。

掘进机采用履带式行走移动，与履带车在一定程度上较为相似。根据侧重点不同，地上的履带车辆轨迹规划与跟踪方案分为两类：一是在对履带车的动力学及运动学模型提出改进和完善的基础上，建立有效的控制模型。这类方案多侧重于分析动力学平衡，建立考虑履带与地面之间滑动摩擦力对运动参数影响的模型，如文献[4-5]讨论并运用了滑动操纵模型，文献[6-7]基于对履带车动力学模型分别针对小型履带移动机器人和深海履带车设计了路径跟踪控制策略，并不同程度验证和讨论了其控制效果。二是根据履带车动力学或运动学基本特征，着重开发更有效的跟踪控制策略或算法。这类方案是在模型预测控制(MPC)[8-9]应用于轮式机器人的闭环优化控制策略基础上进行改进，使模型更符合履带式车辆的实际行走特征，如文献[10]运用MPC模型结合陀螺仪的测量信息实现履带打滑率的自适应估计，由此完成移动机器人的轨迹跟踪控制。

上述研究为一般履带车的轨迹规划与跟踪的研究，但针对掘进机的轨迹规划与跟踪问题仅有少量文献涉及。如文献[11]将掘进机路径规划问题归类为一般性随机网络问题，提出最小耗费代价建模法以搜寻最佳路径目标点集；文献[12]对掘进机的液压行走驱动进行了建模，并针对行走轨迹偏离巷道中线的问题提出了模糊控制策略；文献[13]以掘进机液压控制系统为基础，提出了基于神经网络PID算法的自主纠偏策略。

笔者认为，掘进机的行进路径跟踪无论基于哪类控制模型都应根据对象的动力学与运动学特征，充分考虑控制量的实际意义与限制条件，合理引入实时可观测信息，以保证控制过程的可行性及可靠的跟踪控制效果。因此，围绕掘进机的行进纠偏调度的需求，根据掘进机行进特点及巷道成形要求制定机身纠偏调度规划，并基于掘进机行走机构的运动学特征建立位姿偏差模型，以机身行进位姿偏差收敛为目标建立跟踪控制模型，为掘进机井下偏航工况设计一套基本的控制策略和调度方案，为更复杂的无人化精准掘进研究提供必要的模型基础。

1 掘进机行走纠偏调度规划

巷道掘进时，要求掘进机按掘进巷道的中心线轨迹行进或调度。掘进施工程序为：根据掘进机当前位姿调整机身方向角，尽量保证机身的行进方向与待掘进巷道中心线相重合；按照巷道断面形状，利用截割机构截割煤岩并运用机身前后的铲板机构和输送机将落煤(岩)运送出去，截割过程中机身实现前移，完成1个掘进量；调整机身方向角和速度，进入下一个施工程序，循环行进。

每完成1个掘进量，机身搭载的定位系统[14-15]会测量当前的机身质点位置坐标，判断是否与设计的巷道中心线有所偏移，进而规划后继的掘进轨迹并调整工作参数。掘进机偏离中心线的表现有：① 方向角与掘进机当前位置中心线指向不一致；② 机身质点在中心线之外。鉴于掘进机自身外形尺寸较大，在纠偏过程中不可避免会开凿出衍生空间，即与理想巷道空间不符的部分。为使衍生空间尽量小，调度过程平滑，衍生空间应紧密依附于理想巷道主体周围。

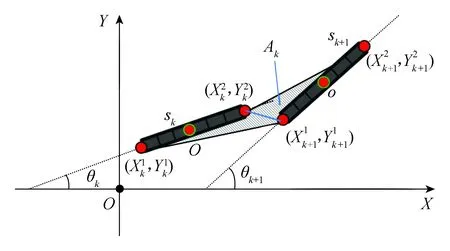
图1 掘进机机身纠偏调度示意Fig.1 The area swept by one side of the road-header during one movement

纠偏行进调度规划需考察由tk到tk+n时刻、机身由状态sk移动到状态sk+n所扫过的面积A，以及机身首、尾端点经过的极限位置坐标(Xk+m，Yk+m)。首先讨论机身以不同的行进速度v、角速度ω组合运动是否会得到不同的n、A与极限坐标位置。

图1中机身以一定牵引速度v、转向角速度ω移动1个掘进量前后的位置，由状态sk变为状态sk+1，图中阴影部分表征这一掘进过程中产生的衍生空间在地面的投影面积Ak。n个纠偏调度所产生的衍生空间投影面积为

(1)

(2)

忽略机身圆周运动的线速度，其质点的位移量主要取决于前进速度，即

(3)

由于θk+1=ω(tk+1-tk)+θk，式(3)可为

(4)

同理可得

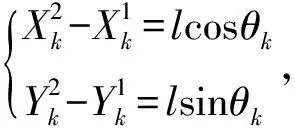
(5)

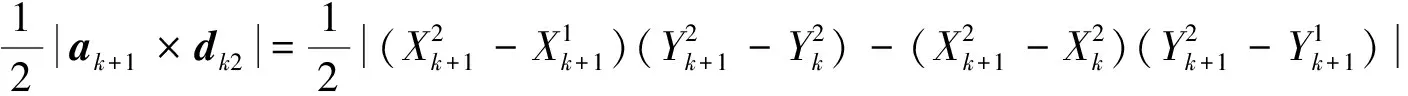
(6)

由式(2)、式(5)、式(6)可知，Ak与n、v、ω的取值有关，而n、v、ω的取值互相牵制，且需考虑实际工作参数和环境等因素的限制。行进调度实质上是针对机身与目标巷道的方向角、位置(X方向、Y方向)等偏差，给参数v、ω规划一组合理的取值(v0，ω0)，(v1，ω1)，…，(vn，ωn)，使掘进机逐渐回到目标巷道中心线上，具体取值由式(7)求解获得：

(7)

式中，Xd、X0分别为质点目标X坐标与初始X坐标；θd、θ0分别为机身的期望方向角和初始方向角。

式(7)表征在掘进机行进调度中，首先纠正机身上任一点在X方向的位置；其次要使机身方向角与规划中心线的切线方向一致；再次使产生的衍生空间尽量小。

除此之外，还可能针对下述情况提出明确要求：① 是否允许机身头部越过目标中心线；② 对调整周期n是否有限制；③ 在tk+n时刻机身某点的Y坐标是否有限制，即是否要求在限定的掘进距离和步数内完成调度；④ 机身行进速度与转角速度是否要求为恒定值，数值上有无限制，等等。

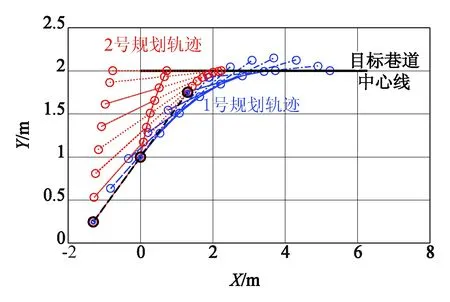
图2 掘进机调度轨迹示意Fig.2 Illustration of the possible trajectories corresponding to different considerations

1号与2号规划轨迹的对比见表1。

表1 1号与2号规划轨迹对比Tab.1 Comparison of the planned trajectories No.1 and No.2

2 掘进机行进调度位姿偏差模型

2.1 掘进机履带行进运动学模型

将掘进机简化为水平面上的刚性履带车，其转向运动一般并不剧烈。在机身上建立车载坐标系xoy，如图3所示。x轴沿机身中轴线指向前进方向；C表示机身转向的瞬心；XOY表示履带机器人所在的大地坐标系。机身直线运动时，履带侧向不受力；机身转弯时，履带与地面之间发生相对滑动，通常用打滑率表征滑动对履带理论速度带来的影响，数值上常以滑动速度与牵引速度的比值表示，滑动速度大小与履带运动参数有关。

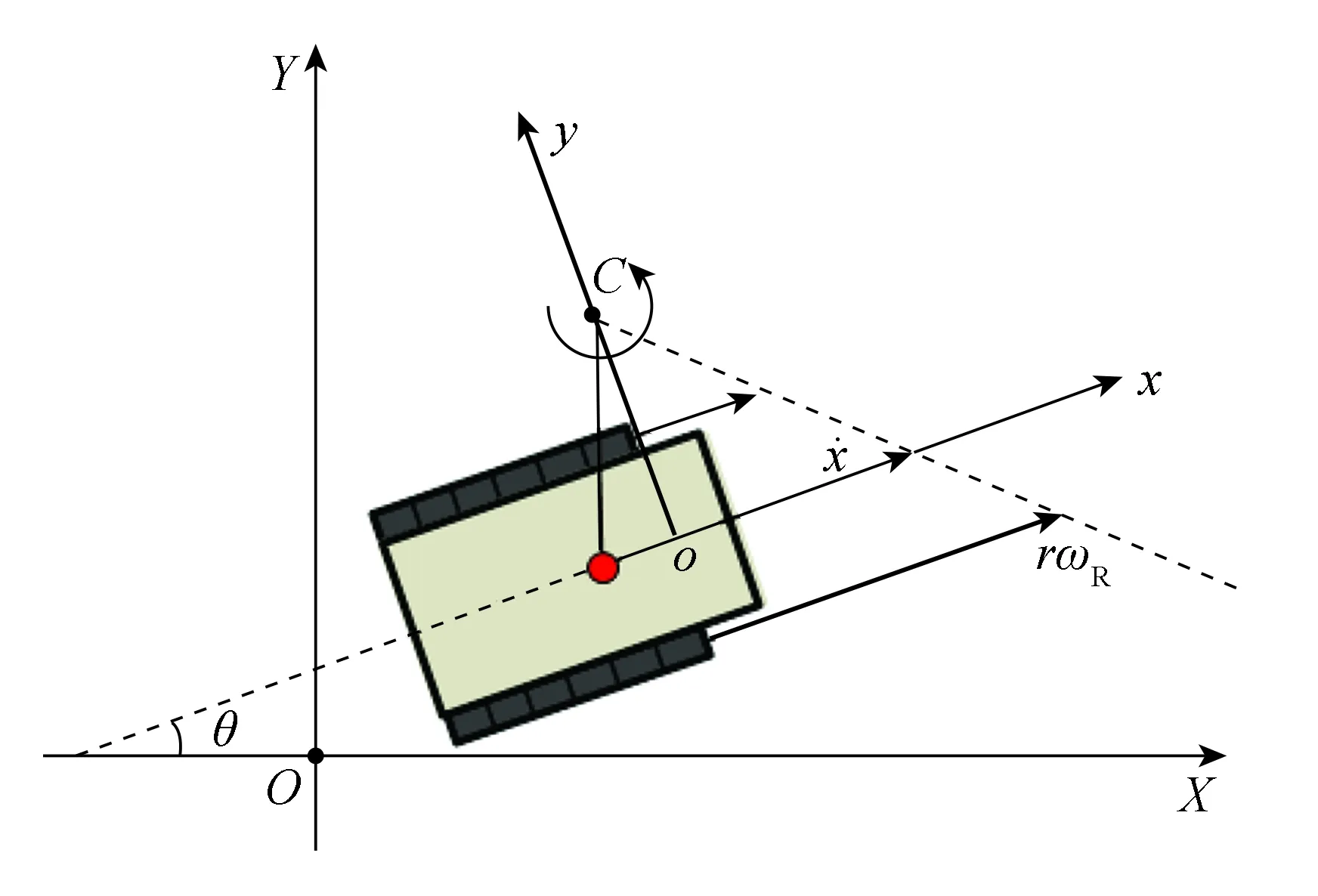
图3 掘进机履带行走运动学模型Fig.3 Schematic diagram of the kinematic model for the road-header

左右两条履带打滑率分别用iL、iR表示。

(8)

以图1所示左转为例，式(8)可变换为

(9)

式(9)表明，若能根据调度目标对机身前进速度与转动角速度进行适当的规划，可进一步演算出对相应的左、右驱动轮角速度的实际数值要求。

2.2 掘进机调度位姿偏差模型

掘进机调度跟踪的偏差模型如图4所示。

图4 掘进机调度跟踪示意Fig.4 Illustration of the position and orientation adjustment for the road-header

图4中以机身当前瞬心到机身中心线的垂足作为分析点(设为机身坐标系xoy的原点)，图中虚曲线表示该点的移动轨迹，为清楚示意机身的移动过程，采用三角形代替机身简化矩形。(x，y)、(X，Y)分别为机身坐标系与大地坐标系中点的坐标值；下脚标c为对应参数的当前值；下脚标d为对应参数的规划值；脚标e为对应参数的当前数值与规划值的偏差。

定义质点当前位姿pc=[Xc，Yc，θc]T、规划或期望位姿pd=[Xd，Yd，θd]T，则质点在机身坐标系xoy中的位姿误差pe=[xe，ye，θe]T可表示为

(10)

对xe取微分，有

(11)

(12)

由图4提出的调度规划轨迹向目标中心线汇合，即可视为掘进机在一定初始偏差状态下需跟踪的行进轨迹，通过逐步调整参数vc、ωc，最终在有限的步数内使得pe有界且趋于0。

3 掘进机行进调度跟踪控制

根据位姿偏差pe=[xe，ye，θe]T的观测结果调整控制参数(vc，ωc)，从而不断减小位姿偏差。显然，由式(10)及式(11)描述的偏差模型是一个两输入非线性系统，可基于Back-stepping设计滑模切换函数。

3.1 掘进机行进调度跟踪控制律设计

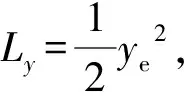
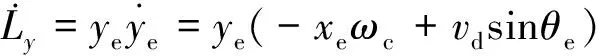
(13)

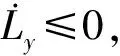
针对由式(10)和式(12)描述的偏差模型，可设计切换函数为

(14)

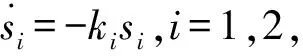
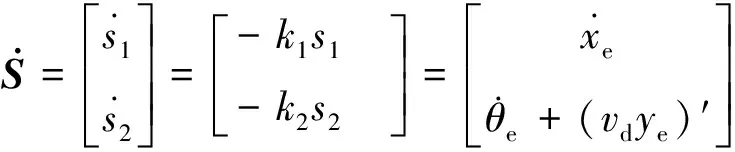
(15)

将式(14)代入式(15)可得

(16)

由式(16)可求解控制律为

u=(vc，ωc)T

为简化控制律结构，考虑到机身转向角速度ωc比其行进速度vc小，且实际运行时vd、xe在数值上远小于1，θe与sinθe同号，将式(16)简化为

(17)

其中，kx、ky、kθ取值为正，分别称为偏差xe、ye、θe的伴随系数或权值。

=xe(vdcosθe-vc+yeωc)+

ye(-xeωc+vdsinθe)+…k(ωd-ωc)sinθe

=-xevc+vdxecosθe+vdyesinθe+k(ωd-ωc)sinθe

(18)

将式(17)代入式(18)可得

vdyesinθe+k(-kθsinθe-vdkyye)sinθe

=-kxxe2+vdyesinθe-kkyvdyesinθe-kkθsin2θe

(19)

若取kky=1，则

由式(17)确定的控制输入能使机身位姿偏差pe逐渐收敛为0。

3.2 掘进机行走动力约束

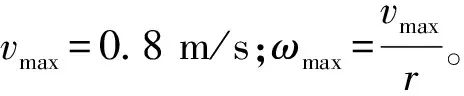
(1) 左、右驱动轮的角速度ωL、ωR同为正(0≤ωL≤ωR)，对式(9)中两等式求导并分别做加减运算可得

(20)

可见，掘进机履带驱动轮角加速度与线加速度互相约束，综合可得

(21)

(2) 当ωL、ωR方向相反(ωL≤0≤ωR)，同理可得

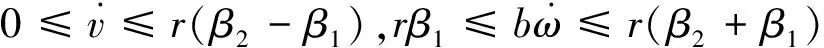
综合可得

第(1)种转向属于大半径转向，其极限工况是一轮制动或以最小转速运转，而另一轮以最大转速运转；第(2)种转向一般用于机身做原地转向调整，此时不可忽略履带侧向打滑。

本文研究的掘进机转向多属于第(1)种情况；当采用控制率函数式(17)计算获得的参数vc、ωc与上一步计算获得的参数vc、wc相比属于第(2)种情况时，将不予采取计算值，而是在限定的范围内就近取值予以替换。

4 仿真与讨论

表2 仿真参数

当目标巷道的中心线位置X=2时，首先根据表1的规划要求设计过渡轨迹。与表1中采用Y=2作为目标中心线相比，由于坐标的对称关系，可直接取表1所列的1号与2号规划轨迹，并将各轨迹上点的X、Y坐标相互调换，方向角θ取其余角代替，如此得到2条调度轨迹，分别记为1*号、 2*号规划轨迹。本次仿真计算中，系数kx、ky、kθ的取值采用试凑法获得，取kx=0.59，ky=0.67，kθ=0.25。

采用1*号规划轨迹实施调度跟踪仿真过程中的机身位姿误差的变化如图5(a)所示，机身中心移动跟踪轨迹如图5(b)所示，左右履带驱动轮转速变化如图5(c)所示。

采用2*号规划轨迹实施调度跟踪的仿真结果如图6所示。

由图5和图6可知，采用不同的规划轨迹，机身在有限的调整周期内位姿误差曲线均趋近于0，跟踪轨迹与规划路径吻合度高。这说明：2种规划轨迹下，机身按式(9)的控制律对行进速度及转角速度进行调整，均能在有限的调整周期内回到期望巷道的位置上；在调度过程中左、右驱动轮的转速差浮动范围基本一致，但就转速自身浮动范围而言，采用1*号规划轨迹要比采用2*号规划轨迹小，且变化相对缓慢。在实际掘进中往往希望驱动轮转速变化范围尽可能小，为避免严重打滑，

图5 采用1*号规划轨迹的跟踪仿真Fig.5 The simulation results when tracking trajectory No.1*

图6 采用2*号规划轨迹的跟踪仿真Fig.6 The simulation results when tracking trajectory No.2*

一般也希望左右轮转速差值尽量小。基于此，仿真所获得的驱动轮转速变化情况将有助于轨迹的合理取舍。

当设置巷道的期望位置Y=2时，利用表1及图2所示的1号规划轨迹进行机身调度跟踪仿真。仿真初始采纳表2的基本参数，且仍取kx=0.59，ky=0.67，kθ=0.25，对应的机身位姿误差的变化和机身中心移动跟踪轨迹如图7所示。

由图7可知，虽然位姿误差在有限的调整周期内均实现趋于0的要求，但在跟踪初期，机身的实际移动轨迹与规划的路径吻合度不太理想。

尝试将系数kx、ky、kθ分别调整为0.1、0.1、0.8后，结果如图8所示。由图8可知，虽然位姿误差xe在相同的调整周期内没能确切地收敛到0，但其呈现不断减小的趋势；同时，跟踪轨迹与规划路径吻合度与图7相比有所提高。这说明轨迹跟踪控制不会因为轨迹上点的X、Y坐标变化不对称而影响最终跟踪目标的达成。轨迹跟踪调度方案可行，但不同的kx、ky、kθ取值可能会造成不同的跟踪效果。

如何根据跟踪目标找出较优的系数组合或动态更替这组系数，以更有效地完成轨迹跟踪，是后继研究内容。