2019年高考江苏卷第12题的解法探究
2020-04-07广东省湛江一中培才学校524037曾肇玲
广东省湛江一中培才学校 (524037) 曾肇玲
向量是解析几何教学中的重要内容,也是高考命题人关注的重要考点之一.其主要考查形式是选择题和填空题,考查内容主要有向量的模、向量的夹角和向量的数量积的计算以及向量平行和垂直的判定等.命题人常通过挖掘“常知”,巧妙构思,编制出新颖独特、内容丰富、形式生动活泼的“考素质,考潜能”令人耳目一新的试题.本文以2019年江苏高考数学试卷第12题为例,探究试题求解历程,追寻命题的溯源,让人人耳目一新、回味无穷,感受数学试题的灵动之美.

图1

1.先入为主——坐标运算法
“先入为主”策略,是指解决平面向量问题时,习惯选择熟悉的坐标运算法.平面向量作为代数和几何的纽带,素有“和平面几何联姻,与代数牵手,与解析几何交汇”之美称.解答平面向量问题时,常“先入为主”,运用“坐标运算法”求解,通过对应点、向量的坐标,结合向量的坐标运算、数量积公式等,让问题柳暗花明.其解题步骤如下:
第一步:“坐标转化”

图2

第二步:“关系探寻”

第三步:“参数转换”

第四步:“消元求值”

2.基底法转化——向量运算法


图3
第一步:关系探寻

第二步:加减转换
第三步:消元求值
此外,还可运用以下几种其他的基底来进行基底法转化求解.

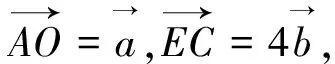





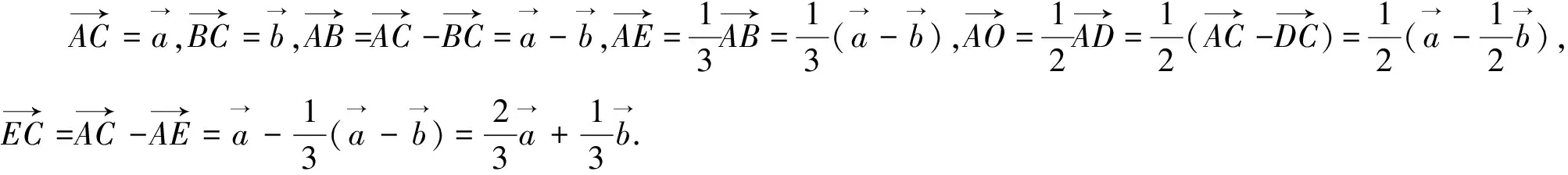

3.前联后挂——逆向溯源法
“前联后挂”是指解决高考平面向量问题时,要研究命题者的组题规律(移植、改换、增减、转化、代替、颠倒、重排)与解题本质,善于运用普遍联系原理与运动变化观点,去考察平面向量内容的知识点之间潜在功能以及其在数学综合知识大系统中相关性、整体性,通过知识点之间演变联合,寻找知识链,形成知识流,架起由已知到未知,由简单到复杂的桥梁.平面向量内容已然成为近几年高考命题的重点和热点,在客观题中大多出现在压轴题位置,其特点是:知识交汇自然,解法灵活多样,但万变不离其宗,紧扣数和形的本质属性来思考和解决问题.其解题“逆向溯源”思维过程如下:
3.1 (组题)基础题源
“源于课本、高于课本、活于课本”是高考命题的基本原则,命题人的视野在不断拓展,这使得他们组题随时都有新的发现.如变更习题(常规题)某些条件,变换思考角度、变化表达方式,进行“貌合神离”或“异曲同工”的改造,引出新问题,发现新方法,扩展了解题思维空间.

图4
此道高考题基础题源为一道经典平面几何试题:如图4,在△ABC中,AD是BC边上的中线,E在AC边上,且AE:EC=1∶2,BE交AD于P,则AP∶PD=( ).
A.1∶1B.1∶2
C.2∶3D.4∶3
高考命题者,通过位置变换,编制为如下高考平面向量“过关”隐含试题:
如图1,在△ABC中,D是BC的中点,E在边AB上,BE=2EA,AD与CE交于点O,试证明:O是的AD中点.
如果考生证明不出“O是的AD中点”这一隐含结论,则学生就需要大量时间进行向量线性变换或坐标转换,也不一定能得出正确答案.
3.2 (命题)逆向溯源



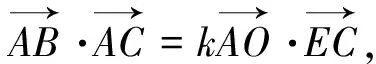
解题反思:高考向量问题,是沟通代数、几何与三角函数的有效桥梁,是通过“数”的运算处理“形”的问题的一种重要方法.主要考查平面向量的基本概念、线性运算、平面向量基本定理、坐标运算、平面向量的平行与垂直的充要条件、数量积及其应用等知识点.命题主要涉及三种类型:一是几何中的全等、平移、垂直等问题转化为向量的运算问题;二是向量的运算问题转化为代数的运算问题;三是三角函数、三角问题转化为向量问题.平面向量内容在高三复习学习时,要学会挖掘高考的潜在作用,善于对试题的联想和构思,横向对比、纵向联系为主,左右对比、前后勾连,提炼出具有普遍性的解题规律,以使自己的知识更加系统化、有序化.
