识模策略在数学问题理解中的运用探析

南通大学理学院 (226007) 钟志华 刘凯峰

认知心理学家西蒙指出：人们在解决数学问题时，大多数是通过模式识别来解决的.首先要识别眼前的问题属于哪一类，然后以此为索引在记忆储存中提取相应的知识，这就是模式识别.

模式识别(Pattern Recognition)是人类的一项基本认知能力或智能，在人的各种活动中都有重要作用.比如一个人观察某个物体并对该物体进行辨认后判断究竟是何种东西，或对所听到的声音进行辨认并确定是何种物体发出的声音，或对某种颜色、气味进行辨认等都涉及模式识别.

在数学学习中，模式识别也普遍存在，小到具体数学问题类型的识别，大到数学概念、数学公式、数学定理以及数学思想方法的运用都离不开模式识别方法.因此，善于运用模式识别方法不仅有助于深刻理解数学的本质，而且对数学问题的解决也具有非常重要的指导意义.笔者曾在“论数学中的模式识别方法”一文中研究了模式识别的机制与类型，本文将进一步探讨运用模式识别方法促进数学问题理解的一些具体策略.

1.识别问题结构

古人云：“不谋全局者，不足以谋一域；不谋万世者，不足以谋一时.”数学问题的理解也应首先着眼于问题的整体结构，即解题者在解题时首先应对整个问题有一个宏观上的理解.这正如美国著名数学家、数学教育学家G·波利亚在《怎样解题》一书中所指出的那样：“首先，我们要将题目作为一个整体来理解.在理解了题目以后，我们在判断哪些特点可能是最重要的内容时，就占据了一个更为有利的位置.在研究了一两个要点以后，我们再判断还有哪些深一层的细节值得研究时，将会占据一个较有利的位置.”事实上，解题者只有首先在整体上对所解决问题的结构有了基本的理解和把握以后才能更好地把握局部，才能少走弯路，而不至于在细节方面迷失方向，出现只见树木，不见森林的现象.具体来说，解题者在解题时首先要对问题整体结构有一个初步的识别或判断，要知道问题的已知条件是什么(起点是什么？)，要求的是什么(目标是什么？)，已知条件与寻求的结论之间有什么联系？有哪些途径或方法可以从起点达到目标？等等，然后在此基础上再进一步深入到问题的具体细节之中.

例1 如图，已知⊙O1，⊙O2相切于P，切线A1C1∥A2C2，B1C1∥B2C2且A1C1⊥B1C1，求证：P，C1，C2共线.

分析：本题中的点C1、C2和切线A1C1、A2C2、B1C1、B2C2一直处在变化之中，如果把眼光仅仅局限于这些具体对象，往往很容易陷入迷局.正确的方法应该是首先跳过具体细节，从大的方面去进行把握，即首先从数学思想方法的高度对问题进行理解或解释：根据图形的特点(两圆相切，这样切点P与两圆圆心O1、O2共线)，我们容易发现可以从变换的观点去考虑问题，将P看作位似中心，⊙O1，⊙O2是以P为位似中心的位似图形，位似将过某点的切线变成过其对应点的切线，这样问题就变得非常清楚了.由于B1C1∥B2C2，可将B1，B2看作是一对对应顶点.

同样地，A1，A2也是一对对应顶点.相应地，B1C1与B2C2是一对对应切线，A1C1与A2C2也是一对对应切线.再根据对应直线的交点也必是对应点，从而就可以知道C1，C2必为对应点.从而P，C1，C2共线.

2.识别关键信息

苏联学者塔尔塔夫斯基曾把数学解题比喻为捕捉躲藏在一堆石头中的老鼠.他说：“有两个方法捕捉躲藏在一堆石头中的老鼠，一是一块一块地抛开石头，直到看见老鼠为止，这时向它扑上去，并且捉住它；二是围绕石头走来走去，并且聚精会神地注视着，是否出现一条老鼠尾巴.一旦发现尾巴就抓住，由石头中抽出老鼠.”模式识别往往也是这样，通过仔细观察发现问题中的关键信息，即解决问题的突破口，然后从此出发求得问题的解决.

例2 在相距105千米的两地A和B，同时相向驶出两个骑摩托车的人，经过1小时45分钟相遇，各人继续沿着自己原来的方向不停前进.3分钟后，以每小时40千米的速度行驶的第一个骑车人在D点遇到了迎面而来的第三个骑摩托车的人.第三个骑车人在和第一个骑车人相遇后也继续沿着原来的方向行驶，并且在C点赶上第二个骑车人.如果第一个骑车人的速度每小时减少20千米，而第二个骑车人每小时增加2千米，那么他们就在C点相遇.问第三个骑车人以什么速度行驶？

3.识别特殊信息

一般来说，不同的问题会表现出不同的特征，而不同的特征往往又会决定着不同的解题思路和解题方法.因此，解题者在解题过程中必须善于通过观察识别问题中出现的各种特征，如数量特征(元素个数、字母的系数或指数等)、结构特征(问题的类型、层次等)、符号特征、关系特征(如大于、小于、等于、平行、垂直等)、位置特征等，然后再利用这些特征的启发与暗示找到解决问题的思路和方法.关于这一点，G·波利亚曾经反复指出，解题者在面对新问题时应不断尝试思考以下问题：“你知道一道与此问题有关的题目吗？你是否知道一道与所解问题具有相同或相似已知量的题目？你是否知道一道与所解问题具有相同或相似未知量的题目？你有没有见到过与所解问题方法相同或相似的题目？你有没有见到过比所解问题更特殊或更一般的题目？”等等.G·波利亚要解题者思考这些问题的目的无非就是要以这些问题来引导解题者发现问题的特征，再将这些特征与解题者头脑中原有的知识(解题经验、解题思路、解题方法等)建立联系并根据这种联系找到求解问题的思路与方法.

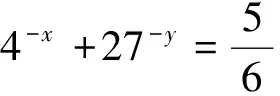
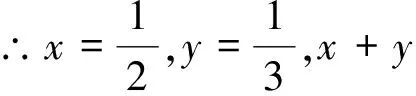
4.识别解题思路(方法信息)

G·波利亚认为：方法就在于按适当的顺序一个接一个地去注意全部有关联的各点.发现解法就是在原先是隔开的事物或想法(已有的事物和要求的事物，已知量和未知量，假设和结论)之间找出联系.然而，事物之间的联系(或解题思路)常常非常隐蔽或似是而非，往往需要解题者对问题的各种要素作深入分析才能发现.波利亚研究表明，不管是新手还是专家，很多时候他们对自己的解题前景或猜想都会有明确的感觉.因此，解题者应对这些或明或暗的思路或猜想进行识别、比较、联想、类比来去粗取精、去伪存真，从而发现比较合理的解题思路.这方面，波利亚介绍了很多宝贵经验，如通过“回归定义”“重新表述问题”“从里面做起”“从外面做起”等策略或通过联想“你有没有见到过与所解问题思路、方法相同或相似的题目？你有没有见到过比所解问题更特殊或更一般的题目？”等方法来发现解题思路.

(1)求数列{Sn}的通项公式；

(2)设{bn}是{Sn}中按从小到大顺序组成的整数数列，①求b3；②存在N(N∈N+),当n≤N时，使得在{Sn}中，数列{bk}中有且只有20项，求N的范围.

5.识别隐蔽信息

美国学者W.A.魏克尔格伦指出，寻找暗含信息往往是解题的关键.对解题者来说十分重要的就是要知道暗含信息究竟属于哪些类型并知道怎样把它们找出来.在数学问题的理解过程中，我们常常有这样的感觉，如果仅仅局限于问题的表面信息往往很难理解问题并找到解决问题的方法，而如果能深入挖掘问题的隐蔽联系则可能会产生“柳暗花明”的感觉.

例5 证明：10022003>2003!.

6.识别无关信息

模式识别不仅要识别有用的信息，同时还要善于将与问题解决无关的信息与有用信息区分开来.

例6 一生物学家为了计算一个湖中的鱼的条数，他想了一个非常巧妙的办法.在五月一日，她随机地捕捉了60条鱼，并对他们作了标记后放回湖中.在九月一日，她再随机地捕捉70条鱼，发现其中3条鱼是有标记的.为了计算五月一日这湖中鱼的条数，她假定五月一日湖中鱼的25%到九月一日已经不在湖中(由于死亡和迁出)，九月一日湖中鱼的40%五月一日时并不在湖中(由于出生和迁入)，而且九月一日抽样所得的无标记及有标记的鱼数是有代表性的.这位生物学家算出的五月一日湖中的鱼数是多少？