注重性质拓展,巧解k值问题
——以反比例函数图像两条性质应用为例
2020-04-07江苏省南京市金陵中学西善分校210041郭源源
江苏省南京市金陵中学西善分校 (210041) 郭源源
近年来,以反比例函数图像为载体的试题,形式多变,结构多样,新颖独特,且蕴藏着丰富的数学思想方法,已然成为了中考的热点问题之一.这类试题主要呈现两个特点:一是“易融性”,双曲线中可以融入各种图形,三角形、平行四边形、矩形、菱形、梯形等无一不在其中,考查双曲线与各种图形的联系,并借助它们的联系求面积或k值;二是“易联性”,以双曲线为主线,关联各种方法,既可用运算较多的解析法求解,也可用思维灵活的面积法求解,兼顾到数和形两种思维特点,综合考查学生的分析问题和解决问题的能力.这类试题不仅可以反映出学生扎实的基本功,还可以体现出创造性的思维品质.本文笔者结合自己在教学中的实践所得,提炼拓展反比例函数图像的性质,并以近些年的中考题为例,谈谈这类拓展性质在解题中的应用,与同仁交流、分享.
一、拓展性质
过反比例函数图像上任意一点,分别向两坐标轴作垂线,则其与坐标轴围成的矩形面积为|k|.这是反比例函数中k几何意义,是最基本的图像性质.与此同时,笔者通过此类题型的研究,还归纳了反比例函数图像中两条拓展的性质.
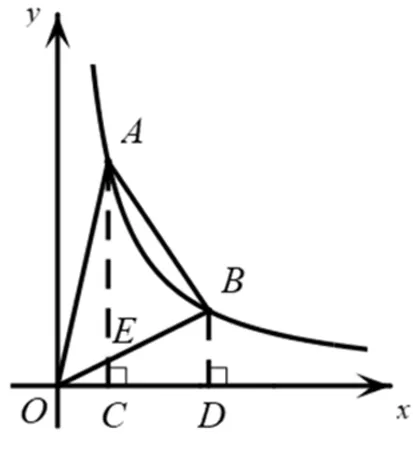
图1
性质1 如图1,点A、B是双曲线上不同的两点,分别过点A、B作x轴的垂线,垂足为点C、D,则S△AOB=
S梯形ABDC.
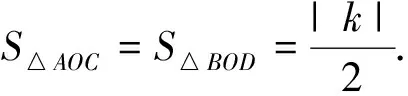

图2

证明:过点A作x轴的垂线,过点B作y轴的垂线,垂足分别是点C、F,AC、BF交于点H,延长EA、DB交于点G.

由相似知识还可以得到AB∥ED.
二、性质应用

图3


点评:平面直角坐标系中求类似于△OAB这样的三角形面积,通常用的是间接求法,以割补法为主.但在双曲线中,这样的三角形可以借助转化,变成直角梯形快速求解.


图4

点评:本题可借助点和点之间的关系,利用参数理出所有点的坐标,再通过面积列方程求解.但若能熟练两个拓展的性质,可直接推理出图形几部分面积的关系,划归面积,求出|k|.


图5

点评:本题条件繁多,图形复杂,然而通过转化划归后,可变成例2的问题模型.△ADE借助平行转化,等积成△ADO,再借助性质1,等积成梯形AFGD,而AC=3DC借助性质2可推理图形几部分的面积比,不需设任何参数就能直接算出k.

图6


点评:本题的分析有两个着眼点,一是点M为矩形对角线的交点,即暗示了点M为GN中点,借助性质2可得到面积比;二是四边形ODBE面积的处理,借助性质1,转化成等积的矩形EFAB.抓住这两点,题目易解.
三、写在最后
反比例函数的k值和面积问题,涉及的知识面广、跨度大、联系紧、综合性强,试题结构新颖且多变,解题方法灵活且多样.要求学生有扎实的数学基本功,能灵活运用所学知识,会多角度思考分析问题.[1]在反比例函数性质的教学中,应抓住最基本最重要的性质,即|k|的几何意义,它是所有k值和面积问题的根本.笔者认为,在探究课本性质的同时,可以带领学生尝试探究反比例函数图像的拓展性质.因为这些性质都是一脉相承,运用拓展性质,掌握好图形面积划归的方法,可以加深对反比例函数本质的理解,从而感悟转化划归、数形结合的数学思想.
一个好的解题方法,应以学生的理解为基础,以解题的高效为动力,以帮助学生全面深刻地看透此类问题为根本,达到“练一题,学一法,通一类”的目标.[2]如本文中的面积转化法,是源于对|k|几何意义的理解,是各项知识的综合运用,可以通解所有此类问题.教学中,题只是知识方法的一个素材,通过解题的过程,理解知识的原理,提炼方法的本质,对比解法的优劣,感悟问题的通性通法.只有这样,解题才能摆脱题海,走向高效.
