探究式教学在习题教学中的应用研究——以一道圆锥曲线问题为例

山东省青岛市胶州实验高中 (266300) 雒义霞聊城大学数学科学学院 (252000) 于兴江

探究式教学被一线教师广泛应用，对教师的教与学生的学都有一定的意义.下面以2019年北京理科卷第18题为例，重点阐述探究式教学在圆锥曲线问题教学中的应用.

(2019北京理科卷第18题) 已知抛物线C:x2=-2py，经过(2,-1).

(1)求C及准线.

(2)设O为原点，过C的焦点作斜率不为0的直线l交抛物线C于M、N，直线y=-1分别交直线OM、ON于点A和点B，求证：以AB为直径的圆经过y轴上的两个定点.

解析:教师在讲解该道抛物线高考题时，首先给学生充分的时间，学生独立思考.第一问中，根据抛物线的定义及相关性质，易得抛物线C的方程为x2=-4y，准线方程为y=1.在第二问中，可证得以AB为直径的圆经过y轴上的两个定点(0,1)和(0,-3).

仔细研究题目发现，(2,-1)是抛物线x2=-4y的焦点，直线l经过(2,-1)，不妨猜想，直线l经过抛物线x2=-4y的焦点.于是引导学生小组之间进行如下探究并给出证明.

图1

图2

于是，学生们不难得到如下结论.

若直线l经过y轴上的任意一点Q(0,b)，则以AB为直径的圆是否会经过y轴上的两个定点呢？小组讨论，师生交流，得到了如下结论.

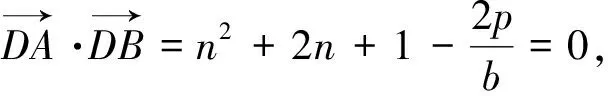
借助于几何画板可以发现直线l过y轴上任意一点的直线.在师生讨论中，不妨探索若另外一条直线为垂直于y轴的任意直线，以AB为直径的圆是否也经过y轴上的两个定点.可得如下定理.

在以上探究、结论及定理的研究过程中发现:以AB为直径的圆经过y轴上的两个定点与垂直于y轴的任意直线与y轴的交点有关.在探究教学中，学生学会了探究的思想，不难提出如下猜想.

猜想抛物线以x轴为对称轴，直线l经过x轴上的任意一点Q(m,0)，另一条直线为垂直于x轴的任意直线时，是否还有相关的结论呢？

若把圆换为椭圆时，结论是否还会成立呢？可得到如下定理.

图3

将定理1和定理3进行优化，可得到如下定理.

可以发现定理4中的条件与结论互为充分必要条件，最终可得到如下定理.

就如托尔斯泰所说，“成功的教学所需要的不是强制,而是激发学生的学习兴趣.”教师要将探究式教学应用到习题教学中，培养学生探究创新的能力.