管窥2019年浙江高考第21题
2020-04-07浙江省宁波市第四中学315016蒋亚军
浙江省宁波市第四中学 (315016) 蒋亚军
1.题目呈现
如图1,已知点F(1,0)为抛物线y2=2px(p>0),点F为焦点,过点F的直线交抛物线于A、B两点,点C在抛物线上,使得△ABC的重心G在x轴上,直线AC交x轴于点Q,且Q在点F右侧.记△AFG,△CQG的面积为S1,S2.
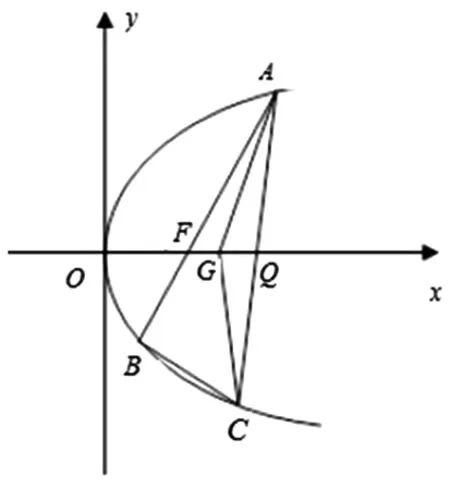
图1
(1)求p的值及抛物线的准线方程;
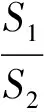
2.解法剖析
2.1 抓住抛物线的属性
解法1:设直线AB的方程为x=ty+1(t>0),其中A(x1,y1),B(x2,y2),与抛物线方程y2=4x联立可得y2-4ty-4=0,故y1+y2=4t,y1y2=-4.
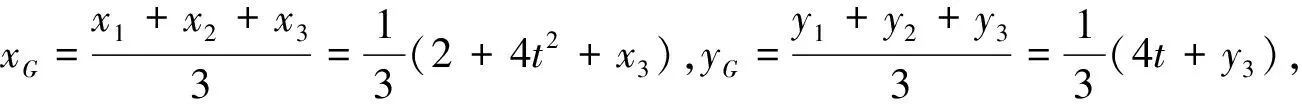
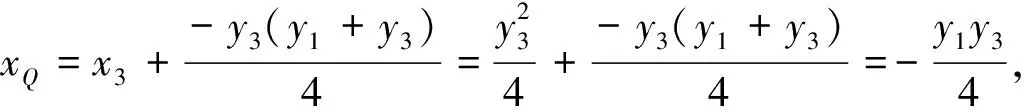
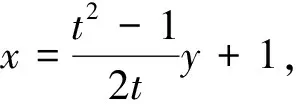

评注:上述二种解法是解析几何的常规方法,解法1利用相关条件,从联立抛物线与直线方程入手;解法2通过设点建立起它们之间的联系,虽然说是通性通法,考虑到变量比较多,统一转换为A点的纵坐标t,对学生数学运算能力的要求比较高.
2.2 挖掘三角形的性质
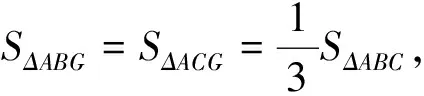

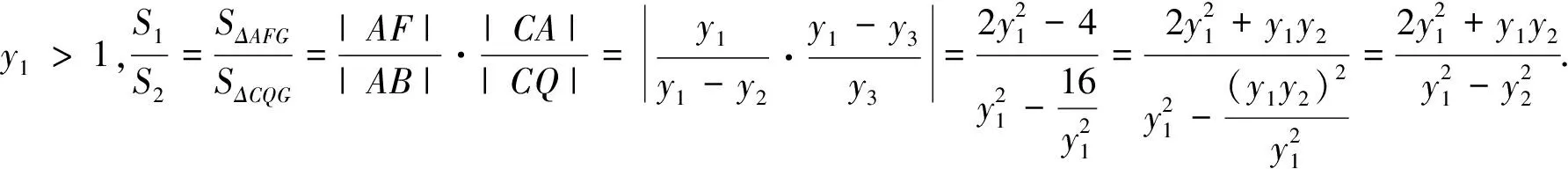


2.3 借助向量共线定理

评注:解法6依托平面向量基本定理及三点共线,将三角形面积之比等价转化为系数之比,使得问题转化为学生所熟悉的基本不等式型求最值问题.该解法有效地避免了三角形面积的繁琐计算和复杂的表示,可谓是运算的第三层次.
3.几点感悟
3.1 研究试题命制,感悟核心素养
纵观上述试题的研究,其一:充分体现试题的层次性,第(1)注重基础,重点考查基础知识;第(2)难度逐步提升,让各个层次的学生都有所获,通过设计动点或动直线问题,重点考查学生综合运用知识解决数学问题的能力,让学生充分感悟逻辑推理、数学运算、数形结合思想在本题中的渗透,体现能力立意.这促使教师在教学中,要重视解题过程的演示,学生要重视对解题过程的体验,这样不仅能巩固相关知识点,还有助于逻辑推理和数学运算素养的构建,也提升了学生提出和发现问题、分析和解决问题的能力.[1]其二:彰显数学建模的重要性,本题的基本模型是平面几何中“燕尾定理”,将这个三角形构建在抛物线上,同样我们将这个三角形构建在椭圆或双曲线上,得到相关的试题(如图2,图3所示).
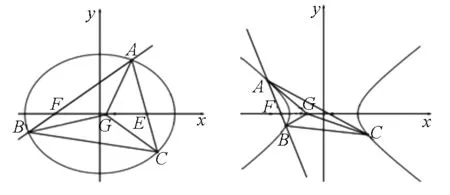
图2 图3
3.2 探究试题解答,体现核心素养
通过对解析几何解答题的深入研究,分析其典型试题的试题命制、解答过程、探究推广,能更具象化地揭示其所蕴含或要求的核心素养,帮助学生弄清问题的本质,追本溯源,注重思路的产生过程,也有利于强化培养学生数学核心素养的理念.
