对一道三棱锥外接球高考题的解法探究

江西教育传媒集团 (330038) 周瑜芽

棱锥的外接球问题，特别是三棱锥的外接球问题，是高中各类考试中的常见题型，此类题型主要考查三棱锥外接球的体积或表面积的求解.解决这类题的关键在于求出三棱锥外接球的半径，即找到球心所在的位置.笔者下面以一道2019年全国高考试题为例，探究三棱锥外接球问题的解法，供大家参考.

一、题目 (2019年高考新课标Ⅰ卷理)

已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为().

二、解法探究

法1：补形法

如果三棱锥其中一个侧面与底面垂直，还原不到特殊图形中去，可以想到利用补形成为直棱柱，利用棱柱的性质进行解题.常见的补形方法有：正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补形成长方体或正方体；同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥，可将三棱锥补形成长方体或正方体；若已知棱锥含有线面垂直关系，则可将棱锥补形成长方体或正方体；若三棱锥的三个侧面两两垂直，则可将三棱锥补形成长方体或正方体.

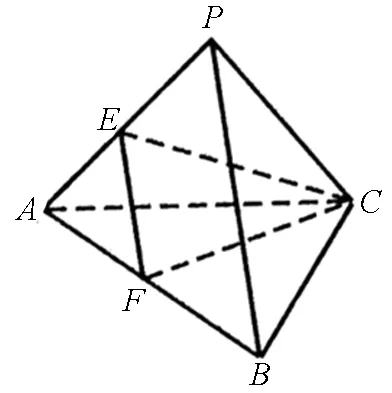
图1

解析：如图1，设PA=PB=PC=2x，在ΔPAC中，由余弦定理知cosA=

点评：方法1是用余弦定理求得CE的长，通过勾股定理发现了共顶点的三条棱相互垂直，从而构造了正方体，这样求外接球的表面积或体积更简捷.

法2:截面法

解决与球有关的“切”“接”问题，一般要过球心及多面体中的特殊点或过线作截面，把空间问题转化为平面问题，从而寻找几何体各元素之间的关系.利用长方体、三棱锥的性质、三棱锥底面外心或侧面外心、过三棱锥的底面上一边作对棱的截面，则可简化运算，巧妙探索外接球球心或半径.

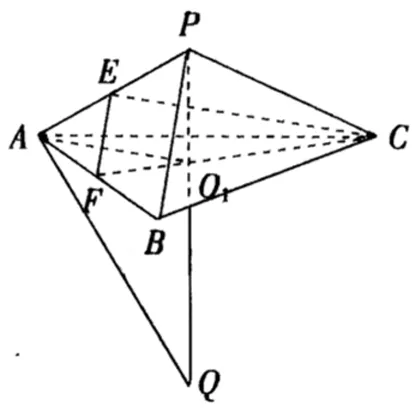
图2

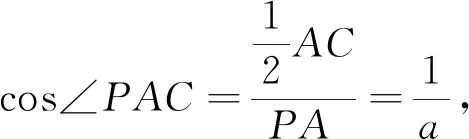
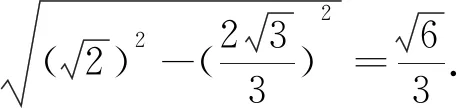
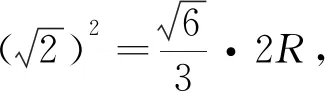
点评：方法2主要抓住PA=PB=PC的对称几何特征，选择Rt△APO1所在平面为截面进行降维处理，利用Rt△PAQ这个特殊平面图形结合射影定理求得球的半径R，进而求球的体积.

三、试题链接

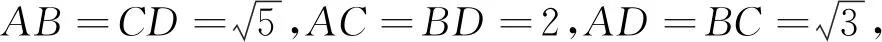
4．(2019·湖南长沙市实验中学高三月考)《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P-ABC为鳖臑，PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上，则球O的表面积为( ).

A．8πB．12πC．20πD．24π

(参考答案：1.D;2.B;3.C;4.C)