双重障碍物对开闸式异重流运动特性的影响

林颖典，韩东睿，袁野平，贺治国

（浙江大学海洋学院，浙江舟山316021）

异重流（gravity current），又称密度流（density current）或者浮力流（buoyancy current），其是在重力场作用下，2种流体的密度差异造成水平压力梯度，从而产生相对运动的现象［1］。在自然环境和水利工程中，异重流现象广泛存在［2］。根据形成密度差异的原因不同，异重流可分为两类：成分驱动异重流（如河口盐水入侵）和颗粒驱动异重流（如浊流）［3］。现实工况中，异重流的侵袭会造成巨大的危害，如据报道，海底浊流（颗粒驱动异重流）导致水下峡谷侵蚀以及破坏海底电缆［4］，海水淡化厂的污水排放（成分驱动异重流）对周围环境（如湿地）造成污染［5］等。障碍物的设置可以显著改变异重流的运动特性［4］，如在大型水库中，泥沙淤积会减小其有效库容，在底床设置障碍物能够改变泥沙的沉积-悬浮状况，防止泥沙沉积在关键部位，则可延长水库的寿命［6］。

水利工作者越来越关注地形和障碍物对异重流运动特性的影响［7］。由于野外原位观测需要消耗大量的人力和物力，实验室水槽模拟实验已经成为研究异重流的主要手段［8］。前人的工作主要集中在单一障碍物对异重流运动影响的研究，如Woods等［9］发现异重流遇到障碍物时会在其上游形成移动的反射水跃；通过地形的改变，范家骅［10］分析了伴有局部水体掺混的异重流内部水跃上下游水力因子之间的关系，并利用动量方程和连续方程推导了包含上下层流体之间水量掺混的内部水跃理论表达式；Greenspa等［11］指出障碍物的形态对异重流的越障能力有显著的影响；Asghari等［12］通过系列水槽实验，提出完全阻塞异重流时的量纲一化障碍物高度；Oehy 和Schleiss［13］通过水槽实验推断出，在底床设置一个20m的障碍物可以将小型水库（库容不小于100万m³）的使用寿命延长50年；Oshaghi等［14］通过室内水槽实验研究了入流弗劳德数与异重流越障性能的关系：入流弗劳德数越小，异重流运动对障碍物的存在越敏感；Wilson等［15］研究了浊流遇到单一矩形障碍物时与环境流体的卷吸掺混过程，发现异重流在障碍物下游的掺混显著加剧。近几年，亦有少部分国外学者对双重障碍物的影响机制展开研究（如Kubo［16］、Yaghoubi等［17］），但是关注点主要集中在障碍物对泥沙沉积特性的影响，少有对双重障碍物最优工程布置方案的探讨。

因此，本文利用水槽实验手段，选用开闸式出流方式，结合双重障碍物间距和高度2个变量，对成分驱动异重流流经双重障碍物的动力学特性进行研究。实验采用数码相机记录异重流的演变过程，结合粒子图像测速技术（particle image velocimetry，PIV），分析障碍物上下游区域的异重流速度剖面，对比不同障碍物间距及高度对异重流最大扩散高度、头部速度等方面的影响，对比无障、单一障碍物、双重障碍物工况对异重流掺混系数的影响，从而得到双重障碍物的最优工程布置方案。

1 实验设置

1.1 实验装置和步骤

实验水槽长200 cm、宽20 cm、高20 cm（如图1）。水槽长宽比等于10可以将异重流简化为二维运动［8］。实验中闸门通过步进电机控制启闭，以消除人工启闭引起的扰动影响。实验水槽闸门右侧的闸室（长L0=9.5 cm）内注入盐水模拟异重流，闸门左侧注入清水生成均匀环境水体，环境水体水深和闸室内盐水水深均为H=15 cm。闸室内盐水以适量染色剂（食用色素）染色。

Huppert和 Simpson［18］最早提出开闸式异重流的运动过程：异重流从闸门释放后首先会经历2～4倍闸室长的加速阶段，然后会以定常速运动至8～10倍闸室长处（坍塌阶段），最后进入减速阶段（自相似阶段和粘性阶段）。第一障碍物放置在距离闸门L1=5L0处，保证异重流遇到障碍物前发展为定常速流动，第二障碍物与第一障碍物的间距设置详见第1.2节。闸门开启后，盐水进入环境流体中，沿着实验水槽底部向前运动，盐水和环境水体形成典型对流运动［19］，当异重流到达实验水槽末端后实验结束。实验中以帧率为25 fps的彩色数码照相机记录异重流的行进过程、形态结构等。采用帧率为100 fps的PIV拍摄系统记录异重流流经障碍物时的局部过程，并结合PIVlab［20］提取特定位置的异重流垂向速度数据。

1.2 参数设计和实验工况

异重流与环境流体之间密度的差异导致浮力梯度的存在［1］，用约化重力加速度描述该密度差异，为

式中：ρc为异重流密度，；ρa为环境水体密度；g=9.81 m·s-2为重力加速度。

量纲为一的雷诺数和弗劳德数可表示流体的流态特征，此处定义的异重流总体雷诺数Re0、总体弗劳德数Fr0、密度弗劳德数Frd［21］如下：

图1 异重流实验水槽设置（单位：mm）Fig.1 Setup of the experimental flume for gravity current（unit：mm）

量纲为一的理查森数可表征异重流与环境流体的掺混特性，此处定义异重流理查森数为［22］

表1为异重流实验工况及参数。所有工况盐度s皆设为3.4%，其密度ρc为1 024 kg·m-3，障碍物断面为等腰三角形，其底边长度为2.5 cm。2个障碍物皆有3 cm和5 cm这2种高度，共计4种高度组合（即3-3，3-5，5-5，5-3），第一障碍物与第二障碍物的间距L2分别等于1L0，2L0，3L0，5L0（即9.5，19，28.5，47.5 cm），设置无障碍物工况和单一障碍物工况为対照组。实验中各组总体雷诺数均大于2 000，认为异重流流态为湍流，可忽略粘滞力对异重流的影响［8］。此外，实验中各组总体弗劳德数均小于1，故实验工况条件下，异重流为缓流。

表1 实验工况及相关参数Tab.1 Experimental cases and parameters

Asghari等［12］根据量纲为一的障碍物高度（H1/ht）和总体弗劳德数将异重流的越障情况分为4个区域（如图2）。其中Ⅰ、Ⅲ区分别表示异重流以缓流和急流的形式完全通过障碍物，Ⅳ区表示障碍物完全阻滞异重流，Ⅱ区表示一部分异重流通过障碍物，另一部分异重流以反射水跃形式向上游传播。结合现实工况，主要对Ⅱ区异重流的运动特性展开研究。

图2 异重流越障分区Fig.2 Motion regions for gravity current over obstacles

2 结果分析

2.1 形态分析

图3为开闸式异重流流经双重障碍物的发展过程。闸门开启后，异重流前端形成典型半椭圆状的头部形态，如图3a所示，其后为主体段和尾部段。由于异重流与环境流体之间剪切不稳定性［18］，异重流的主体段上方形成开尔文·赫姆霍兹涡（Kelvin-Helmholtz Billows，简称K-H涡）。

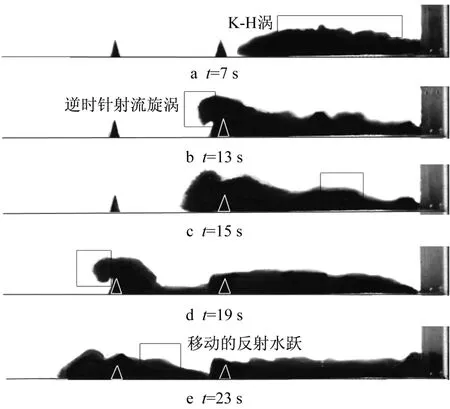
图3 异重流流过双重障碍物发展过程（工况12）Fig.3 Propagation process of gravity current over two consecutive obstacles(case 12)

如图3b、3c所示，当异重流遇到第一障碍物时，一部分异重流以反射水跃的形式向障碍物上游方向移动，直到其传播到闸门处，第一障碍物上游区域的异重流流态为缓流（Frd＜1，见图6）；另一部分的异重流以射流的形态越上障碍物，其头部形成逆时针旋涡。由于密度逆分层而导致的瑞利-泰勒不稳定性（Rayleigh-Taylor instability）［23］以及约化重力加速度的作用，异重流头部急速下潜回底床，其厚度变大，需要一定扩散距离来恢复典型头部形态，之后沿底床向第二障碍物运动。当异重流遇到第二障碍物时，其越障过程与第一障碍物相似。如图3d、3e，一部分异重流以反射水跃的形式向第一障碍物传播，直到其传播到第一障碍物下游处，两障碍物之间区域的异重流流态为缓流；另一部分的异重流越过障碍物之后流态为急流（Frd＞1，见图6），此时发生水跃现象，头部厚度变大，速度减缓，流态由急流变为缓流。

根据异重流运动形态不同，其越障过程可分为4个不同阶段：纵向收缩阶段：主流流速急剧下降，在g′作用下，异重流头部抬升；射流阶段：异重流以射流形态离开底床，其头部形成逆时针旋涡；坍塌阶段：该阶段异重流的运动形态与闸门开启后的重力坍塌相同；形态重塑阶段：是异重流越障后恢复其越障前形态的过程，其头部上方形成较大的顺时针KH涡。

2.2 工程最优解

在异重流防护工程中，合理的布置障碍物，不仅可以提高工程效率，还可以节约成本。双重障碍物的布置方案应有效削减异重流的侵袭速度，并尽可能减小异重流在环境流体中的扩散范围。双重障碍物布置参数主要包括间距设置及高度组合。

图4为障碍物间距与异重流运动参数关系图。在障碍物高度组合固定的情况下，越过第二障碍物后的异重流速度减幅呈现先增大后减小的趋势，并在障碍物间距L2设置为2L0～3L0时取得最大速度减幅（如图4a）。随着障碍物间距L2的增加，异重流在环境流体中的最大扩散高度逐渐减小（如图4b），究其原因：障碍物间距的增加，致使更多体积的异重流被阻滞在两障碍物中间区域，越障的异重流体积相对减少，其最大扩散高度减小。对于单一障碍物工况，异重流越障后的头部形态的重塑距离大致为2L0～3L0［9］。结合图 4a可知：若异重流在遇到第二障碍物前未完成头部形态的重塑，其越障后的速度减幅要大得多。此外，考虑到异重流在两障碍物间形成的移动水跃会对障碍物造成二次撞击，故两障碍物的最优间距L2=3L0。

图5为在最优障碍物间距（L2=3L0）条件下，障碍物高度组合与异重流最大扩散高度的关系。表2为在最优障碍物间距（L2=3L0）条件下，异重流越过第二障碍物的速度。由图5可知：设置障碍物会显著增加异重流在环境流体中的最大扩散高度。由表2可得：高障碍物对异重流的阻滞效果明显强于低障碍物，对比工况10和18，先高障碍物后低障碍物的高度组合效率更佳。究其原因：第一障碍物的高度决定了上游反射水跃的体积，当其高度不足时，无法形成有效的反射水跃，对异重流侵袭的阻滞无效。

综合考虑障碍物的阻滞效果、异重流在环境流体中的扩散范围及工程成本，最优布置方案为：第一障碍物高于第二障碍物，同时第一障碍物的高度要保证异重流在其上游区形成明显的反射水跃；障碍物间距要尽可能大（L2=3L0），应保证异重流遇到第二障碍物前未恢复典型头部形态，同时减小移动反射水跃对障碍物的二次撞击。

2.3 掺混特性

分析异重流的掺混特性对进一步了解异重流的动态演化过程有重要作用［24］。Jacobson和Testik［25］通过考虑二维侧面积变化定义异重流平均掺混速率we，表达式如下

图4 障碍物间距与异重流运动参数关系Fig.4 The relationship between obstacle spacing and motion parameters of gravity current

图5 障碍物高度与异重流最大扩散高度关系Fig.5 The relationship between obstacles height and maximum diffusion height of gravity current

表2 第二障碍物下游异重流头部速度对比Tab.2 Comparisons of head velocity of gravity current in the downstream of second obstacle

其中：uf为异重流头部速度；xf为异重流头部位置；A为开闸式异重流的二维侧面积。

结合 Wilson等［15］和Ottolenghi等［26］的方法，用掺混系数E来描述异重流与环境水体的掺混情况，其定义为

图6为异重流掺混系数E的沿程变化图。其中量纲为一的异重流头部位置x*=xf/H。由图可见：无障碍物工况，异重流的掺混系数稳定在0.05左右。当障碍物存在时，越障过程中异重流的掺混系数沿程出现“M”型分布。纵向收缩阶段，异重流头部受障碍物限制，其厚度增加，故dA/dx变大，uf急剧减小，E相应变大，之后在约化重力加速度g′作用下，异重流头部抬升，水平速度分量增加，E相应变小；射流阶段由于异重流的旋涡状头部迅速膨胀，dA/dx变大，E呈现增大的趋势；坍塌阶段，由于密度逆分层和g′作用，异重流加速下潜，uf急剧增大，E呈现减小趋势。

图6 掺混系数E沿程变化Fig.6 Changes in the entrainment coefficientE along the channel

此外，完成形态重塑阶段的异重流，工况3（单一障碍物）的掺混系数E稳定在0.060左右，工况18（最优解）的掺混系数E稳定在0.075左右，皆大于相同位置的无障碍物工况1。障碍物的存在，改变了障碍物附近的掺混机制，并强化了障碍物下游的掺混，使异重流更快被稀释，其侵蚀范围变小。

Turner［27］发现异重流掺混速率和理查森数Rig成负相关。图7给出异重流沿程的密度弗劳德数Frd和理查森数Rig变化。异重流越过第一障碍物前后，理查森数Rig相差不大，所以第一障碍物对异重流掺混速率的影响相对较小。当异重流越过第二障碍物后，理查森数明显减小，异重流的掺混速率显著增加。由此可见，实际异重流防护工程中，第二障碍物的设置是必要的。

图7 Frd和Rig沿程变化图Fig.7 Changes in the Frdand Rigvalues along the channel

2.4 速度剖面和涡度场

异重流速度剖面以速度峰值点为界，分为壁面区（wall region）和射流区（jet region）［28］。 根 据Altinakar等［28］的经验公式，速度剖面可表征为

其中：um和hm为速度峰值和该峰值点距底床的高度；αv、βv和γv为经验系数。

为验证实验结果，采用式（8）、（9）与本实验异重流的速度剖面（通过PIVlab提取异重流速度数据）拟合结果相比较，如图8所示，图中断面距离闸门50 cm，数据样本时间间隔0.2s）。表3为本实验拟合结果和Altinakar等［28］的经验系数对比。可以发现，经验系数αv和γv相差不大，但βv却有较明显差别。因Altinakar等实验的异重流的总体弗劳德数为1.00～2.33，入流方式为持续入流，而该实验的总体弗劳德数为0.6左右，入流方式为开闸式入流，所以经验系数的差异是合理的。

图9中数据样本时间间隔0.2 s。如图9a所示，在障碍物上游区域，相比于无障工况，障碍物的存在使异重流速度剖面出现畸变，其畸变的范围大致与障碍物等高，主流速度明显减弱。在障碍物下游区域（图9b），完成形态重塑阶段的异重流，其速度剖面均存在明显的壁面区和射流区，相对于无障和单一障碍物工况，流经双重障碍物的异重流速度峰值衰减了近乎一半，并且异重流厚度明显变小。

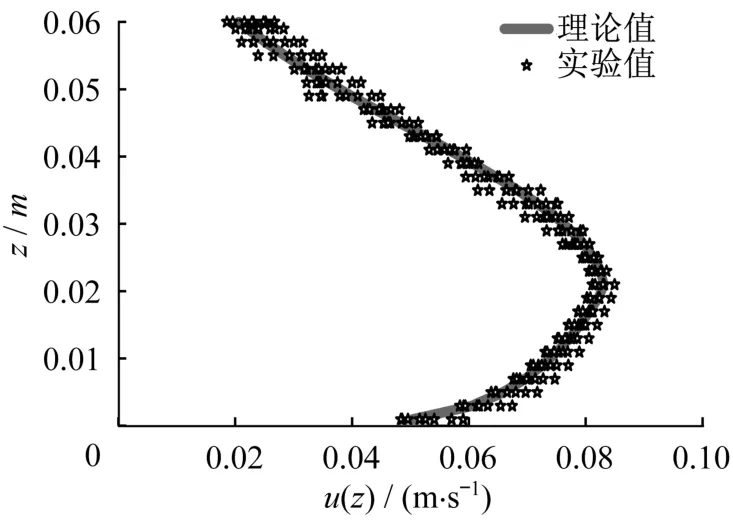
图8 无障碍物工况1时异重流速度剖面图Fig.8 Vertical velocity profile of gravity current

表3 经验系数对比Tab.3 Comparison of the empirical constants

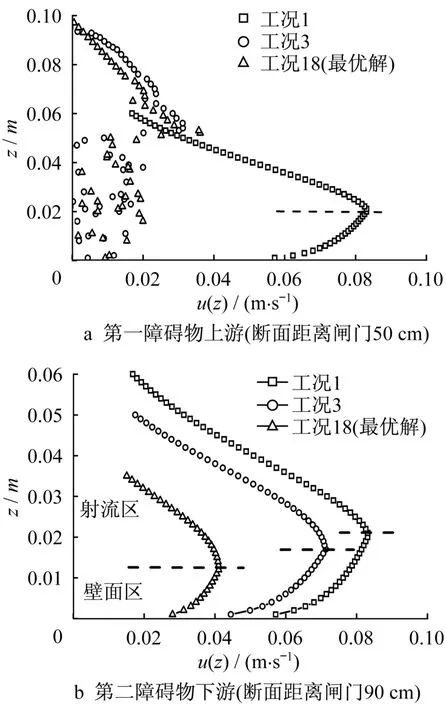
图9 异重流速度剖面图Fig.9 Vertical velocity profile of gravity current

图10给出最优解工况下异重流越过2个障碍物时0.2 s（20张PIV图像）内的平均涡度场。涡度计算公式为w=∂u/∂z-∂w/∂x［8］，其中x和z为异重流主流向和垂向，u和w为异重流瞬时的主流和垂向速度。涡度正负代表方向：顺时针为正，逆时针为负。如图10a所示，异重流越过第一障碍物时，其上边界与环境流体间因湍动作用引起的K-H涡和斜压不稳定性（密度与压力梯度不平行）而出现正向涡度值，在下底床边界，由于固体边壁条件以及底床粘性作用产生负向涡度。此外，射流态的异重流在约化重力作用下，其头部区域出现负向涡度最大值（逆时针旋涡），大量环境流体被卷吸进异重流内部。当异重流遇到第二障碍物时，由于其头部未完成形态的重塑，越障过程中正向负向涡度分布趋向无序，异重流头部区域的负向涡度最大值更大，尺度更小（相对于第一障碍物），其与环境流体掺混更加剧烈。

图10 工况18最优解时异重流在0.2内的平均涡度场Fig.10 The average vorticity field in 0.2s（case 18）

3 结论

通过双重障碍物对开闸式异重流运动特性影响的系列实验研究，主要结论如下：

（1）根据异重流运动形态的差异，其越障过程可分为4个不同的阶段：纵向收缩阶段、射流阶段、坍塌阶段、形态重塑阶段。异重流遇到障碍物时能否形成明显的反射水跃决定了该障碍物是否有效。

（2）综合考虑障碍物的阻滞效果、异重流在环境流体中的扩散范围及工程成本，最优布置方案为：第一障碍物高于第二障碍物，同时第一障碍物的高度要保证异重流在其上游区形成明显的反射水跃；障碍物间距要尽可能大（L2=3L0），应保证异重流遇到第二障碍物前未恢复典型头部形态，同时减小移动反射水跃对障碍物的二次撞击。

（3）无障碍物工况，异重流的掺混系数稳定在0.05左右。当障碍物存在时，越障过程中异重流的掺混系数沿程出现“M”型分布。异重流越过障碍物后的掺混速率大于无障碍物工况，其中双重障碍物工况大于单一障碍物工况。

（4）在障碍物上游区域，相比于无障工况，异重流速度剖面出现畸变，其畸变的范围大致与障碍物等高，头部前行速度明显减弱。在障碍物下游区域，完成形态重塑阶段的异重流，其速度剖面均存在明显的壁面区和射流区，相对于无障工况，流经双重障碍物的异重流速度峰值衰减了近乎一半，并且异重流厚度明显变小。

（5）异重流越过第一障碍物时，射流态的头部在约化重力作用下，该区域出现负向涡度最大值（逆时针旋涡），大量环境流体被卷吸进异重流内部。当异重流遇到第二障碍物时，由于其头部未完成形态的重塑，越障过程中正向、负向涡度的分布趋向无序，异重流头部区域的负向涡度最大值更大、尺度更小（相对于第一障碍物），其与环境流体掺混更加剧烈。