绿色纳米零价铁为催化剂的类芬顿法降解甲基橙

李赛，田瑜，徐婷婷，郭波

(太原理工大学 环境科学与工程学院，山西 晋中 030600)

我国印染行业在近年来迅速发展，偶氮染料约占合成有机染料中70%[1]。这类废水具有降解性差、致突变性和致癌性差等特点[2-3]。

近年来，Fenton法是一种广泛应用于水处理的高级氧化工艺，它以亚铁盐为催化剂，催化H2O2释放强氧化性的·OH[4]。此法存在铁盐利用率低，pH应用范围窄等问题[5-6]。本文采用绿色合成纳米零价铁作为类芬顿体系催化剂，利用纳米粒子自身优势，Fe3+在nZVI表面被还原为Fe2+，同时扩大pH的应用范围[7]。本文利用GS-nZVI/H2O2类芬顿体系降解偶氮染料甲基橙(MO)。

1 实验部分

1.1 材料与仪器

甲基橙、H2O2(30%)、七水合硫酸亚铁、硫酸、氢氧化钠、无水乙醇均为分析纯；葡萄籽，取自市售葡萄的废弃物。

UV-1900PC紫外可见光分光光度计；HJ-4A数显多头磁力加热搅拌器；pHS-3C精密pH计；GZX-9076 MBE数显鼓风干燥箱；HH-S6数显恒温水浴锅；H1650R离心机。

1.2 GS-nZVI制备

制备方式见李美玲等[8]使用葡萄籽提取液与二价铁盐制备GS-nZVI悬浊液。

1.3 实验方法

取100 mL一定浓度的MO溶液于250 mL锥形瓶中，调节pH，将锥形瓶置入恒温振荡箱中，加入一定量的GS-nZVI悬浊液和H2O2(10%)，将锥形瓶封口后于振荡箱(250 r/min)中进行反应。每隔一定时间测定MO的浓度。分别考虑溶液pH、反应温度、MO初始浓度和H2O2浓度对降解效果的影响。

1.4 分析方法

采用分光光度法，在波长465 nm下测定MO的吸光度，计算浓度，并通过计算降解率显示降解效果。降解率=(1-Ct/C0)×100%。式中，C0为MO初始浓度，mg/L；Ct为降解MO在tmin的浓度，mg/L。

2 结果与讨论

2.1 对比实验

在初始溶液pH为6.8(不调整pH值)，温度35 ℃下，在 100 mL的100 mg/L MO溶液中，分别加入1 mL GS-nZVI悬浊液、20 mL H2O2(10%)以及1 mL GS-nZVI悬浊液+20 mL H2O2(10%)，考察3种情况下的MO降解效果。结果如图1，反应180 min，单独加入GS-nZVI和H2O2时MO的浓度变化很小，MO去除率分别为9%和5%。与GS-nZVI/H2O2类芬顿法降解MO效果相比，GS-nZVI、H2O2单独对MO的降解效果可以忽略不计，因此降解过程是由类芬顿体系主导的。

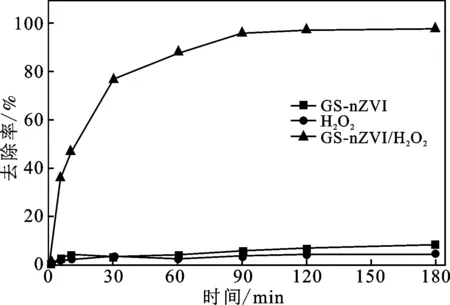
图1 GS-nZVI、H2O2和GS-nZVI/H2O2对MO降解效果的比较

2.2 影响因素对降解效果的影响

2.2.1 pH对降解的影响 取100 mL 100 mg/L MO溶液，分别调节溶液pH为3，5，7，9和11，然后加入1 mL GS-nZVI悬浊液和20 mL H2O2(10%)，35 ℃时，考察不同pH值对MO降解的影响。结果见图2，pH值对MO的降解效果随着pH值的增大而变差。但pH=3，5，7时，类芬顿法对MO的降解效果变化不大，在反应90 min后，降解率均达到95%以上。芬顿或类芬顿法均通过反应过程中产生·OH降解污染物，·OH的电位随pH值的降低而增大，氧化能力增强，从而能够更有效地降解MO[7]。传统芬顿法适用pH为3～4，狭窄的pH使用范围限制了此方法的应用，而类芬顿法，如在GS-nZVI/H2O2体系中，产生·OH的反应主要发生在nZVI粒子的表面，因而受到体相溶液pH的影响较小，pH的适用范围得到扩大[7]。在相同条件下，pH为6.8～9范围内，分别采用GS-nZVI/H2O2类芬顿法和传统芬顿法降解MO的效果比较如图3所示。其中初始溶液pH=6.8，不需调节pH。从图中可看出，pH在6.8～9范围内，反应60 min后，GS-nZVI/H2O2类芬顿法降解MO的效果显著优于传统芬顿法，如pH=6.8，反应120 min，类芬顿法和传统芬顿法对MO的降解率分别达到97.86%和71.84%。

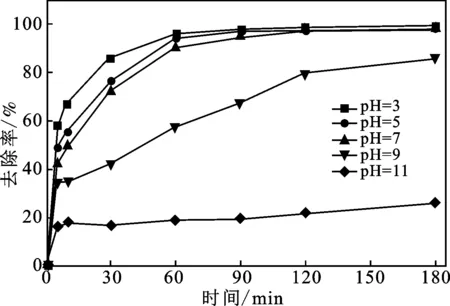
图2 pH对MO降解效果的影响

图3 芬顿法与GS-nZVI/H2O2类芬顿法对MO降解效果的影响

2.2.2 反应温度对降解效果的影响 取100 mL 100 mg/L MO溶液，加入1 mL GS-nZVI悬浊液，溶液pH=6.8(不调节pH)，随后加入20 mL H2O2(10%)溶液。考察温度25，30，35，40 ℃下MO的降解效果。

图4 反应温度对MO降解效果的影响

由图4可知，随反应温度的升高，MO的降解率提高。在反应180 min时，25，30，35，40 ℃的降解率分别达到91.46%，95.83%，97.86%，98.81%。在降解过程中，随着反应温度的升高，溶液中粒子热运动加剧，提高了各反应物质的接触几率，使得nZVI激活H2O2释放更多·OH，使得染料的降解效果提高。

2.2.3 染料初始浓度对降解效果的影响 溶液pH=6.8(不调节pH)，加入1 mL GS-nZVI悬浊液和20 mL H2O2(10%)，控制MO初始浓度分别为50，100，200 mg/L，考察了MO初始浓度对降解的影响。见图5，随MO初始浓度增大，其降解率下降。一方面可能是由于在较高的初始染料浓度下，生成的中间体竞争消耗羟基自由基所致[9]。另一方面MO分子在nZVI表面的吸附，占据了活性点位，减少了表面形成的羟基自由基[10]。

图5 不同MO初始浓度对降解效果的影响

2.2.4 H2O2的质量浓度对降解效果的影响 设定温度35 ℃，pH=6.8的条件下，在100 mL 100 mg/L MO溶液中，加入1 mL GS-nZVI悬浊液和20 mL不同质量浓度的H2O2溶液。分别考察加入5%，10%，20%，30%的H2O2对MO降解效果的影响。如图6所示，H2O2浓度为10%时，MO的降解效果最佳，反应30 min后，H2O2浓度5%和10%时对MO的降解效果趋于一致。反应中H2O2不足时，增加H2O2浓度可促进了·OH的释放，提高MO降解效率。但当H2O2过量时，如反应方程(1)，(2)所示，可能会导致·OH转化为·OOH，而·OOH的氧化能力低于·OH，使得降解效果下降[11]。nZVI+2H2O2→Fe2++2·OH+2OH-

H2O2+·OH→H2O+2·OOH

(1)

·OOH+·OH→H2O+O2

(2)

图6 H2O2的质量浓度对降解效果的影响

2.3 动力学分析

2.3.1 染料的降解动力学研究 分别采用伪一级动力学和伪二级动力学模型，模拟GS-nZVI/H2O2类芬顿体系对MO染料的降解过程。

伪一级动力学模型[12]：

(3)

式中，C0为MO初始浓度，mg/L；Ct为MO在tmin的浓度，mg/L；kobs1是一阶反应速率常数，min-1，可由ln(Ct/C0)与t作图所得直线斜率求得。

伪二级动力学模型[13]：

(4)

kobs2是二阶反应的速率常数，L/(mg·min)，以ln(1/Ct-1/C0)和t作图，可由所得直线的斜率求取。染料的两种降解动力学模型拟合结果见表1。

表1 GS-nZVI/H2O2类芬顿法降解MO的两种动力学参数

由表1可知，GS-nZVI/H2O2类芬顿法在不同温度下对MO染料的降解行为，均能采用伪一级和伪二级动力学模型进行描述。说明降解行为是氧化还原与吸附共存的过程。但根据表1中kobs1和kobs2比较可以发现吸附速率明显小于化学降解速率，因此反应以化学降解为主。随着温度从40 ℃下降到25 ℃，其降解速率从0.025 3 min-1降到0.010 7 min-1，这说明反应是一个吸热的过程。

根据阿伦尼乌斯公式[12]。

(5)

式中Ea——活化能，J/mol；

A0——指前因子，min-1；

K——伪一级吸附速率常数，min-1；

R——气体常数，8.314 J/(mol·K)；

T——反应进行的温度，K。

由lnK和1/T作图得到的直线斜率可求得降解MO染料的表观活化能Ea为45.65 kJ/mol，表明GS-nZVI/H2O2类芬顿法降解MO是表面控制的反应，具有较大的活化能(>29 kJ/mol)[14]。

2.3.2 染料的吸附动力学分析 GS-nZVI/H2O2类芬顿法降解MO包括吸附过程，因此分别采用伪一级吸附动力学模型和伪二级吸附动力学模型对吸附过程进行模拟。

伪一级吸附动力学模型[15]。

ln(qe-qt)=lnqe-k1·t

(6)

式中，qe为反应达到平衡时的吸附量，mg/g；qt为反应到tmin时的吸附量，mg/g；k1是吸附过程伪一阶反应速率常数，min-1，可根据ln(qe-qt)与t作图所得直线斜率计算得出。

伪二级吸附动力学模型[12]。

(7)

k2是吸附过程伪二级反应的速率常数，L/(mg·min)，以t/qt和t作图，由直线的斜率计算求得。两种吸附动力学模型拟合结果见表2。

表2 GS-nZVI颗粒对MO的两种吸附动力学参数

由表2可知，伪一级吸附动力学模型的r2为0.957 4～0.976，伪二级吸附动力学模型的r2为0.985 3～0.999 4。在相同条件下，伪二级吸附动力学模型的理论吸附量与实际吸附量相近。然而，伪一级动力学模型的平衡吸附实际值与理论值不同。因此，与伪一动力学模型相比，伪二级动力学模型能更好的模拟GS-nZVI对MO的吸附。因此，可以说吸附是以化学吸附为主。

为了更好地分析扩散机理，本文选取粒子内扩散方程模拟吸附过程。粒子内扩散方程如下[13]：

(8)

qt为反应到tmin时的吸附量，mg/g；KF表示粒子内扩散速率，mg/(g·min0.5)。

如图7所示，整个吸附过程中，粒子内扩散模型的变化是非线性的，这表明吸附不是一种单一的吸附方式。曲线的第一部分归因于液相扩散过程，第二部分是粒子内扩散过程。

图7 MO的吸附内粒子扩散动力学模型

2.4 吸附等温线

在35 ℃下，进行不同GS-nZVI加入量对MO降解效果试验。对数据进行等温线模拟，发现Langmuir等温线能很好地描述实验结果。Langmuir等温线方程如下[13]：

(9)

其中，qe为平衡吸附量，mg/(g·min0.5)；qm为最大吸附量，mg/(g· min0.5)；K为Langmuir常数，L/mg。所得到的参数见表3。这表明在反应中吸附阶段，MO染料与零价铁之间不直接反应，这与2.1结论相符合。吸附是单层吸附，即吸附只在吸附剂(GS-nZVI)外表面进行。

表3 在35 ℃下，Langmuir吸附等温线参数

2.5 热力学分析

通过对反应热力学行为的研究，可以确定反应过程的方向和难点。在不同的温度下进行了GS-nZVI/H2O2类芬顿体系对MO染料降解过程。反应过程的热力学参数，标准自由能变化(ΔG0)标准焓变化(ΔH0)和标准熵变化(ΔS0)，可以由以下方程得到[16]。

ΔG0=-RTlnK0

(10)

(11)

其中K0是平衡常数(K0=qe/Ce)，mL/g；热力学参数ΔG0，ΔH0和ΔS0可以从lnK0和1/T的图上确定。所得到的热力学参数见表4。

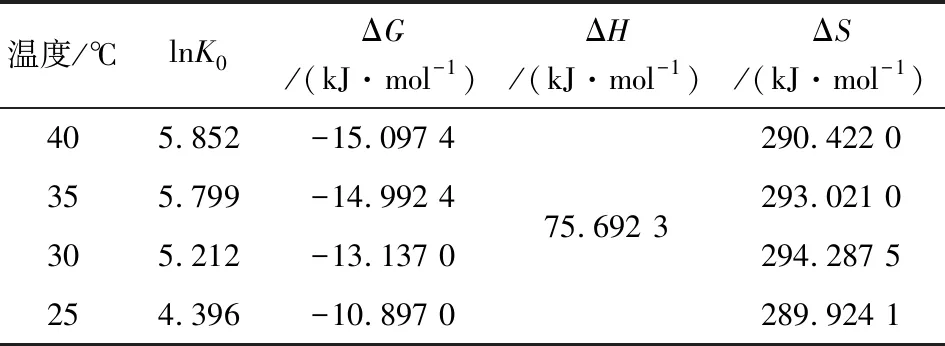
表4 GS-nZVI/H2O2类芬顿法降解MO的热力学参数

GS-nZVI/H2O类芬顿体系降解MO染料的ΔG0值均为负值，表明反应是一个自发过程。同时，ΔG0的绝对值随温度的增加而增大，这说明在较高温度下更有利于MO染料降解。标准焓变化ΔH0为正，这意味着反应为吸热过程。标准熵(ΔS0)在所有反应温度下都大于零，表明在反应过程中熵增加，熵的增加过程大于熵的减少过程，使得熵的变化是正值。结果表明，GS-nZVI/H2O2类芬顿体系降解MO染料时，溶液的无序度和自由度增加，两者的相互作用产生结构变化。

2.6 GS-nZVI/H2O2类芬顿体系对MO降解机理的研究

pH=6.8(不调节pH)，100 mL MO浓度为100 mg/L 溶液中，加入1 mL GS-nZVI悬浊液和20 mL H2O2(10%)，不同降解时间下，进行紫外-可见光全波长扫描，见图8。可见光区465 nm处，出现一个明显的吸收峰，为MO的特征吸收峰，是其偶氮特征峰；在紫外区波长范围250～300 nm间出现一个吸收峰，判断为芳香类物质的特征吸收峰[17]。随反应的进行，偶氮特征峰(465 nm)逐渐减弱直至消失，说明GS-nZVI/H2O2类芬顿试剂可以有效破解MO分子中的偶氮结构，芳香类物质特征峰强度减弱，说明GS-nZVI/H2O2类芬顿法对MO起到了降解作用。

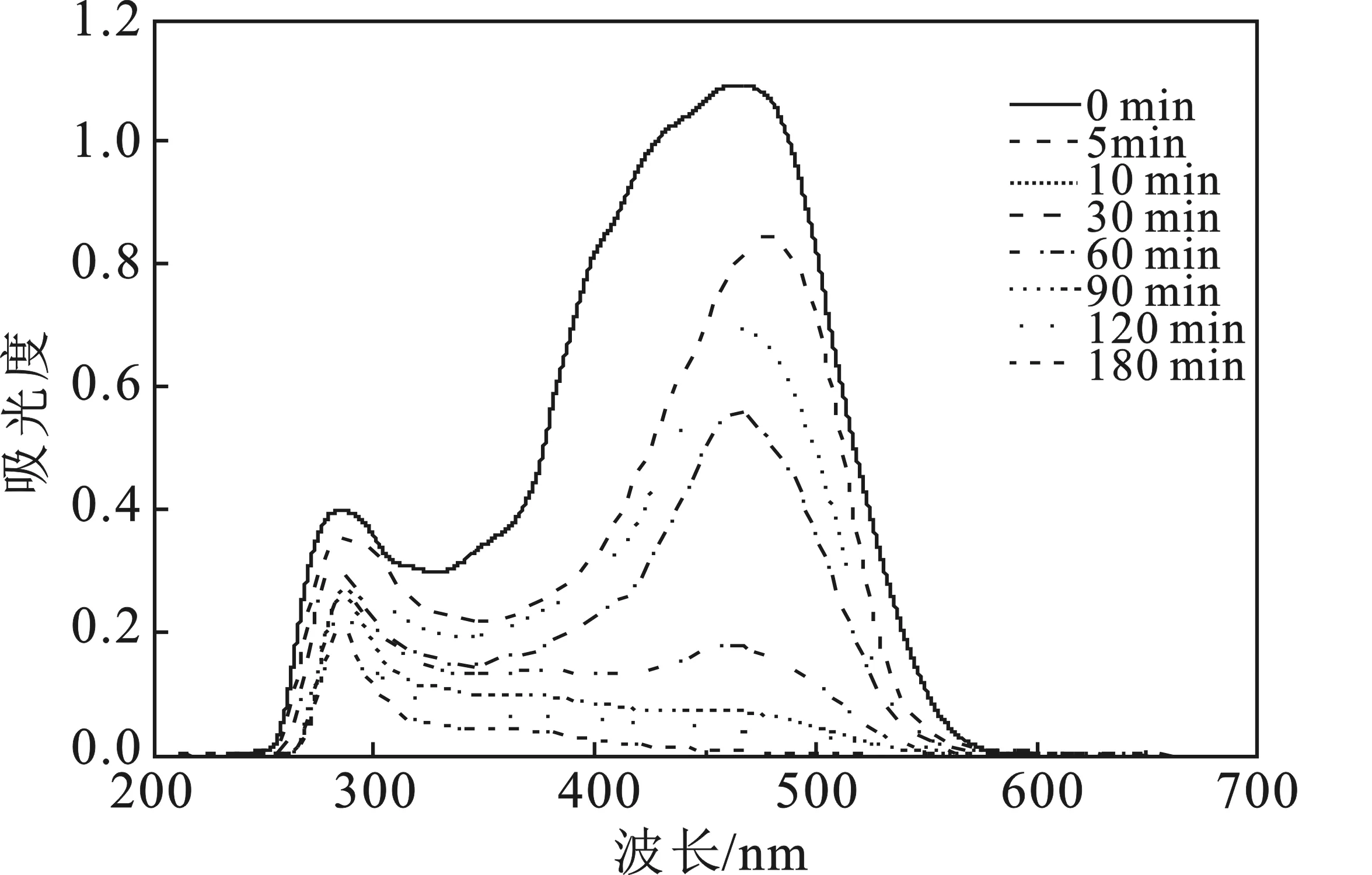
图8 降解过程中MO紫外-可见吸收光谱变化图

3 结论

(1)100 mL 100 mg/L MO溶液，pH=6.8(不调节pH)，加入1 mL GS-nZVI悬浊液，20 mL 10%H2O2，反应温度35 ℃下，反应180 min，MO的降解率可以达到97.86%。表明GS-nZVI/H2O2类芬顿法能够有效降解MO染料。

(2)溶液pH在6.8～9范围内，GS-nZVI/H2O2类芬顿法对MO染料降解效果明显优于传统芬顿法Fenton法，从而扩大了pH范围，具有重要的应用价值。

(3)拟一级动力学模型与伪二级动力学模型均能较好描述GS-nZVI/H2O2类芬顿法降解MO的行为，说明MO的降解是氧化还原反应与吸附共存的过程，降解以化学反应为主且为表面控制的反应。

(4)GS-nZVI/H2O2类芬顿法对MO的降解中的吸附过程能更好地符合伪二级吸附模型，说明该过程以化学吸附为主；粒子内扩散模型的分析结果显示：吸附不是一种单一的吸附方式，一部分归因于液相扩散过程，另一部分是粒子内扩散过程； Langmuir等温线可以描述35 ℃下的吸附过程。

(5)MO降解过程中紫外-可见全波长扫描结果显示：GS-nZVI/H2O2类芬顿试剂能够有效破解MO的偶氮结构，对MO起到降解作用。