让学生的数学探究走向纵深

杨金昌

[摘要]数学教学中，教师可通过质疑、判断、比较、分析、综合、概括等活动，引导学生经历知识产生、形成和发展的过程，使学生真正理解和掌握所学的数学知识。

[关键词]数学探究;纵深;圆锥;圆柱;体积

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2020）06-0019-01

数学课堂中，教师引导学生进行探究活动，旨在使学生通过思考习得新知，不是为了活动而活动。下面，我以《圆锥的体积》一课教学为例，谈谈如何引导学生进行开展数学探究。

案例描述：

1.引导猜想

师：请同学们猜想一下，圆锥的体积可能与什么有关系？有怎样的关系？

生1：我猜想圆锥的体积与圆柱的体积有关系，因为它们都有圆形的底面。

生2：因为圆柱的体积与它的底面积和高有关，所以我猜想圆锥的体积也与它的底面积和高有关。

2.实验验证

（1）分组实验，验证猜想。

师：请同学们拿出课前准备好的空圆锥和空圆柱比一比，你们有什么发现？（学生比较后发现圆锥与圆柱等底等高）

师：下面，我们通过实验的方法，探究等底等高的圆柱和圆锥体积之间的关系。先在空圆锥里装满沙土，然后把沙土倒入空圆柱内，看看要倒多少次沙土，才能将这个空圆柱倒满。

（2）学生以小组为单位做实验（略）。

（3）汇报交流，得出结论。

师：等底等高的情况下，圆锥和圆柱的体积之间有什么关系？

生3：圆柱的体积是与它等底等高的圆锥体积的3倍，圆锥的体积是等底等高的圆柱体积的1/3。

师：你们是怎样得出这个结论的？

生4：在空圆锥里装满沙土，然后将沙土倒入空圆柱内，正好倒了三次，将空圆柱装满，所以圆锥的体积是与它等底等高的圆柱体积的1/3。

师：根据等底等高的圆柱和圆锥体积之间的关系，可以怎样计算圆锥的体积？（师生总结出圆锥的体积计算公式）

分析与反思：

仔细分析上述教学，不难发现学生的探究过程值得反思。在实验操作中，教师直接提出用等底等高的空圆柱和空圆锥进行实验，然后要求学生将圆锥里装满沙土，倒入空圆柱里，看看倒几次后能将空圆柱装满，再根据发现推导出圆锥的体积计算公式。这里，学生虽然进行了实验，最终也得出了正确的结论，但并没有真正经历知识探究的过程，他们只是停留在简单的操作上。在这样的实验中，学生是被动进行操作的，是在教师的授意下完成实验的。同时，这样教学也暴露出教师在设计实验帮助学生进一步探究方面的不足。那么，该如何改进教学呢？如何提高学生探究的有效性呢？这是教师不得不思考的问题。

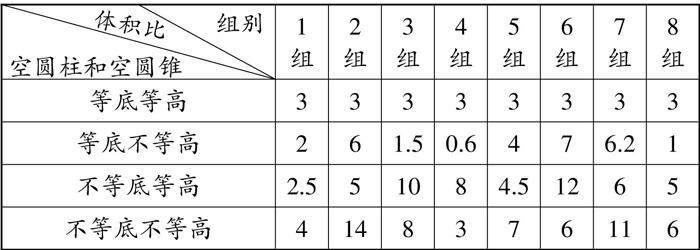
为了让学生真正理解等底等高的圆锥和圆柱体积之间的关系，我在原来的基础上增加了等底不等高、等高不等底以及不等高不等底这三组圆柱和圆锥的体积比较。如下图所示：

通过观察、對比，学生容易得出“圆锥体积等于等底等高的圆柱体积的1/3”这一结论。在随后的公式运用中，很少有学生会忘记网锥的体积计算要乘以1/3。在此基础上，我利用表格中的数据引导学生进一步思考：“圆锥的体积是圆柱体积的1/3，那么，圆锥和圆柱一定等底等高吗？”通过问题，使学生更深刻地理解了圆锥和圆柱体积之间的关系。

总之，数学教学中，教师可通过质疑、判断、比较、分析等活动，引导学生经历知识产生、形成和发展的过程，使学生真正理解和掌握所学的数学知识。

（责编 杜华）