斑马线“人-车”博弈仿真*

段在鹏 黄月铃 王秀萍 黄萍 沈斐敏

(福州大学环境与资源学院 福州 350116)

0 引言

2017年6月公安部交管局发布数据，近3年来，全国共在斑马线上发生机动车与行人的交通事故1.4万起，造成3 898人死亡，其中机动车未按规定让行导致的事故占总数的90%[1]。同年10月1日起，驾考新规规定驾驶员应主动避让优先车辆和行人，全国各地也广泛开展机动车不礼让行人等交通违法专项整治[2]。经过警民共同努力，斑马线乱象治理效果显著[3]。如据西安市统计局发布结果，83.0%的受访市民认为“车让人”行动以来西安市的交通秩序有好转[4]。杭州市区道路斑马线前机动车的礼让率已超过93.91%，公交车“礼让斑马线”率达到99%[5]。斑马线事故得到有效控制，但其是否影响到了交通安全的整体态势？

本文汇总学者李生才等首次统计的2016年5月[6]至2018年6月[7](该时间区间包含但不止于“车让人”活动区间)交通事故数据见图1。由图发现，2年来交通事故总量及所占总事故比率均未发生明显变化，虽在2018年1月至4月出现了短暂下滑，但之后又开始回升。即“车让人”虽然有效控制了斑马线事故，但对总的交通事故控制并未产生明显影响。

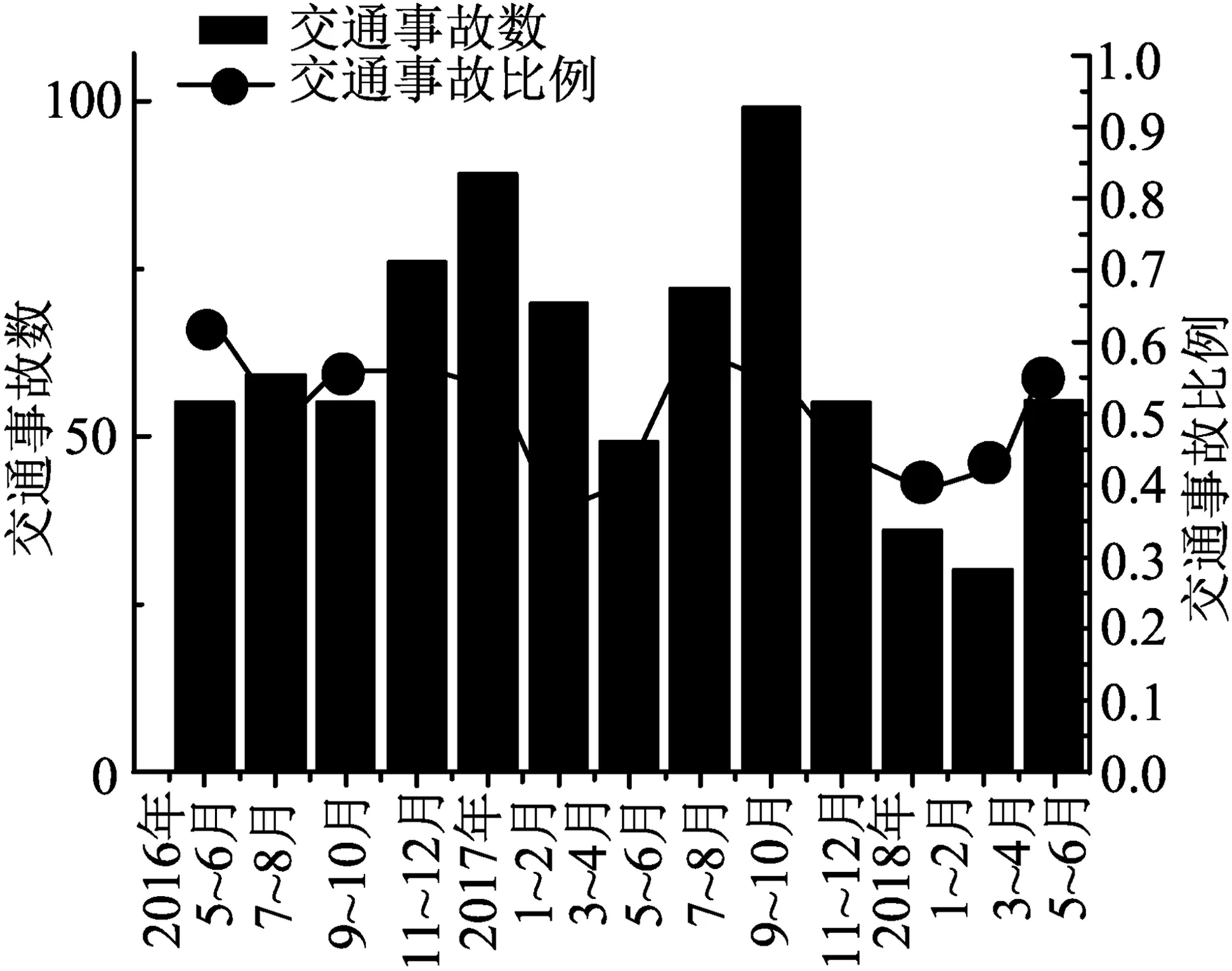
图1 2016年5月—2018年6月国内交通事故数及占比统计

是什么原因使“车让人”对整体交通安全态势失去影响？国内在此方面的研究很少，基于此，本文通过斑马线“人-车”博弈仿真，分析原因。

1 无规定“车让人”情况下的“人-车”博弈

“车让人”实际上是司机与行人经过博弈之后，做出能使双方利益最大化的选择。

博弈论作为一种决策理论，它可以模拟利益冲突的不同利益相关者间的交互[8]，它通过对人们相互之间存在互动关系、策略对抗情况下的决策选择，为个人或组织的正确决策提供指导[9]。2017年，Bjornskau T[10]的研究结果首次明确表明，博弈论建模是理解道路用户交互行为的有效工具。本文在以下两种不同背景情况下，将司机和行人的选择进行博弈。两种不同背景情况如下。

(1)仅考虑司机与行人能获得的实际利益(外在利益)与心理感受(内在利益)。

(2)规定机动车必须礼让行人，否则扣分或罚款，同时考虑司机与行人能获得的实际利益(外在利益)与心理感受(内在利益)。

2012年，梅强等[11]设计调查问卷对员工生命价值进行评估，开创性地发现员工的生命价值评估值呈正态分布，而周涛等[12]提到的泊松分布被广泛用来表示人的行为活动。故而本文中行人和司机的外在利益可以用正态分布表示，内在利益可以用泊松分布表示，之后本文组织15人分别对3种典型场景情况，进行了150次实验。实验按人员伤害、财物损失、时间、心态等，规定收益值在[-10,10]之间，根据不同的情况选取。整理实验数据后，分别确定正态分布(外在利益)和泊松分布(内在利益)的分布参数。该第一种背景下的司机和行人收益分布如表1所示。

以表1中N(-2,1)+P(1)为例，表示当行人和司机都行动时，行人的收益分布。其中，N(-2,1)表示行人获得的外在利益服从一个数学期望为-2、标准差为1的正态分布，P(1)表示行人获得的内在利益服从数学期望和方差均为1的泊松分布。

表1 无规定“车让人”情况下司机与行人的收益分布

注：N(μ，σ)表示正态分布，P(λ)表示泊松分布。

利用matlab对50对司机与行人的行为进行博弈仿真，统计仿真得到的50个纳什均衡点，并用图表示，观察纳什均衡点的分布。50对行人与司机的行为博弈产生的收益统计如图2所示，纳什均衡点分布如图3所示。

图2 无规定“车让人”情况下的最优方案中行人与司机收益统计分布

图3 无规定“车让人”情况下的最优方案分布

图3的4个方格与收益矩阵方案一一对应。方案一：行人、司机均行动，对应图3的标号①；方案二：行人行动、司机等待，对应图3的标号②；方案三：行人等待、司机行动，对应图3的标号③；方案四：行人、司机均等待，对应图3的标号④。由图可知，50次博弈产生的纳什均衡点大部分集中在方案三的框中，在没有规定“车让人”时，只有约五分之一的司机选择礼让行人。

需注意的是博弈仿真所得结果为司机的“积极礼让率”。积极礼让表示司机从内心愿意礼让行人，而真实礼让则表示受限于现实情况，司机实际的做法。从图3可以看出，司机的积极礼让率为20%。

2 规定“车让人”情况下的“人-车”博弈

2.1 “人-车”博弈

在规定机动车必须礼让行人，否则扣分或罚款，同时考虑司机与行人能获得的实际利益(外在利益)与心理感受(内在利益)的背景下，利用根据实验既已确定的正态分布和泊松分布，随机抽取司机和行人所获得的收益，具体如表2所示。

表2 规定“车让人”情况下司机与行人的收益分布

注：N(μ，σ)表示正态分布，P(λ)表示泊松分布。

以表2中N(-2,2)+P(1)+N(-3,1)为例，表示当行人、司机都行动时，司机的收益分布。其中，N(-3,1)表示由于司机没有礼让行人，得到的利益服从数学期望为-3、标准差为1的正态分布。在第二种背景下，50对行人与司机的行为博弈产生的收益统计如图4所示，纳什均衡点分布如图5所示。

图4 规定“车让人”情况下的最优方案中行人与司机收益统计分布

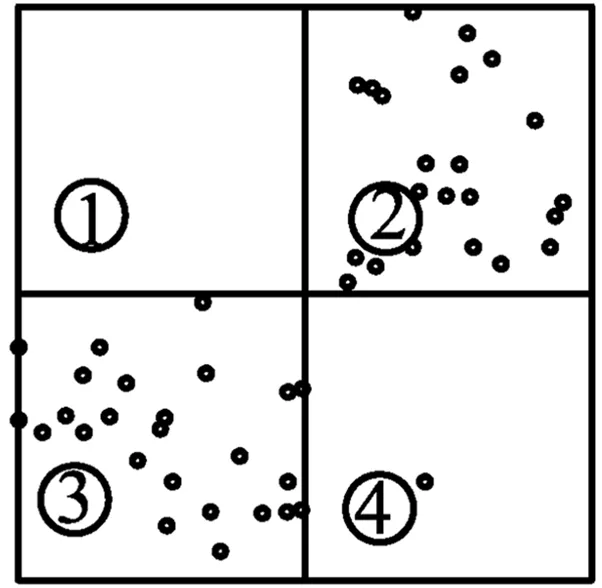
图5 规定“车让人”情况下的最优方案分布

图5的4个方格与收益矩阵方案一一对应。从图5可以看出，在规定司机必须礼让行人的情况下，博弈后有一半的司机选择礼让行人，一半的博弈结果是选择方案三：人等车行。

虽然规定了“车让人”后，博弈产生的纳什均衡点也更多地落在“车让人”的方案上，但由于一旦发生事故，行人受到的伤害更大，因此，博弈结果仍有一半选择“人等车”。另一方面，在车让人过程中，还隐藏着危险——潜藏在礼让司机的心里的危险。

经收集相关信息[2,4,13]，发现礼让司机的不满主要集中在两点：其一，礼让时间太久从而变得焦躁；其二，礼让后，行人散漫的态度让司机心生不满。阿根廷学者Escanés G等[14]通过实验得出：进度阻碍、敌对姿态、侵权行为是引起路怒的主要因素。本文总结的礼让时间太久可隶属于“进度阻碍”，行人态度散漫则可隶属于“敌对姿态”。故而这两种负面情绪共同指向了近年耳熟能详的交通危险源——路怒(road rage[15])。

据统计，我国35%司机承认属于“路怒族”[16]，而我国超过10%的交通事故起因都是“路怒症”[13]。例如，司机可能因礼让时间过久，驶离斑马线区域后便超速驾驶，而后与前车追尾；也可能因为“散漫行人”的影响，情绪变得糟糕，驶离斑马线后，骑线驾驶而与临车刮擦。

综上可推得：如果没有很好地兼顾司机情绪，“车让人”并不能实现本质安全。此时，事故总量并无很大变化，只是事故地点变了，从斑马线推移到了公路的其他地方(事故外溢)。

综上所述，可以得出以下要点：

(1) “车让人”是正确的，因为它瞄准的是“占全国交通事故90%的机动车未按规定让行事故”。

(2)接下来的任务重点是：在控制让行事故的同时，防止事故“外溢”到道路的其他区域。

(3)控制的重点。车拥有坚硬的钢铁外壳和人望尘莫及的速度，而行人是血肉之躯，所以司机是主动方，故而车让人过程的控制重点是司机。

2.2 司机心境分析

司机心境包含积极和消极等两种极端心情。正常驾驶过程中，司机心情处于积极与消极之间，即为平常心，如图6。在礼让行人过程中，随着礼让时间不断增长，或者当看到散漫的行人，司机心情由积极过度为消极，如图7，情况越恶劣，心情便会沿图7中的a线迅速地转变为消极，最终造成路怒。路怒是应避免的，因为路怒会造成事故的“外溢”。

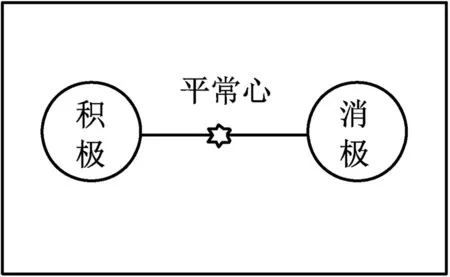
图6 司机平常心状态下的心境

3 加入正向反馈下的“人-车”博弈

3.1 构建“人-车”正向反馈回路

据以上调研可知：“礼让时间过长”和“散漫的行人”都是客观存在的，故而a线无法删除。为缓和司机心境，便只剩一种方法：即从消极心情再引出一条b线返回积极心情，从而构成图8的反馈回路。图8表示：不否认积极向消极的变化(a线)，即承认礼让时间增长和个别散漫行人对司机的消极影响，但也可以在司机心中架起一道桥(b线)，让消极变为积极。在a线与b线的交互下，司机整体的心境被中和，路怒也被消除。

图7 司机礼让状态下的心境

图8 出现反馈回路的司机心境

法国学者Guéguen N等[17]在他的文章《论行人微笑和司机行为的关系》中总结：行人一笑，驾车者就放慢了车速。故而本文认为b线应主要由行人来搭建。b线的正确搭建方式，即：只要行人给司机一个正向的鼓励(微笑、点赞)。

3.2 正向反馈后的“人-车”博弈

此时，“人-车”博弈的背景变为：规定机动车必须礼让行人，否则扣分或罚款，并且，当司机礼让行人时，行人要对司机回以感谢，同时考虑司机与行人能获得的实际利益(外在利益)与心理感受(内在利益)。在这个背景下，利用根据实验既已确定的正态分布，随机抽取司机和行人所获得的收益，具体如表3所示。

表3 正向反馈后的司机与行人的收益分布

注：N(μ，σ)表示正态分布，P(λ)表示泊松分布。

以表3中N(2,1)+P(0.1)+N(2,2)为例，表示当行人行动、司机等待时，司机的收益分布。其中，N(2,2)表示司机礼让行人，得到的收益服从数学期望为2、标准差为2的正态分布。在这个背景下，50对行人与司机的行为博弈产生的收益统计如图9所示，纳什均衡点分布如图10所示。

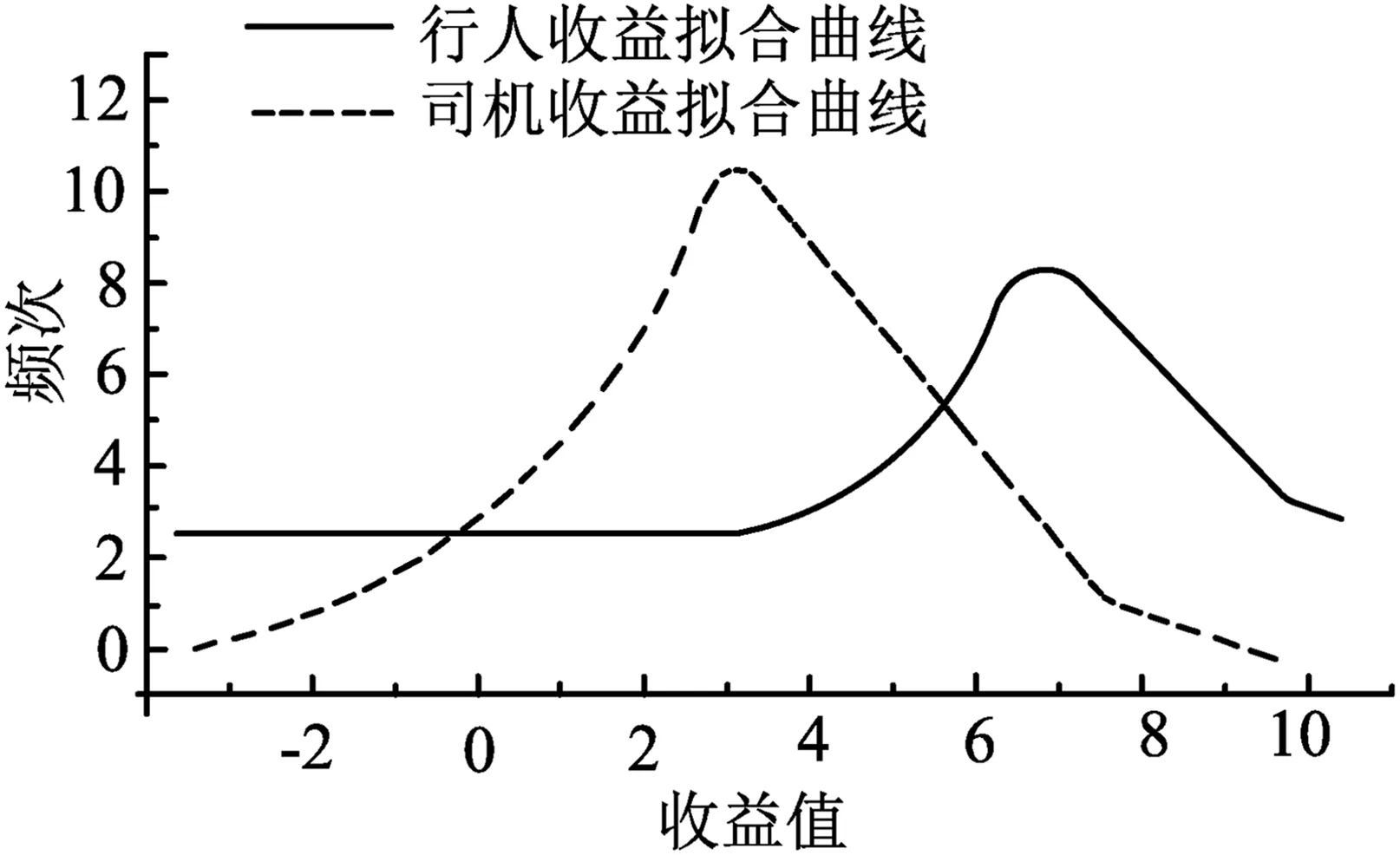
图9 加入正向反馈下的最优方案中行人与司机收益统计分布

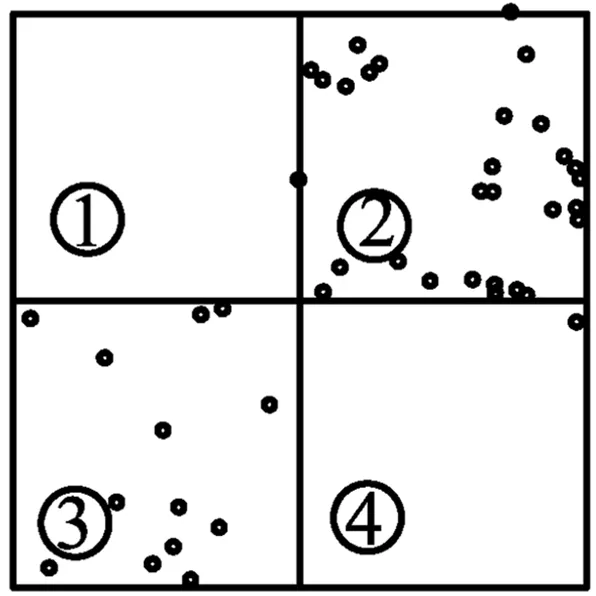
图10 加入正向反馈下的最优方案分布

图10的4个方格与收益矩阵方案一一对应。从图10可以看出，在规定司机必须礼让行人，并且行人对司机的礼让行为表示感谢的情况下，博弈后有70%左右的纳什均衡点落在方案二的框图中，表示有约70%的司机选择礼让行人。可以看出，在司机收到正向反馈后，选择“车让人”的司机数增加。

4 改善措施

基于以上分析，本文建议在斑马线位置设立司机和行人阅读的两套标语，综合防控“斑马线事故外溢”。即：分别用司机阅读的标语减弱a线影响，而用行人阅读的标语强壮b线影响。双管齐下，综合调控司机心境。张海英[18]探讨了鞠躬致谢的弊端，故而本文也不建议使用较为耗时的正向动作，应多推荐微笑、点赞等简易动作。本文给出了两套方案如表4。

表4 司机与行人阅读的两套标语方案

通过分析，发现方案一更官方化，它以交管部门的语气来传达讯息，此时司机和行人都是处于被动位来接受信息；而方案二，交管部门则置身善意提醒者的位置，此时司机和行人处于主动位，可以充分以局中人的身份来减弱a线或者强壮b线，从而使得信息更好地被接收。通过调研，方案二的讯息接受效率也会更高。综上，本文建议在斑马线位置推广第二套方案。

5 结论

(1)现阶段“车让人”可有效控制斑马线事故，但对交通安全整体态势影响较小。通过博弈仿真，结果发现在没有规定“车让人”时，司机的积极礼让率为20%。

(2)“车让人”事故外溢。虽然通过博弈仿真发现，规定车让人能提高礼让率，司机的积极礼让率约50%，但是如果没有很好地兼顾司机情绪，“车让人”并不能实现本质安全。即此时，事故总量并无很大变化，只是事故地点变了，从斑马线推移到了公路的其他地方。

(3)司机心境分析与控制。文章将司机心境分为积极和消极两种心态，“礼让时间过长”和“个别散漫行人”会使司机心境由平和转向消极，但可以在司机心中构建“消极→积极”关系，以中和司机整体的心境。“消极→积极”关系应由行人主导构建。通过博弈仿真发现，司机收到正向反馈时，司机的积极礼让率约70%。另一方面，为保证路口的通过速度及人身安全，本文不建议使用耗时的正向动作，推荐微笑、点赞等简易动作。

(4)改善措施。文章建议在斑马线处分别设计给司机和行人阅读的两套标语，司机阅读的标语可减弱“积极→消极”影响，行人阅读的标语可强壮“消极→积极”影响，双管齐下，综合调控司机心境，防止“斑马线事故外溢”。