我国不同股票指数的风险及绩效评估

范高乐

（1.天津天狮学院经济金融学院，天津301799；2.河北工业大学经济管理学院，天津300401）

一、前言

我国建立股票市场的时间为1990年11月26日，其主要标志是上海证券交易市场的成立，同年的12月1日建立了深圳证券交易所。在三十年的发展过程中，我国股票市场既经历过“8∙18申能保卫战”这样的惨烈熊市，也经历过2007年的历史性牛市。也出现很多对我国股票市场造成巨大冲击的重要事件，最典型的是2015年的“股灾”，创业板指数从年初的1472.345点暴涨到2015年6月3日的3982.25点，上证综指从年初的3234点暴涨60%，6月12日达到历史最高点5178点，而在6月15日星期一“股灾”开始之后，上证综指最低点暴跌到2850.71点，深证成指更是从“股灾”前的18212点大跌50%到9259.65点。从历史数据来看，我国股票市场的波动是十分剧烈的，具体到不同的股票交易市场，波动的剧烈程度及特征也各有特点。之所以选择上证综指、深证成指、中小板指、创业板指等四个股指数据，是因为股指数据充分反映了该市场上股票价格的总体水平及其变动状况。通过实证研究四个股票交易市场的股指数据，能够分析得到各自的风险特征。通过引入绩效评估指标夏普比率，可以比较不同交易市场的投资效率。文中的实证研究结果可以为政府更加有效地监管市场提供建议，也能够帮助市场投资者更为理性地参与市场交易。

二、国内外文献综述

国外的大量实证研究说明，利用GARCH 族模型能够真实呈现金融市场存在的变化特点。Glosten，Jagannathan和Runkel（1993）就是在这个模型的基础上，描述了差异化模型条件方差影响股市收益的情况。研究结果说明，该模型可对收益率产生的变化集聚性进行呈现。Bollerslev 和Hans（1996）通过蒙特卡罗提出的模拟方式，基于金融市场形成的波动率研究了GARCH和EGARCH模型，并发挥了拟合作用，对于美国的股市波动率来讲，该模型具有良好的拟合精度。Andersen 和Bollerslev（2000）研究了日本东京股市产生的集聚变化特性，以及随之产生的长记忆特性。

我国相关研究人员针对四个股票指数的波动特点开展了一系列的研究。其中王晓芳、王瑞君（2012）采取EEMD全面分析了三个分量，分别为高频、低频分量和趋势项目，从而综合借助VaR模型真实解析了上证综指的波动情况，并对有关参数干扰收益率的情况进行了分析。杨科、陈浪南（2013）在全面掌握中国股市波动特点的前提下，建立了一个非对称、可以自适应的HAR-D-FIGARCH 模型，并经过全面验证对中国股市的精确度进行判断。任继勤、单晓彤、梁策（2015）采取GARCH 模型与VaR方法共同联系的方式对中国主板和创业板市场风险合理评价，并通过曼-惠特尼U 验证方法统一对比两者，研究结果说明，中国主板和创业板存在相当显著的ARCH效应，收益率明显，其中还具备较强的稳定性、非正态性和尖峰后尾等特征，同时创业板市场存在的风险显著超过了主板市场的风险。因此，文中将通过建立合适的GARCH 模型，并且在度量风险时引入夏普比率的方式，比较四个股指风险波动特征的区别。

三、基于GARCH模型的股票指数的波动性研究

文章运用GARCH 模型分别对四个股指日收盘价的对数收益率序列进行参数估计，进一步分析四个股指样本的对数收益率时间序列的风险特征。需要重视的是，在建模的过程中，GARCH 模型将平稳性作为主要特点，只有保持稳定的序列，才可以通过GARCH模型实施建模，因此稳定性判断是GARCH模型设计的前提。

1.数据来源

选取上证综指、深证成指、中小板指以及创业板指当日收盘价作为实证分析样本，选取样本主要考虑以下两点：一是创业板是从2010年6月1日开始公布每日收盘价，二是选取时间要足够长，这样有充足的历史数据，更有利于文中的统计分析。因此文中的样本区间选定在2010 年6 月1 日至2017 年12月31日，一共1845个交易日。全部数据来源于同花顺iFinD数据库，所有的实证分析基于Eviews8.0软件和Excel软件完成。

分析了对数收益率的对象，也就是当天的收盘价格。Rt的主要作用是对第t日的综合收益率精准标记，围绕Rt产生的表达式：

其中，Pt为相应资本市场第t 日的收盘价，Rt（t=1，2，3，4）分别是指上证综指、深证成指、中小板指、创业板指每日收盘价的对数收益率。

2.模型检验

（1）平稳性检验

验证稳定性可以选择两种方法：ADF（Augmented Dickey-Fuller）检验和DF 检验。当开展ADF 验证时，综合思考以下问题：

①回归定义合理的滞后阶数，通常采用AIC准则来确定给定时间序列模型的滞后阶数，即AIC准则更小的模型拟合效果更好。

②如果验证与原假设发生冲突，序列不会出现单位根，属于稳定的序列，反之则说明该序列不够稳定，还要深刻验证差分，直到对原来的假定拒绝，从而掌握与序列对应的单整阶数。

文中采用ADF检验对四个股指的日对数收益率序列进行平稳性检验，结果如表1所示：

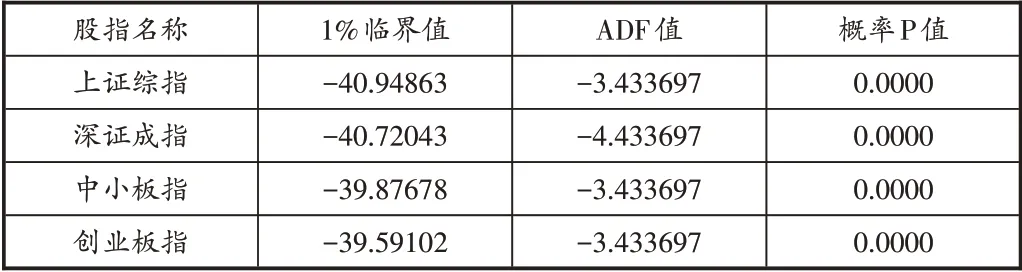
表1 ADF检验结果

由表1可知，四个股指形成的统计ADF量值都明显低于临界值1%，因此要对原假设拒绝，即没有单位根，可以说明四个股指日收盘价的对数收益率序列表现出稳定性。

（2）自相关检验和异方差检验

表2 股指日对数收益率ARMA模型

针对样本的时间序列实行严格验证，结果表明，Q统计量十分显著，且自相关系数（AC）和偏自相关系数（PAC）均明显不为0，可见序列明显具有自相关性，且自相关图和偏自相关的系数明显具有拖尾特征，进行滞后回归估计时应选用自回归移动平均模型（即ARMA模型），从而确定均值方程。同理，经检验结果可知，深证成指、中小板指、创业板指的日对数收益率序列同样明显具有自相关性，且自相关系数和偏自相关系数具有明显的拖尾特征，因此选用自回归移动平均ARMA模型进行滞后回归估计，确定最优滞后阶数。经过反复持续的检验通过四个股指初步评价收益率序列，从而建立模型得出结果。

对均值方程得出的残值序列严格验证，决定采取ARCHLM方法检查异方差性具有的隐蔽性，还可以称为ARCH 效应验证。通过Eviews8.0 软件的操作得到检验结果，可以看到四个股指日对数收益率序列在选定的ARMA模型下，伴随概率值均小于5%，具有显著的ARCH效应。以上证综指为例，F统计量为103.0399，伴随概率值为0.0000，故拒绝原假设（原假设为残差序列不存在ARCH 效应），所以上证综指的每日收盘价的对数收益率存在ARCH效应，需要采用GARCH模型来对方差序列进行建模。

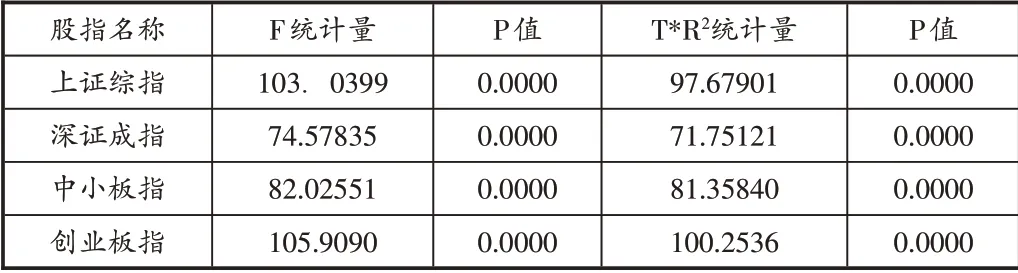
表3 ARCH效应检验

3.基于GARCH模型的股指波动性研究

（1）基于GARCH模型的深证成指的波动性研究

根据前文的说明，深证成指的对数收益率时间序列R2是平稳序列，且存在着异方差现象，这两点满足了建立GARCH模型的前提，因此，文中建立GARCH 模型以进行进一步的研究。与GARCH 模型相关的方程有两个：一是与ARMA(p，q)模型具有高度一致性的均值方程，通过下式进行描述：

此时深证成指的均值方程为：

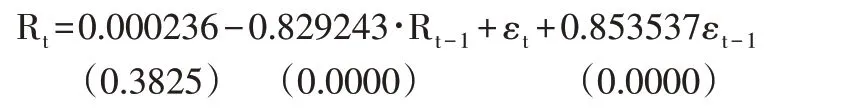
第二行为均值方程各系数的伴随概率值。

另一个是方差方程。方差方程的表达形式为：

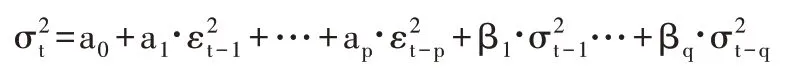
其中，a0＞0，ai≥0，βi≥0，i=1，2，…p（或q）

需要引起重视的是，对GARCH 模型积极假设，并使残差形成三种分布。在具体研究过程中，围绕误差项开展不同程度的假设分布验证，从而得到最理想的模型。通过上述统计性结果描述可知，四个样本序列都与正态分布不相符，可假设残差序列满足GED分布和t分布的要求，得出残差分布不同假设带来的GARCH模型。表4是在GED分布下几个典型的GARCH模型，C（n）从左往右代表方程中的系数项，n=4，5，6，7，8。

GARCH(1，1)模型包含的两个系数ARCH项和GARCH项，在置信水平不超过95%时满足显著性检验要求，其他模型及系数都与检验不符。虽然均值方程的常数项无明显特点，但也可以不考虑常数项带来的不良干扰。因此，根据GED分布特点，模拟后具有最高拟合度的是GARCH(1，1)。在t 分布下，同样是只有GARCH(1，1)模型的ARCH 项系数和GARCH 项系数在95%的置信水平下是显著的，具体过程这里不再赘述。将GARCH(1，1)置于两种分布假设下，对比AIC值可知，该值在t分布下为-5.678895，基于GED 的分布，得出-5.681235，根据AIC 信息原则得知，AIC 不断降低数值，相应获得更优的模拟值①Akaike information criterion,AIC信息准则，是衡量统计模型拟合优良性的一种标准。。实证检验说明，根据GED形成分布，利用GARCH(1，1)模型可以形成最佳的拟合度。

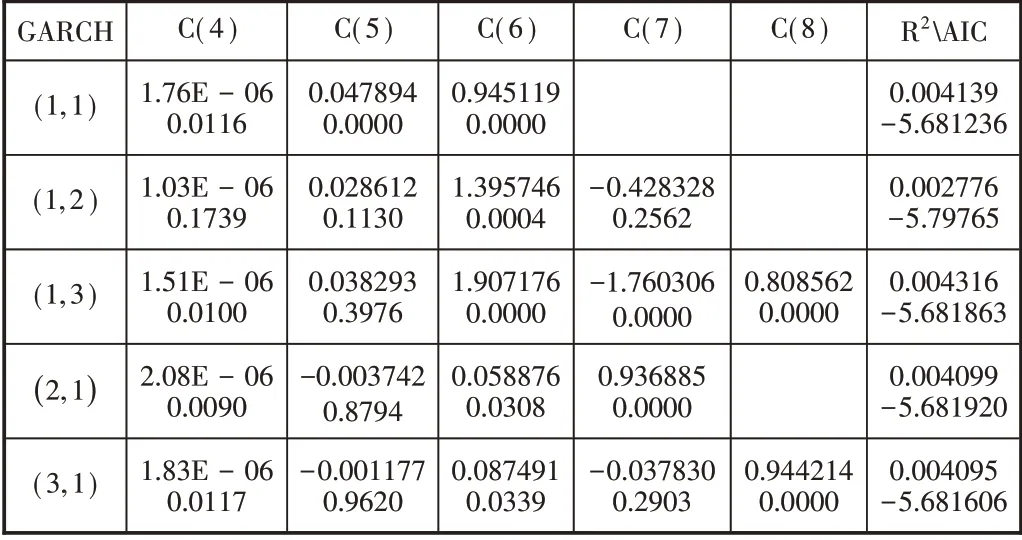
表4 GARCH(p，q)模型的参数估计比较

由表4参数估计结果可知，深证成指的GARCH(1，1)模型的方差方程确定为：

第二行为方差方程各系数的伴随概率值。

由方程可知，ARCH 和GARCH 分别产生了0.047894 和0.945119 的系数，二者都不超过1，与方差稳定约束的标准相符。由于两个系数之和显著等于1，说明深证成指呈集聚性的波动。结合之前的研究表明，全部尖峰厚度特征的时间序列特点为：随机干扰项产生了常数的无条件方差，且不具有固定特点，我们可以对之前深证成指存在的尖峰后尾特点进行明确分析。由于ARCH项和GARCH项产生了与0非常近似的P值，二者都符合显著检验的标准。之后科学验证GARCH(1，1)模型产生的残差数值，决定由此产生的异方差效应是否真正清除，结果如图6，利用F相关性验证产生对应的统计数据1.510819，P值是0.2177。有效对应了原假设的结果，代表残差序列难以形成ARCH 效应。通过Eviews8.0 软件的操作，文中在建立完成GARCH(1，1)模型后，生成了GARCH(1，1)模型方差序列G2，G2的基本数字特征的均值为0.000270。

（2）基于GARCH模型的中小板指数的波动性研究

采取类似于深证成指的方法，对中小板指日对出收益率时间序列构建GARCH 模型。实证结果说明，当GARCH(1，1)模型具有的置信水平达到95%时，由此形成显著系数的均值与方差方程。假定残差形成t 分布与GED 分布，前者的AIC 值对应分布数据-5.604833，后者的AIC 值对应分布数据-5.598249。因此，结合t 分布的具体特征，GARCH(1，1)产生极高的拟合度。

通过下式明确中小板指的平均数值：

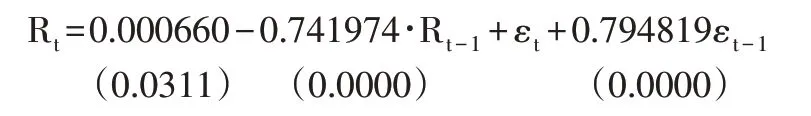
第二行为均值方程的各系数的伴随概率值。

中小板指的GARCH(1，1)模型的方差方程确定为：

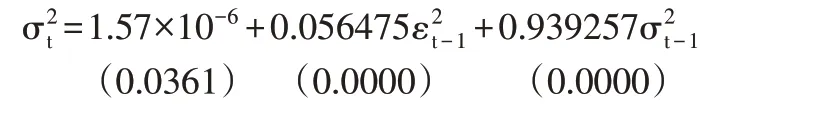
第二行为方差方程的各系数的伴随概率值。

通过方程分析可知，方差方程将ARCH项系数和GARCH项系数作为评估稳定性的重要准则。由上文对深证成指波动聚集性的分析过程可知，中小板指数的波动同样具有集聚性的特征。并初步得到检验中小板指GARCH(1，1)模型的最终结果。不少数据表明，通过F 验证可以对量值有效统计，得到0.790705，基本概率0.3740，基本符合原来假设的结果，序列难以产生ARCH效应。

通过Eviews8.0软件的操作，文中在建立完成GARCH(1，1)模型后，生成了中小板指GARCH 模型的方差序列G3，均值为0.000291。

（3）基于GARCH模型的创业板指数的波动性研究

建立创业板指日对数收益率时间序列的GARCH 模型与上文采用的方法类似。实证结果说明，假定通过t分布和GED分布对残差有效处置，AIC 通过t 分布得到真实数据-5.200856，在GED分布下AIC的实际数值-5.196276，因此，GARCH(1，1)在t 分布下形成最高拟合度，当置信水平不超过95%时，方差方程的ARCH项系数和GARCH项系数呈全部显著性。

此时，创业板指的均值方程确定为：

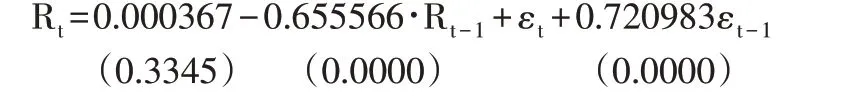
建立创业板指GARCH(1，1)模型的方差方程为：

由方程了解到，上述两个系数都符合条件方差方程的稳定性要求，并且由方差方程可知，创业板指体现出集聚性波动。ARCH-LM 检验的结果显示，F 检验的统计量值为0.151309，概率值为0.6973，所以接受原假设，该序列已经消除了ARCH效应。

通过Eviews8.0软件的操作，文中在建立完成GARCH(1，1)模型后，生成了中小板指的GARCH方差序列G4，G4的均值为0.000425。

（4）基于GARCH模型的上证综指的波动性研究

根据之前研究的方法对上证综指对数收益率时间序列构建对应的数学模型。实证结果说明，该模型的AIC 数值在t 分布的情况下得出-6.151109，在GED 分布的情况下AIC 数值具体为-6.14508。因此，经过t 分布模型产生的拟合度必将最高，保证置信水平达到95%时，均值方程和方差方程产生的ARCH项系数和GARCH 项系数形成了明显的特征。此时，创业板指的均值方程确定为：

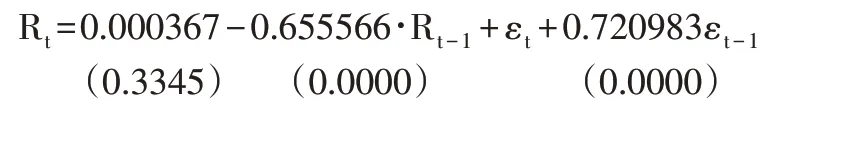
建立上证综指GARCH(1，1)模型的方差方程为：

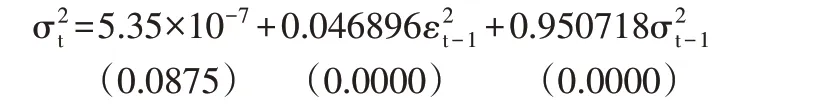
由以上方程了解到，两个系数都符合条件方差稳定性要求，同时由方差方程可知，上证综指表现出集聚性的波动。对上证综指采取ARCH-LM 检验以后，得出统计量的实际结果0.660193，与之相应产生的概率值为0.4166，这个结果原假设的设定，初步确定这一序列难以产生ARCH 效应。通过Eviews8.0软件的操作，文中在建立完成GARCH(1，1)模型后，生成了上证综指的GARCH方差序列G1，G1的均值为0.000198。

4.股票指数的绩效评估

（1）夏普比率的数据来源

由前面的夏普比率介绍部分可知，假设存在无风险利率rf时，夏普比率Sp的表达式为：

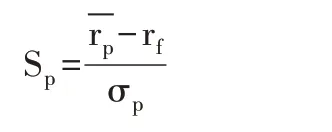
上证综指、深证成指、中小板指、创业板指等股指每日收盘价对数收益率系列产生的收益率平均数值可以通过-rp(p=1，2，3，4)表示。rf代表风险得到的基本收益率，由于实际市场不会产生风险利率，故可以初步判断这一风险利益是0。标准差σp来源于四个股指日对数收益率时间序列的GARCH(1，1)模型所生成的方差序列均值作为σ2

p。

（2）夏普比率的计算与分析

夏普比率表达式确定为：

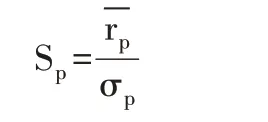
计算可得四个股票市场的夏普比率，如表5所示：

表5 夏普比率

在引入了夏普比率后，文中进行了四个市场投资效率差别的比较，从市场因素和人为因素两个角度解释四个股票交易市场之间的波动差异和投资效率差别。首先，创业板和中小板的波动较之沪深A股市场明显更为剧烈，投资的性价比却又明显更高，创业板市场的服务对象主要是在短期内不能在主板上市出现的具有创业特点与高科技特点的企业，与主板市场比较其准入门槛不高。这些特性直接决定了在经营业绩方面，创业板上市企业容易出现更加强烈的模糊性。当面对风险时，创业板上市企业被宏观经济与国家政策变化因素干扰的可能更大。其次，创业板市场拥有很多散户投资者，这部分投资对象容易引发投资过度的现象，无形中增加了市场的风险概率。

四、结论

经过系统分析四个股指样本的变化特点可知，其对数收益率时间序列的波动变化异常强烈。分析四个样本的基本统计特征还可以得到，标准差从小到大依次是上证综指、深证成指、中小板指、创业板指，最小的上证综指标准差为0.013974，最大的创业板指标准差为0.020513。因此，创业板指的波动幅度最大，而上证综指的波动幅度最小，且四大股指均具有波动集聚性、非正态分布、尖峰厚尾的特征，因此，在建立GARCH模型时就需要考虑t分布和GED分布两种分布情况，并且依据AIC准则确定更为合适的分布条件。从ARCH效应的角度来看，四个股指日对数收益率时间序列均具有明显的ARCH效应，呈现集聚波动特点，即大波动彼此相连，小波动持续不间断出现，客观说明主板市场、创业板市场以及中小板市场不具备有效性。就目前的中国股票市场而言，GARCH 模型能较好地反映出股票指数的波动集聚性，并且具有相对较好的拟合精度。通过持续强化模型的应用效率，为进入市场者提供一些准确的预测信息。绩效评价研究中，文中比较了四个股指的夏普比率的大小，创业板和中小板的投资效率明显高于沪深主板市场，但是创业板和中小板的波动幅度也要高于沪深主板市场。