n阶方阵高次幂的求解方法

张海涛

（山西大同大学数学与统计学院，山西大同037009）

在线性代数中，矩阵是主要的研究对象之一，其中方阵的幂是矩阵乘法的一种特殊情况[1-3]。求解方阵幂的过程中会用到归纳、拆分、相似矩阵等多种方法和技巧，给出六种常见的求解方法。

1 直接计算法

基本思路:依次计算A2,A3, …, 找出它们的规律,猜想An,然后用数学归纳法证明即可。

运用这个方法一般都是先计算。

A2,A3, …，并根据A2,A3…的计算结果进行猜想，而后对猜想用数学归纳法加以证明,但并不是所有矩阵的幂的元素跟幂指数都有较明显的关系，故此方法有一定的局限性。

2 利用二项展开式

若方阵A能分解成两个两个方阵的和A＝B+C,且BC=CB，则可用二项式展开定理An=(B+C)n=当然要求B,C之中有一个的幂都很容易计算，特别地，当A的主对角线上的元素相同时,利用二项式计算更为方便。

例2计算

解记注意到A的主对角线上元素均相同,于是A=B++λE, 其中易知Bk=0(k≥2),故A50=(B+λE)50=

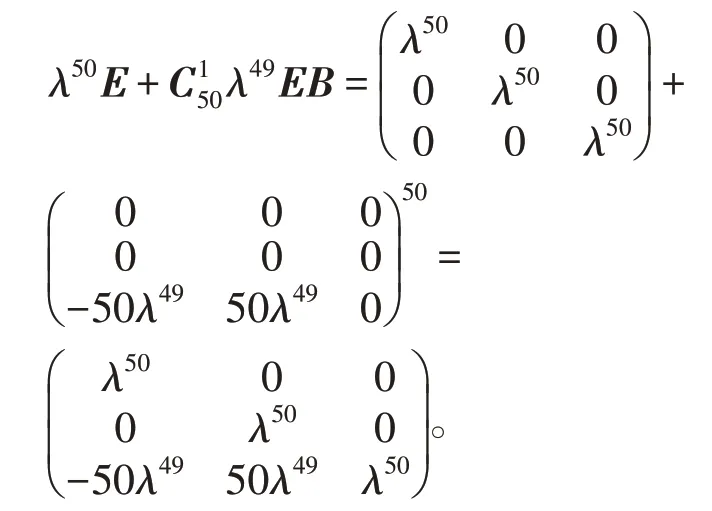
该方法首先要把矩阵A写成两个矩阵B,C的和，并要求这两个矩阵满足(1)矩阵B,C可交换；（2）其中一个矩阵的较低次幂的结果为特殊矩阵，如：零矩阵，数量矩阵，故此方法具有很强的技巧性，适用范围有限。

3 利用初等变换

若A为初等方阵,则An可以看成连续进行同一初等变换得到。

例3计算

解可以看成在第一个矩阵右边乘了2015个第三种初等矩阵，即相当于对第一个矩阵作了2015次把第一列加到第二列的初等变换，于是

4 利用相似矩阵

如果矩阵A能够相似对角化，即存在可逆矩阵P，使得P-1AP=Λ，其中Λ为对角阵，从而A=P-1AP,于是有

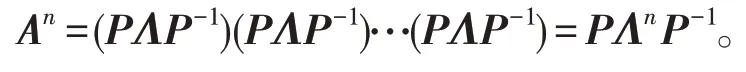
例4设求An。

解A的特征多项式为

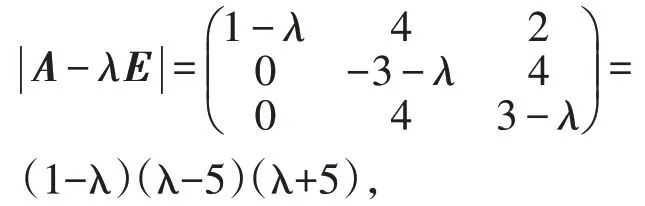
所以A的全部特征值为λ1=1,λ2=5,λ3=5，

分别将λ1=1,λ2=5,λ3=5 代入方程 (A-λiE)x=0(i=1,2,3)，可求得它们对应的特征向量分别为

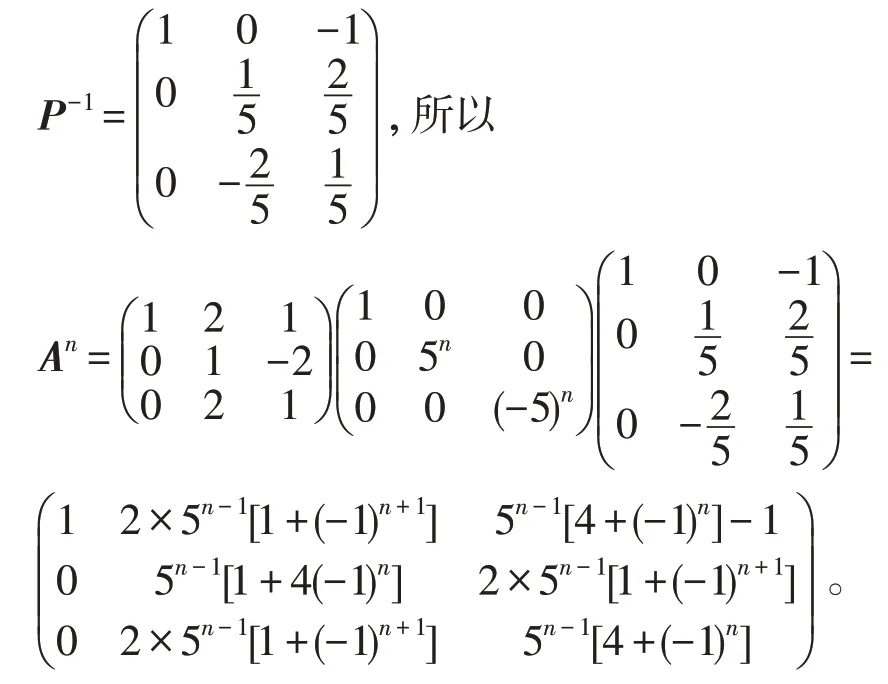
虽然利用对角矩阵计算矩阵的高次幂具有一般性，但是此方法不仅要求矩阵的特征值，还需要求矩阵的特征向量，对于高阶矩阵来说还是比较困难的。为此，能不求特征向量，降次方法能达到求n阶方阵高次幂。

5 矩阵分解法

若矩阵A的秩为1，则A可分解成一个列向量与一个行向量的乘积，然后再利用此分解式计算。

例5求

解记易知R(A)=1, 从而A可以表示为一个列向量和一个行向量的乘积，显然记α=(1 2 3) ，则从而A=αTα，但注意到ααT=14，故

这类矩阵A的特征是至少存在一个非零行向量，使得其余行向量都能用这个行向量来线性表示，因此矩阵A总是可以化为一个n维列向量α=(a1,a2,...,an)T和一个n维行向量β=(b1,b2,...,bn)的 乘 积 ，即A=αβ所 以An=(αβ)n=α(βα)n-1β=

6 利用哈密顿-凯莱定理

哈密顿-凯莱定理为:若A为n阶方阵,它的特征多项式f(x)=|xE-A|=xn+a1xn-1+…+an，

则f(A)=An+a1An-1+…+anE=0。

例6设求An。

解因|λE-A|=λ3-λ2-λ+1，

由哈密顿-凯莱定理有

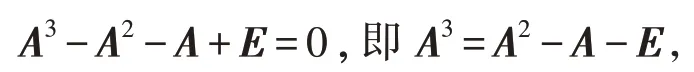
假设An-1=An-3+A2-E，两边乘A，有

令n=100，有

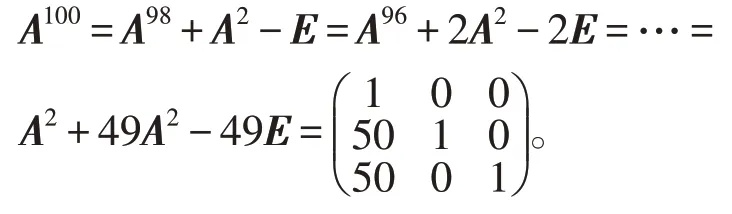
求方阵的高次幂的防范还有很多，在求解的过程中一定要根据所给矩阵的特点，选择适合的最简单的方法。