双凯莱图的完全完备码

李建勋,王 燕

(烟台大学数学与信息科学学院,山东 烟台 264005)

完备码(图论中也称为有效控制集)问题是基于图中顶点集合划分提出的,目的是利用图中的孤立点集将所有顶点进行划分。这种划分也是图模拟网络进行稳定性研究的一个重要方面。而完全完备码是利用图中的匹配来代替孤立点集来划分图的顶点集合,这样也增加了网络的稳定性。

定义1假定Γ是一个图,T是顶点集V(Γ)的一个子集。若Γ的每一个点都与T中的唯一的一个点相邻,则称T是Γ的一个完全完备码。

由定义可知,T中每一个点也恰好和它内部的一个点相邻,因而T是一个匹配。近些年来,点传递图尤其是凯莱图中的完全完备码问题受到了广泛关注。例如文献[1]刻画了二部凯莱图的完全完备码,并给出了某些循环Harary图存在完全完备码的充要条件。文献[2]给出了有限群的一个共轭封闭子集构成该群的凯莱图的完全完备码的充要条件。文献[3]给出了完备码个数为2的方幂的循环图存在完全完备码的充要条件以及给出了子群可作为完全完备码的一个充要条件。文献[4]刻画了奇素数度循环图中存在完全完备码的充要条件。文献[5]讨论了循环群上4度凯莱图的完全完备码问题。关于交换群上的凯莱图,文献[6]给出了交换群上4度凯莱图存在完全完备码的充要条件。

本研究关注双凯莱图完全完备码的存在性问题。一般来说,双凯莱图不是点传递图,但是它是最接近点传递图的一类图。

定义2设H是一个有限群,R,L,S是H的子集合,满足1∉R∪L,R=R-1,L=L-1。定义H关于R,L,S的双凯莱图,记作Γ=BiCay(H;R,L,S)。其中Γ的点集合V(Γ)=H0∪H1,Hi={hi|h∈H},i=0,1,边集合E(Γ)={{h0,(xh)0},{h1,(yh)1},{h0,(zh)1}︳x∈R,y∈L,z∈S}。特别地,如果R=L=∅,则称Γ是一个Haar图,关于Haar图,可以参考文献[7]。

第1节,列出了双凯莱图及完全完备码的一些基本性质。第2节给出了正则双凯莱图的一个顶点子集合是完全完备码的几个等价条件。作为第2节主要结果的应用,第3节考虑了一些特殊的完全完备码。

1 预备知识

从定义可以比较容易推出连通双凯莱图的以下基本性质。

引理1[9]设H是一个有限群,R,L,S是H的子集合,满足1∉R∪L,R=R-1,L=L-1,Γ=BiCay(H;R,L,S)是H的一个双凯莱图。如果Γ连通,则以下结论成立:

(1)H由R∪L∪S生成。

(2) 在同构的意义下可以假定S中包含H的单位元。

(3) 对任意的α∈Aut(H),BiCay(H;R,L,S)≅BiCay(Hα;Rα,Lα,Sα)。

(4)BiCay(H;R,L,S)≅BiCay(H;L,R,S-1)。

在有限群H中,任取H的两个子集U和V,若U与V都非空,则令UV={uv|u∈U,v∈V},否则UV=∅。特别地,如果U={u}或V={v},则记UV=uV和UV=Uv。显然,UV⊆H。

设Γ=BiCay(H;R,L,S),|R|=|L|,α是H上一个既单且满的映射满足(1H)α=1H且Rα=L。任取T⊆V(Γ),则T=M0∪N1,其中M和N是H的子集。令T*=M1∪N0,称T*是T的共轭集。对任意的x∈R,令x∘αT=(xM)0∪(xαN)1;当S=S-1时,令x·T*=(xM)1∪(xN)0,否则令x·T*=(xM)1∪(x-1N)0。如果K⊆H,令K∘αT=∪k∈Kk∘αT和K·T*=∪k∈Kk·T*。对于任意h∈H,NΓ(h0)和NΓ(h1)分别表示h0与h1在Γ中的邻点集合,则有

NΓ(h0)={(rh)0,(sh)1|r∈R,s∈S},

NΓ(h1)={(rαh)1,(s-1h)0|r∈R,s∈S}。

显然,∪t∈TNΓ(t)=∪x∈R,y∈S(x∘αT∪y·T*)。

由定义可以直接得到命题1和命题2,省略证明。

命题1假定Γ=BiCay(H;R,L,S)是一个正则的双凯莱图,T=M0∪N1⊆V(Γ),α是H到自身的一个既单且满的映射且(1H)α=1,Rα=L。则T是一个α-拟正规子集当且仅当对任意x∈R,xM=Mx,xαN=Nx,对任意的y∈S,yM=My,且当S≠S-1,y-1N=Ny,当S=S-1,yN=Ny

命题2Γ是一个图,有下面三个结论成立。

(1) 如果T是Γ的完全完备码,则V(Γ)的|T|个子集,NΓ(t),t∈T是V(Γ)的一个划分。

(2)T0,T1是Γ的两个无公共点的完全完备码,则|T0|=|T1|,且T0∪T1在Γ中的诱导子图是一系列无交偶圈的并。

(3)T是Γ的完全完备码,对任意的σ∈Aut(Γ),(T)σ也是Γ的完全完备码。

2 双凯莱图的完全完备码

定理1揭示了正则双凯莱图的完全完备码与图的点划分的密切联系。

定理1假定H是有限群,Γ=BiCay(H;R,L,S)是H的一个正则双凯莱图。令T⊆V(Γ),T=M0∪N1,M与N是H的子集。则对任意的一个H到自身的既单且满的映射α,满足(1H)α=1H且Rα=L,下述结论(1)和结论(2)等价。此外,若α∈Aut(Γ),S=S-1,那么结论(3)也与结论(1)、(2)等价。

(1)T是Γ的完全完备码。

(2)T⊆V(Γ)的|R|+|S|个子集,x∘αT,y·T*是V(Γ)的一个划分,其中x∈R,y∈S。

证明注意到(1H)α=1H,1H∘αT=T。

(1)⟹(2):假定T=M0∪N1是Γ的一个完全完备码,则T是一个匹配。根据命题2,V(Γ)的|M|+|N|个子集NΓ(m0),NΓ(n1),m∈M,n∈N是

V(Γ)的一个划分。因为NΓ(m0)={(rm)0,(sm)1|r∈R,s∈S},NΓ(n1)={(rαn)1,(s-1n)0|r∈R,s∈S},这表明V(Γ)的|R|+|S|个子集,x∘αT,y·T*是V(Γ)的一个划分,其中x∈R,y∈S。

(2)⟹(1):假定V(Γ) 的|R|+|S|个子集,

x∘αT,y·T*是V(Γ)的一个划分,其中x∈R,y∈S,则V(Γ)=∪t∈TNΓ(t)。而且对任意的a∈V(Γ),存在唯一的r∈R,唯一的m0,n1∈T,使得a=(rm)0或(rαn)1;或存在唯一的s∈S,唯一的h0,k1∈T*,使得a=(sh)1或(s-1k)0,因此|NΓ(a)∩T|=1。故T是Γ的完全完备码。

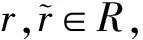
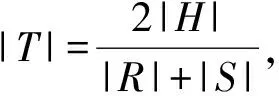
注1 在引理1中虽然可以根据图同构来假设1H∈S,但是该条件的存在与否会使得V(Γ)的子集有非常大的差异。在定理1的结论(2)中,若1H∈S,则T*是这些|R|+|S|个子集中的一个。反之,T*不一定在这些子集中。

当T是一个完全完备码时,通过计算H0,H1包含在x∘αT,y·T*,x∈R,y∈S中的点就可得到T*与H的联系。

推论1Γ=BiCay(H;R,L,S)是正则的双凯莱图,T=M0∪N1是Γ的一个完全完备码,有下述结论成立:

(1) 当M和N都不为空集,且|R|≠|S|时,有

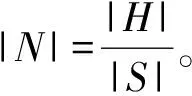
证明根据定理1得,T是Γ的完全完备码,则V(Γ)的|R|+|S|个子集,x∘αT,y·T*是V(Γ)的一个划分,其中x∈R,y∈S,α是H到自身的既单且满的映射,(1H)α=1H且Rα=L。

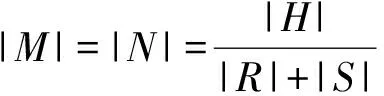
注意若T是Γ的完全完备码时,T的共轭不一定是Γ的完全完备码。但是,在一定条件下,T和T*可以同时是完备码。

引理2Γ=BiCay(H;R,Rα,S)是正则双凯莱图,其中α∈Aut(Γ)。令T⊆V(Γ),T=M0∪N1,M与N是H的子集。如果Mα=M,Nα=N,S=S-1,则T是完全完备码当且仅当T*是完全完备码。特别地,在Haar图Γ=BiCay(H;∅,∅,S)中,只要S=S-1,则T是完全完备码当且仅当T*是完全完备码。

证明假定T是完全完备码。任取h0∈H0,则有(hα)1∈H1。由条件α∈Aut(Γ),Mα=M,Nα=N,S=S-1,则存在唯一的r∈R,n∈N使得(hα)1=(rαnα)1,或唯一的m∈M,s∈S,使得h1=(sm)1。因此h0=(rn)0或(sm)0,r,n,m,s都是唯一确定。考虑到S=S-1,故T*中有且只有一个点与h0相连。对于任意的h1∈H1,同理可得T*有且只有一个点与h1相连。当T*是完全完备码时,同理可证T是完全完备码。

在Haar图Γ=BiCay(H;∅,∅,S)中,假定S=S-1。如果T是Γ的完全完备码,任取h0∈H0,则h1∈H1而且存在唯一的m∈M,s∈S,使得h1=(sm)1,因此h0=(sm)0,即T*中有且只有一个点与h0相邻。对于任意的h1∈H1,同理可得T*有且只有一个点与h1相连。因此,T*是完全完备码。同理可证如果T*是完备码,那么T也是完全完备码。

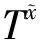
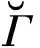
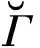
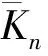
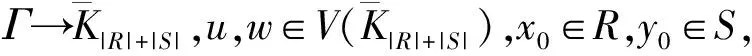
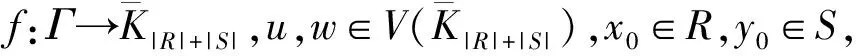
作为一种特殊的情况,下述推论3显然成立。

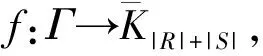
在Haar图Γ=BiCay(H;∅,∅,S)中,如果T=M0∪N1是完全完备码,则对于M0或M1中任意一个点都有N1或N0中的唯一个点与之相邻,反之亦然。再根据命题1,T是α-拟正规子集当且仅当对任意s∈S,sM=Ms,sN=Ns。令Kn×n表示具有2n个点的完全二部图,则有如下结论。

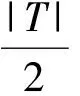
通过上述结论,最终可得到定理4。

定理4Γh=BiCay(H;∅,∅,S),T=M0∪N1是V(Γ)的一个子集,S=S-1,对任意s∈S,有sM=Ms,sN=Ns,则下面条件等价:

(1)T是Γh的完全完备码。

(2)V(Γh)的2|S|个子集(sM)1,(sN)0是V(Γh)的一个划分,其中s∈S。

(4) 存在覆盖映射f:Γ→K(S,S)=(U,W),u,w∈V(KS,S)使得f-1(u)=(sM)1且f-1(W)=(sN)0。

3 子群完全完备码

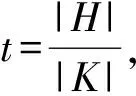
定理5 假定H是有限群,K是H的子群且K有一个逆封闭的左横贯S。则对任意的L⊆H,K0是双凯莱图Γ=BiCay(H;S,L,S)的一个完全完备码。

证明因为2|S|个子集(rK)0,(sK)1,r,s∈S是V(Γ)的一个划分。根据定理1,对任意的L⊆H,K0是Γ的完全完备码。

定理6 假定H是有限群,K是H的子群,Γ=BiCay(H;R,Rα,S)是一个正则双凯莱图,其中α是H到自身的一个既单且满的映射且满足(1H)α=1H。对任意的h∈H,下述结论成立。

(1)T=K0∪(Kh)1是Γ的完全完备码,当且仅当H可以被划分成|R|+|S|个子集rK,s-1Kh,r∈R,s∈S,也可以被划分成|R|+|S|个子集sK,rαKh,r∈R,s∈S。

(2)T=K0∪K1是Γ的完全完备码,当且仅当H可以被划分成|R|+|S|个子集rK,s-1K,r∈R,s∈S,也可以被划分成|R|+|S|个子集sK,rαK,r∈R,s∈S。

证明根据定理1,T是Γ的完全完备码,当且仅当|R|+|S|个子集,r∘αT,s·T*是V(Γ)的一个划分,其中r∈R,s∈S。因为r∘αT=(rK)0∪(rαKh)1,当S=S-1时,有s·T*=(sK)1∪(sKh)0,否则s·T*=(sK)1∪(s-1Kh)0。因此,H0=(rK)0∪(s-1Kh)0和H1=(rαKh)1∪(sK)1,故结论(1)成立。

因为Kh=K当且仅当h∈K,所以结论(2)是结论(1)的特殊情况。

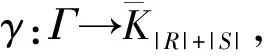
证明令α作为H的一个单位自同构,根据命题1,T是一个α-拟正规子集。显然Mα=M,Nα=N。又有S=S-1,根据推论3可得上述结论。