非圆齿轮系统在火炮系统上的应用
2020-04-02牛瑞利王国虎
牛瑞利,王国虎
(郑州工业应用技术学院机电工程学院,郑州 451100)
0 引言
轮系是由一系列相互啮合的齿轮来满足工作要求,是一种常见且经典的传动装置,轮系具有大传动比的传动、远距离的两轴传动和换向传动、分支传动以及运动的合成和分解等特点。学者们虽然针对齿轮开展了诸多研究(见文献[1-6]),然而都是针对圆形齿轮开展的;由于非标齿轮通常是按企业的要求而量身设计、定制的,针对某火炮转动装置的需求,由于功能的限制,传统的圆形齿轮已经无法满足使用要求,因此,基于其工作特点,设计了一套非圆齿轮的传动系统装置。以非圆齿轮系统为研究对象,首先使用Solidworks 软件进行结构设计,然后建立数学模型进行理论推导和分析;最后利用Adams 仿真分析,得到其运动规律和动力学性能曲线,为以后的结构优化设计提供参考依据。
1 非圆齿轮工作原理
非圆齿轮系统主要有太阳轮、行星轮和固定轮组成。其结构原理图如图1 所示。
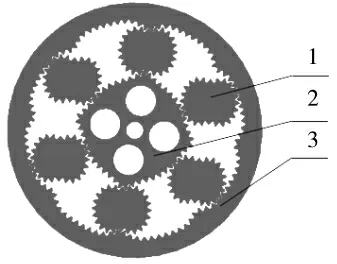
图1 非圆齿轮系统组成
由图1 可知,在电机的转速作用下,太阳轮随之转动;为了转动装置的效率,设计了6 个行星轮与太阳轮和固定轮啮合。在太阳轮、行星轮以及固定轮的联合作用下,行星轮实现变轴线的啮合运动。
2 数学模型的建立
建立非圆齿轮系统的数学模型时可以分为扭转振动模型和平移-扭转耦合振动模型[7]。由于扭转振动模型为考虑齿轮系统的传动轴和轴承的影响,不能准确预测齿轮系统的结果。为了方便对模型进行描述,以太阳轮的中心为原点建立笛卡尔坐标系,系统的坐标系随着行星架的转动而转动。非圆齿轮轮系各构件如图2 所示。

图2 非圆齿轮轮系各构件组成
为方便对非圆齿轮轮系进行描述,选取ui(i=c,r,s,1,2,…,N)、θi(i=c,r,s,1,2,…,N)以及ri(i=c,r,s,1,2,…,N)分别表示固定轮、太阳轮以及行星轮的位移、角位移和基圆半径。系统的广义坐标可以表示为:

非圆齿轮系统是由6 个行星轮组成的,鉴于方法一样,在此对一个行星轮和太阳轮以及固定轮组成的系统进行分析。利用拉格朗日方程对非圆齿轮系统进行动力学方程推导,可以得到以下方程组。

式中:mr为太阳轮的质量,ωc为太阳轮的角速度,Fm为齿轮间的啮合力,为第n 个行星轮中心和行星架中心连线与xc正方向的夹角,;Jr为太阳轮的转动惯量,cru和crz为第n 个行星轮与太阳轮、内齿圈的啮合阻尼,kru和krz为第n 个行星轮与太阳轮、内齿圈的啮合刚度。
由于齿轮之间存在间隙,非圆齿轮系统之间存在相对位移,即弹性变形量。在行星架随动坐标系下,考虑啮合误差的构件间相对位移可表示为:

si(i=1,2)为第n 个行星轮与太阳轮、内齿圈在各自啮合线方向的相对位移,si(i=3,4,5,6)为行星轮与行星架在xc、yc、zc和uc方向的相对位移,si(i=7,8)为行星轮与行星架在xn和yn方向的相对位移。
3 动力学模型的建立
3.1 模型的建立
建立动力学模型的方法可分为两类:一种是使用Adams 自身建模功能对其建立模型,主要用来对简单模型或者标准件(如齿轮、轴承)进行建模;另一类方法是利用三维建模软件(如SolidWorks/UG等)进行建立模型,然后保存为中间格式将其导入Adams,再使用修复功能将失真较大的零件进行修整,最后得到动力学模型。本文为了能够准确得到非圆齿轮的结构,采用第2 类方法对非圆齿轮系统建模,最终完成对非圆齿轮系统的动力学建模。
3.2 约束与驱动的添加
在完成动力学建模后,需要对模型进行添加约束和驱动,为了方便对模型进行仿真,对模型进行以下的简化和假设[8-9]:1)将电机的转速换成输入传动系统时的转速,减速器的减速过程忽略;2)忽略模型的尺寸公差和安装误差,且所有齿轮作为刚体考虑[10]。
按照实际情况对模型进行添加材料和约束,即在齿轮与齿轮之间添加接触约束,其中固定轮添加固定约束,其余齿轮均与大地之间添加旋转副;然后将换算好的转速添加至太阳轮上。
在Adams 中,根据Impact 函数来计算两个构件之间的接触力时,接触力由两部分组成:一个是由两个构件之间的相互切入而产生的弹性力;另一个是由相对速度产生的阻尼力[11-14]。表达式如下:

式中:K 为Hertz 接触刚度,δ 为渗透量,dmax为允许的最大穿透深度,cmax为当达到最大穿透深度时的最大阻尼值为接触点的法向相对速度。
4 仿真与结果
非圆齿轮系统的传动性能对某火炮的转动装置有着重要的影响,由齿轮啮合相关知识可知齿轮之间存在间隙,因此,需要考察非圆齿轮系统在空载时行星轮的速度和角速度曲线变化。
由图3 和表1 可知,非圆齿轮之间的间隙对行星轮速度影响最大的是X 轴方向,其范围是±450 mm/s左右,主要原因由于X 轴是非圆齿轮啮合传动动力前进的方向,影响最小的是齿轮旋转的轴线Z向,最大值为157.9 mm/s,说明齿轮系统存在振动。

图3 行星轮的速度曲线

图4 行星轮的角度速度曲线

表1 行星轮的速度
由于非圆齿轮系统存在振动,齿轮在啮合的过程中,行星轮在径向和周向方向的速度均不为零。图4 和表2 的数据可知在齿轮传动动力时,Z 向的角速度波动最小,主要原因是因为行星轮在太阳轮和固定轮的相关配合,行星轮在啮合力的作用下绕着太阳轮运动。

表2 行星轮的角度速度
齿轮传动主要依靠的是齿轮之间的啮合力,行星轮与太阳轮之间的啮合力如图5 和表3 所示。

图5 行星轮与太阳轮的啮合力

图6 行星轮与固定轮的啮合力

表3 行星轮与太阳轮的啮合力
由图5 和表3 可知,行星轮与太阳轮的最大啮合力为245.9 N,整体是在±100 N 左右波动;其中在周向方向的接触力要略大于径向的作用力。行星轮最终在周向和径向的联合作用力下,实现圆周运动。

表4 行星轮与固定轮的啮合力
由图6 和表4 可知,行星轮与固定轮之间的最大啮合力为364.5 N,其发生在0.64 s,此时在径向上的接触力为199.4 N。相比行星轮与太阳轮之间的接触小要略大,造成这一现象的主要原因是由于行星轮所受重力造成的,为了减小其啮合力,可以在齿轮之间增加润滑油,进而减小摩擦力。
综上所述,在满足火炮转动装置非圆齿轮系统的性能的前提下,适当在齿轮之间增加润滑装置可以有效降低齿轮之间的摩擦力,同时也可以提高非圆齿轮系统的性能。
5 结论
基于某火炮转动装置的性能需求,设计了非圆齿轮传动系统;根据非圆齿轮系统的原理进行了数学建模分析和动力学推导,得到了其运动方程;运用Adams 动力学软件对其进行了动力学性能仿真验证,得到了其动力学曲线。
基于仿真结果可知,行星轮与太阳轮之间的接触力要比行星轮与固定轮之间的接触力要小,适当在齿轮之间增加润滑装置可以提高非圆齿轮系统的性能。
通过对非圆齿轮系统动力学性能的研究,不仅得到了非圆齿轮系统的运动规律和动力学曲线,而且对以后的非圆齿轮结构改进设计提供参考依据。
