免疫教与学算法在航空器优化排序中的应用

李 阳，聂党民，温祥西

（空军工程大学空管领航学院，西安 710051）

0 引言

航空器进场排序与调配是对将要进场的航空器按照一定的规则和标准，使之形成一个有着一定先后顺序的航空器进场队列，根据航空器的排序结果，为航空器分配合适的进场时机、着陆时间等，实现进场航空器的安全有序运营。

目前管制指挥员对于进场航空器的指挥调配主要是基于经验，采用先到先服务（FCFS）策略，为进场航空器确定着陆顺序。该策略易于操作，且具有公平公正的特点。随着近几年经济的快速发展，空中交通流量持续增长，传统调配手段低效的缺点越来越显著，航空器延误、空域拥堵的问题日益突出。进场航空器优化排序与调配成为当前研究的热点问题之一［1-2］。

进场航空器优化排序的要点在于保持航空器之间安全间隔，根据一定的约束条件，为进场航空器进行重新排序与调配，以期达到提升跑道容量、减少延误、减轻管制员工作负荷的目的。智能算法作为一种启发式算法，近年来得到迅猛的发展，被广泛应用于解决航空器优化排序与调配的建模问题。2014 年，杜实［3］等人针对终端区航班延误问题，建立以系统运行时间最短目标函数的元胞传输模型，给出合理的航空器进场排序；同年，徐兆龙［4］等人采用蚁群算法对所建立多跑道航班协同调度多目标动态优化模型进行仿真，降低了航空器进场的延误损失；2016 年，马卫平［5］等人利用蚁群算法的全局搜索能力，结合CPS 确保调度的可操作性和公平性，在较短时间内有效减少着陆航班的总延迟时间；2015 年，陈金良［6］等人运用改进人工鱼群算法，建立了以总飞行成本最小为目标函数的多跑道机场进场航班排序模型，有效地缓解了航班延误，降低了飞行成本；同年，马英钧［7］等人针对传统粒子群算法缺点，提出改进策略，解决了航班降落调度的问题；2016 年，张维杰［8］等人提出了一种改进的遗传算法，引入交叉掩码，降低了飞机队列总延误代价；2016 年，陈文平［9］等人基于滚动时域的遗传-免疫算法（RHC-HGIA），解决了滚动时域长度和航班排序优化的问题。

这些算法都可以应用于解决进场航空器优化排序问题，取得了较好的结果，但算法本身拥有一定的局限性，如都需要设置一定的控制参数，参数的选取对于算法的搜索能力会产生较大的影响。教与学优化算法（Teaching-Learning Based Optimization，TLBO）是Rao［10-11］等人于2010 年提出的一种新的种群智能优化算法。该算法通过模拟教师的教学过程和学员的学习过程来实现，因其简单、具有更快的收敛速度，收敛能力强，取消了其他智能算法需特定的控制参数值而受到广泛关注。本文通过对该算法进行改进，增加离散化［12］过程，并结合免疫算法的“抗体注入”与“免疫修正”，提出免疫教与学算法（ITLBO），使其可以应用于进场航空器的离散化排序问题，并进行仿真实验分析，来验证该方案的有效性。

1 问题描述

假设机场只有一条跑道，只考虑着陆队列，进场航空器可以从几条不同的航路进入机场着陆，所有的航空器都可以按照进场时间排成一个队列，在航空器终止调配前进行重新排序。

假设该进近段待排序航空器有n 架，集合为F={F1，F2，…，Fn}。定义航空器i 的预计到达时间为ETAi，实际到达时间为STAi。

航空器类型可分为3 种，分别为重型（H）、中型（M）、轻型（L），进场航空器通常以时间为基准，以航空器的尾流间隔作为重要参考因素。定义第i 架航空器类型表示为p（i），当i，j 分别为此航路上的前后两架航空器时，两架航空器间的尾流时间间隔为d［p（i），p（j）］，如表1，选用修正后的基于时间量纲的ICAO 雷达尾流间隔标准，其中列表示前机，行表示后机。

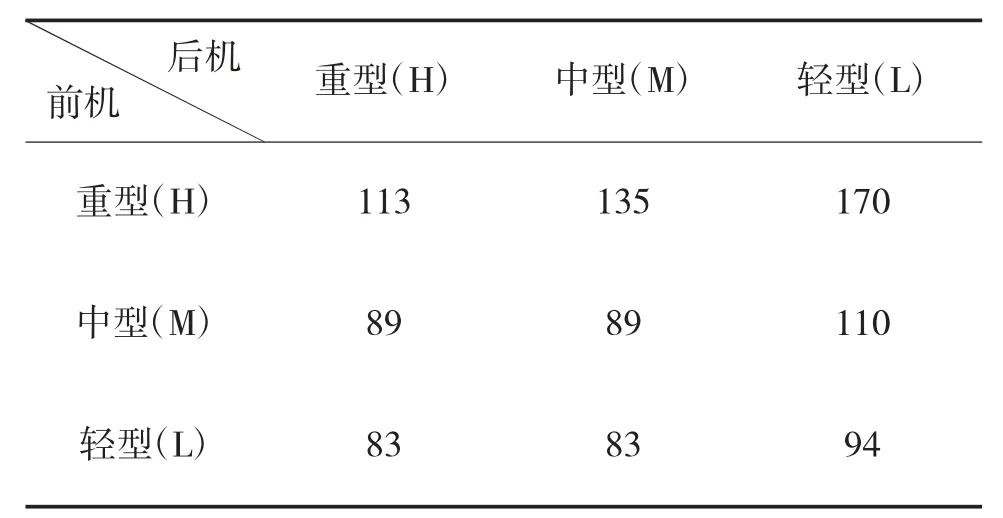
表1 基于时间量纲的ICAO 雷达尾流间隔标准（单位：s）

根据航空器进场序列和雷达尾流间隔标准，可求得航空器的实际到达时间，满足

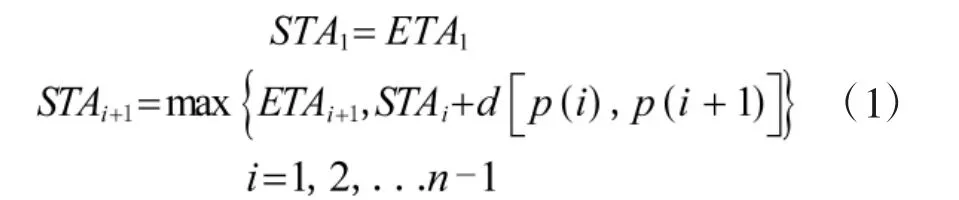
1）目标函数

航空器i 的延误时间表示为D（i），满足

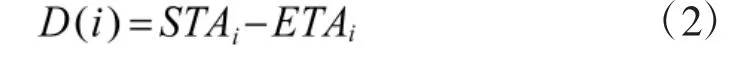
优化目标为最小化航空器平均延误：

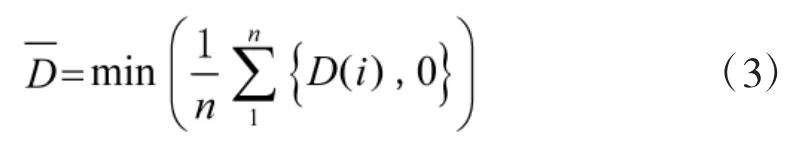
2）约束条件

①间隔要求

航空器在进近着陆阶段，需保持最小安全间隔，该间隔的标准主要取决于航空器的着陆次序以及前后机的尾流标准。满足

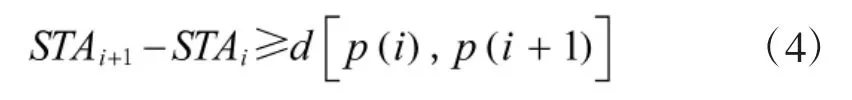
②最大位置约束转换（CPS）

航空器在排序过程中，若重新排成的序列严重偏离FCFS 序列，将增加管制员的管制负荷，同时也不利于航空器的安全运行。因此，需要设置航空器的最大位置偏量。设当前共有5 架航空器，最大位置约束为1 时，航空器位于FCFS 排序的第2 架，则其可能变动的位置有1、2、3。考虑管制员工作负荷及操作限制，一般定义最大位置约束值为1 或2。

2 ITLBO 算法

2.1 基本TLBO 算法

基于教与学的优化算法是模拟以班为单位的学习方式，班级中学员水平的提高需要教师的“教”来引导，同时，学员之间需要相互“学习”来促进知识的吸收。其中，教师和学员相当于进化算法中的个体，而教师是适应值最好的个体之一。每个学员所学的某一科相当于一个决策变量。学员的成绩即函数适应值，教室就是适应值最好的个体。具体定义如下：

1）班级。在TLBO 算法中，将搜索空间中所有点的集合成为班级；

2）学员。班级中某一个点Xj=（，，…，）称之为一个学员；

3）教师。班级中学习成绩最好的学员Xbest称之为教师，用Xteacher表示。

TLBO 算法步骤如下：

1）初始化班级

班级中每个学员

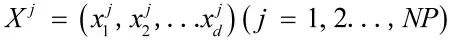
在搜索空间随机生成。

2）“教学”阶段

在TLBO“教学”阶段，班级中每个学员Xj（j=1，2，…，NP）根据Xteacher和学员平均值Xmean之间的差异性进行学习。

采取如下公式进行教学工作：

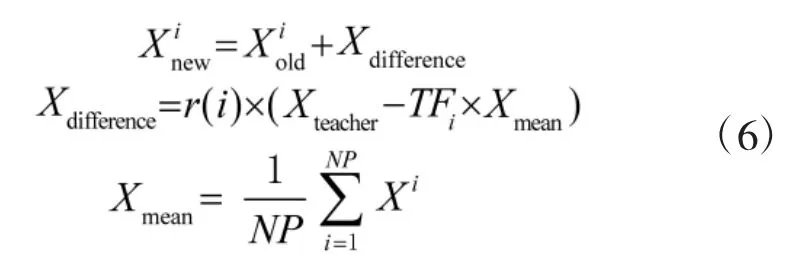
教学完成后，更新学员。对每个学员求取对应的函数适应值，把学习后的成绩和学习之前的成绩进行比较，表达式如下：

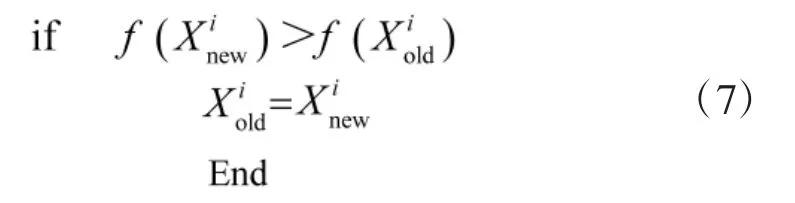
3）相互学习阶段

通过学员之间的相互学习提高，来优化解集。“学”阶段是学员在小范围搜索空间内互相学习，不过会过早向全局最优点靠拢，增强了算法的全局搜索能力，有效保持了种群的多样性。每一个学员在班级随机选取另一个不同学员作为学习对象，相互分析比较来进行更新，采用公式：

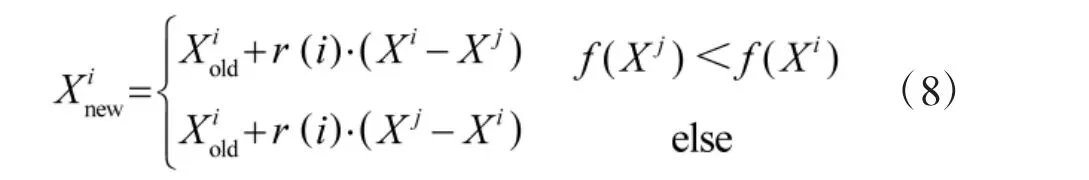
4）如果满足结束条件，则输出结果，否则返回教学阶段继续优化。

2.2 算法改进

传统的TLBO 算法不能直接应用于航空器优化排序问题，需要对算法进行如下改进：

1）离散化

基本的TLBO 主要是针对解决连续问题提出的，航空器排序优化问题属于离散复杂性问题，因此，需要对TLBO 算法进行改进，以解决此类离散优化问题。因此，本文采取的方法是对学员的离散化，即对Xj进行再编译，从而生成新的学员，对新学员进行成绩评定；

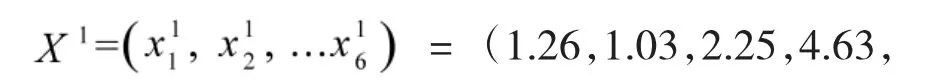
假设第一位学员随机生成6.96，6.21），将该学员生成的随机数按照从小到大升序排列，将排列后的下标作为新的随机数生成新学员。如X1生成新学员。

2）免疫教与学算法

免疫算法［13］模拟了生物免疫的过程，是一种确定性和随机性选择相结合并具有“勘探”与“开采”能力的启发式随机搜索算法。航空器排序过程中，存在最大位置约束转换问题（CPS），需要设定航空器的最大位置偏移量。本文拟引入免疫算法的抗体注入、免疫修正思想，对“教与学”算法进行改进［14-15］，提高其收敛速度及鲁棒性。

在初始化班级过程中，随机产生的序列存在太多不满足约束的可能解，从而影响整个班级的收敛速度，导致算法效率不高。因此，引入免疫算法抗体注入策略，在初始化班级阶段，为随机生成学员提前注入抗体，加入最大位置约束转换（CPS），使得随机生成序列更接近于最佳序列，从而增强算法的收敛能力。

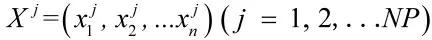
可随机生成n 个包含于搜索空间的数。

3 基于ITLBO 算法的航空器优化排序

1）初始化学员

根据式（9）随机生成初始班级学员Xj，数量为NP。依据离散规则，对初始化的班级学员进行离散化，得到新学员Yj，即为航空器进场排序问题可行解；

2）成绩评定

依据新学员Yj对应的航空器排序序列，参照航空器类型、航空器雷达间隔标准，根据式（1）可求得各架航空器对应到达时间STAi，依据式（2）可求得各架航空器延误时间D（i）。因为航空器优化排序模型优化目标为最小航空器平均延误，算法寻优搜索设置为空间内最小解，因此，可成绩评定f（Yj）=；

3）“教”阶段。采用式（6）实现“教”阶段，对学员进行离散化，计算成绩并进行对比，依据规则式（10）对学员进行更新；

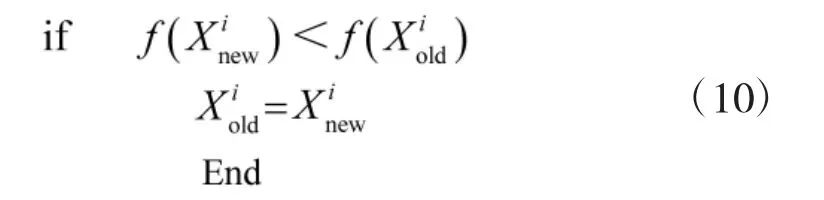
4）“学”阶段。采用式（8）实现班级中学员间的学习，对新旧学员进行离散化，计算成绩并进行对比，依据规则式（10）对学员进行更新，对新生成学员进行免疫疫苗更新；

5）如果满足结束条件，则优化结束，否则转至步骤2）继续。

4 案例分析

以某机场一段时间内的15 架航空器作为样本进行实验。航空器信息如表2 所示。为了检验算法对该模型的可行性和有效性，使用先到先服务排序方法对到场航空器进行仿真分析，结果如下。

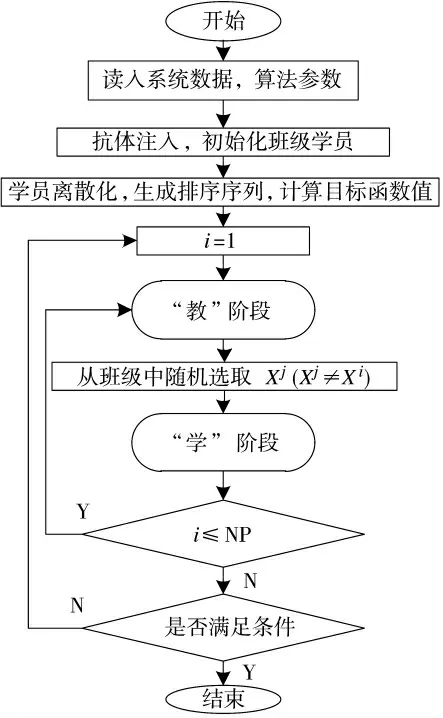
图1 基于ITLBO 算法的航空器排序流程图

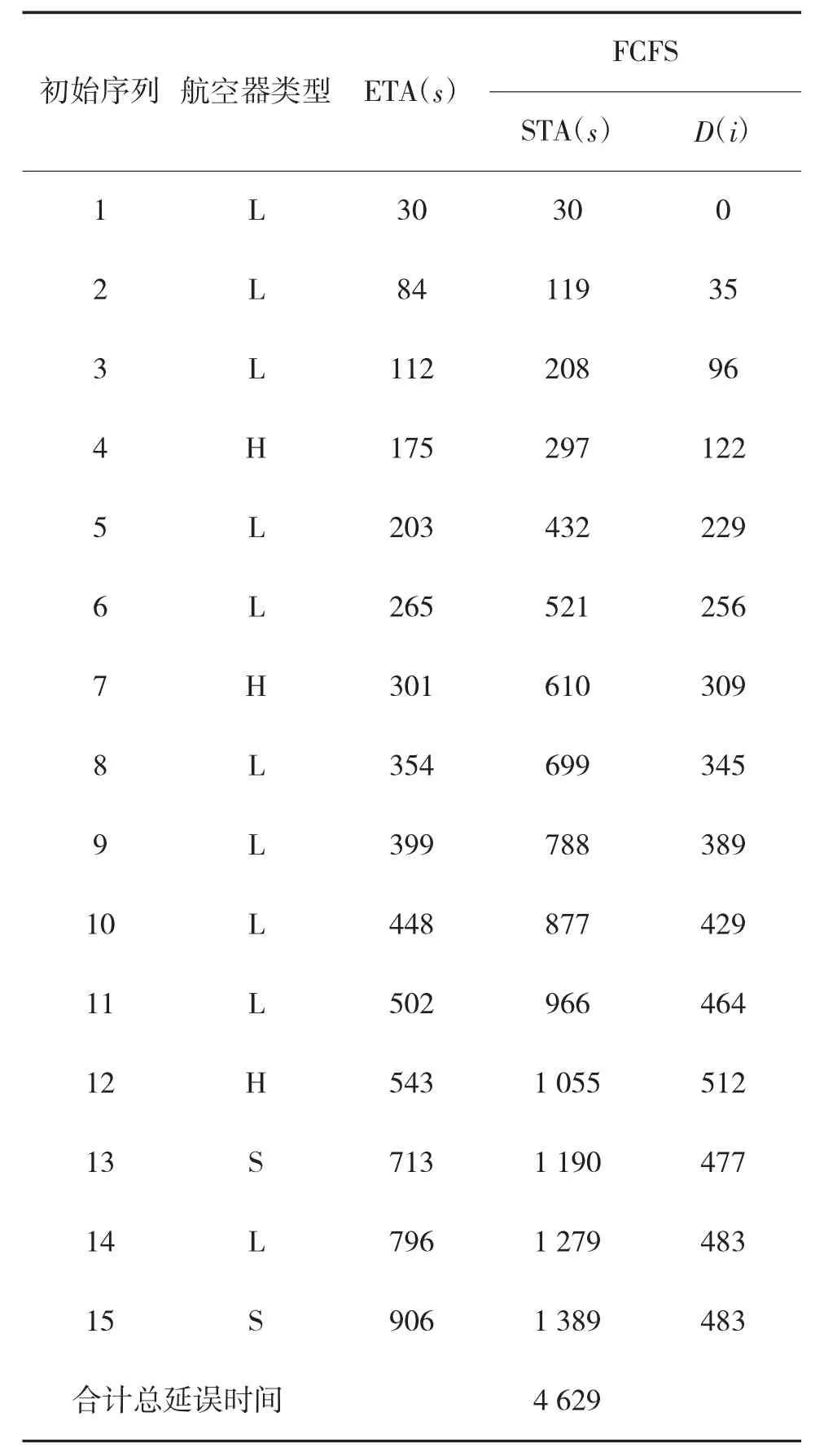
表2 基于FCFS 方法的航空器排序结果

使用ITLBO 算法，设置迭代次数为100 次，学员数为20，CPS=1，进行仿真分析，算法的收敛特性曲线如图2，所得排序结果如表3。

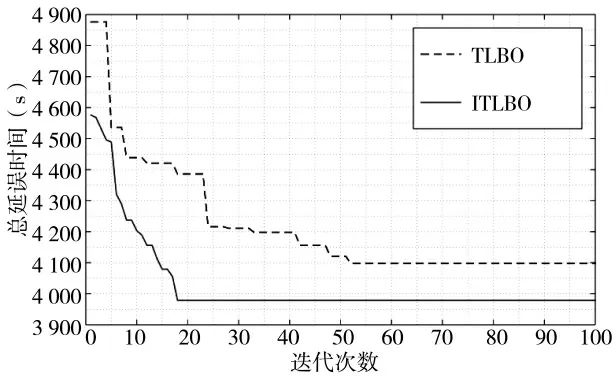
图2 算法收敛特性曲线图

表3 基于ITLBO 算法的航空器排序结果

由表2 与表3 可知，FCFS 方法的航空器优化排序最终延误时间为4 629 s，ITLBO 算法对于进场航空器排序产生的延误时间为3 797 s，ITLBO 算法可以实现对进场航空器的有效排序，并将总延误时间降低了650 s。由图2 可知，ITLBO 算法离散化TLBO算法收敛速度更快，优化效果更好。

仿真表明，经过ITLBO 算法可以应用于进场航空器的优化排序模型中，且求解速度较快，与传统先到先服务调配方法相比延误更小，可以加快航空器的降落时间，降低飞行成本。

5 结论

本文通过对基本TLBO 算法进行离散化处理，结合免疫算法相关思想进行算法改进，并将其应用于解决进场航空器的优化排序模型的离散问题，得出了经过优化后的航空器序列。与传统调配方法相比，使用改进算法进行调配可以更好地解决航空器延误问题，降低飞行成本，提高机场利用率，为航空管制自动化提供一定的技术支持。未来的研究主要以提高算法在各个场景的实用性为主，并基于优化后的调度策略提出相应的调配策略以及辅助工具。