基于虚拟样本与模糊阈值的可靠性评估方法

赵新超，吕卫民

（海军航空大学，山东 烟台 264001）

0 引言

随着当今社会科技水平和制造工艺的日益进步，产品的结构、功能变得越来越复杂，寿命也越来越长，基于寿命数据的传统可靠性评估方法已很难再对这类产品的可靠性作出有效的评估［1］。与寿命数据相比，由产品的性能退化数据可以获得更多的失效信息。

目前，国内外专家学者已经对基于性能退化数据的可靠性评估方法作了很多研究［2-6］，但大多数都局限于单个性能特征参数发生退化的情况。在实际工程应用中，产品往往同时存在多种失效机理、多个性能特征参数一起退化。此外，受限于经费和试验时间，产品的样本数据通常也较少。针对多性能参数产品的可靠性评估问题，也有部分学者作了一些研究，解决方法大致可以分为两种：一是充分考虑性能参数之间的相关性，如联合概率密度法和状态空间法［7-11］；二是基于性能参数距离的可靠性分析方法［12-13］。第1 种方法虽然充分考虑了各个性能特征参数之间的关联性，较好地反映了实际问题，但当参数较多时却存在建模困难、运算量大等问题。第2 种方法虽然能够有效降低运算的复杂度，但多性能参数经过降维处理分析时，失效阈值的确定仍有待进一步研究和完善。

为了解决上述问题，本文提出一种基于虚拟样本与模糊阈值的可靠性评估方法，通过虚拟样本算法扩充样本数据，然后在基于多参数距离分析的可靠性分析方法上引入模糊失效阈值概念，解决失效阈值的确定问题，从而对产品的可靠性作出较为准确的评估。

1 多性能参数距离分析

产品性能的退化往往表现为一个或多个性能特征参数的变化，因此，要对产品工作状态或性能情况作出评价，就需要综合考虑产品的某几个重点性能参数。在实际问题当中，产品性能参数的变化趋势是随着时间单调上升或下降的，时间越长，每个性能参数值与初始性能参数值间的距离越大，因此，性能参数间的距离能够有效地反映出产品性能的变化趋势［12］，可以采用距离分析的方法对产品的可靠性进行评估。

在采用距离分析的方法进行可靠性评估时需作如下假设：

1）产品性能参数的退化是不可逆的；

2）各个性能参数之间相关或独立；

3）当产品的某个退化参数首次达到失效阈值时，则判定产品失效。

1.1 数据标准化

由于产品各个性能特征参数的退化数据属性众多，通常拥有不同的量纲与量级，导致变量的处置范围相差较大。为了能够更好地对产品的多种类型的退化数据进行分析，需要对其进行标准化处理，将特征变量的值变换到［0，1］区间内，标准化公式如下：

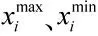
1.2 参数距离模型

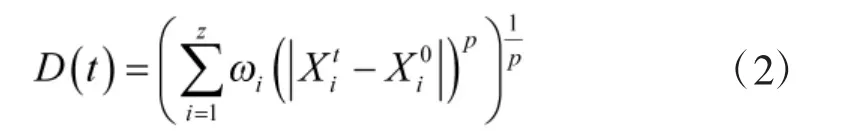
其中，ωi（i=1，2，3，…，z）为加权因子，表示各个特征参数的重要成度；p 为常数，一般取2。

1.3 加权因子的确定

由于产品各个性能参数在实际中的重要程度不同，因此，引入加权因子ωi表示第i 个性能参数的重要度。加权因子ωi可以根据经验或者领域专家给出。当这方面知识和经验较少时，也可以按如下方法求取：

式中，Cov（Xi，Xj）表示Xi和Xj的协方差，Var（Xi）表示Xi的方差，Var（Xj）表示Xj的方差。

根据式（3），依次求取各个性能退化参数之间的相关性系数并取绝对值，就可以得到各个性能退化参数的相关系数绝对值矩阵：

产品性能参数之间的相关性系数的绝对值越大，它们的关联程度就越高，因此，产品性能参数Xi的支持度Sup（Xi）可定义为：

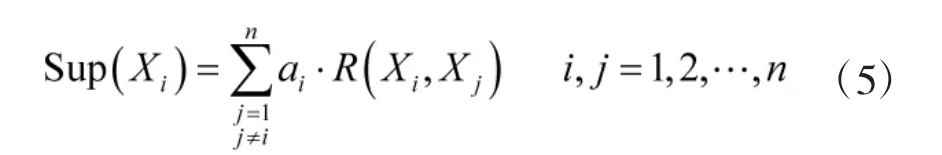
其中，ai为非负数，表示R（Xi，Xj）的权重。

式（5）可用矩阵形式进行表示，如式（6）：

在求得产品性能参数Xi的支持度后，对其进行归一化处理，就可以获得性能参数Xi的权重因子ωi为：

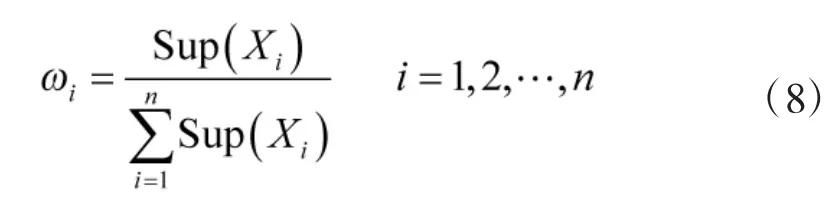
2 虚拟样本

在产品的可靠性评估研究中，受限于试验时间和经费，试验样本的数目往往有限，有时甚至只有一个样本。针对这种情况，文献［14］提出了一种虚拟样本的解决办法，将相对贴近度作为退化特征量，然后对原始样本进行虚拟增广，并对增广得到的虚拟样本数据进行修正处理。该方法虽然扩充了样本数量，但是虚拟样本初始值不一致的问题没有得到解决，导致虚拟样本的退化程度要略大于实际退化程度。

鉴于文献［14］方法存在的不足，本文引入退化速率概念，假设产品在同一时刻具有相同的退化速率，则增广得到的样本数据的退化数据与原样本数据的退化率相同，然后通过改进的Elman 神经网络方法［15］预测退化速率的变化趋势，从而得到各个时刻的退化速率，进而得到各个时刻的退化特征量。

2.1 虚拟样本及退化速率

通过距离分析的方法，可以得到各个时刻的退化数据与初始值之间的距离作为退化特征量，初始样本X0经过1 次退化后，可以将其看作是一个新的初始样本X1，然后分别求出各时刻退化数据相对于X1的距离作为退化特征量，按此法类推，在m 次退化后就能够得到m 个虚拟样本的退化特征量，如表1 所示。

在得到如表1 中的虚拟样本退化特征量之后，可以计算退化特征量的变化速率，定义退化速率v 为：

其中，vij、Dij分别表示编号为i 的退化j 次时的样本退化速率和退化特征量。

表1 虚拟样本退化特征量

由式（9）可得如表2 所示数据。在求得各个时刻的退化速率后，只要初始值已知，就可以反求各个时刻的退化特征量，而初始值已知为0。

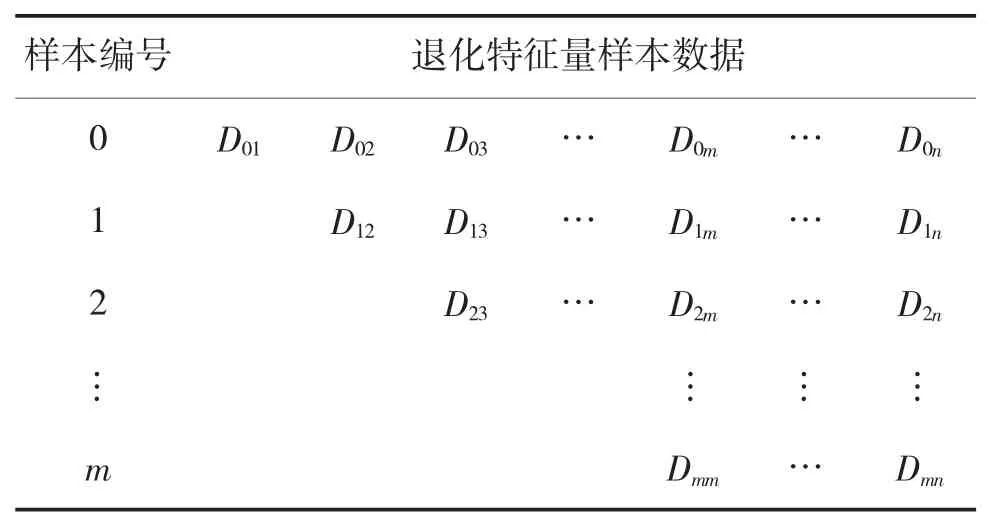
表2 虚拟样本退化速率

2.2 基于Elman 神经网络的退化速率预测

由表2 可以看出，原始样本在m 次退化后能够得到m 个虚拟样本，但第m 个虚拟样本较原始样本会少m 个样本值。为了补齐虚拟样本中的缺失数据，本文采用改进的Elman 神经网络方法［15］，对每个虚拟样本进行处理。

相较于传统的Elman 神经网络，文献［15］中提出的改进Elman 神经网络增加了输出反馈环节，然后将其和隐含层的状态反馈相结合，其结构示意图如图1 所示，经实例检验，改进Elman 神经网络具有更快的收敛速度和更高的预测精度［15］。

图1 改进Elman 神经网络结构示意图

此时改进Elman 神经网络模型为：

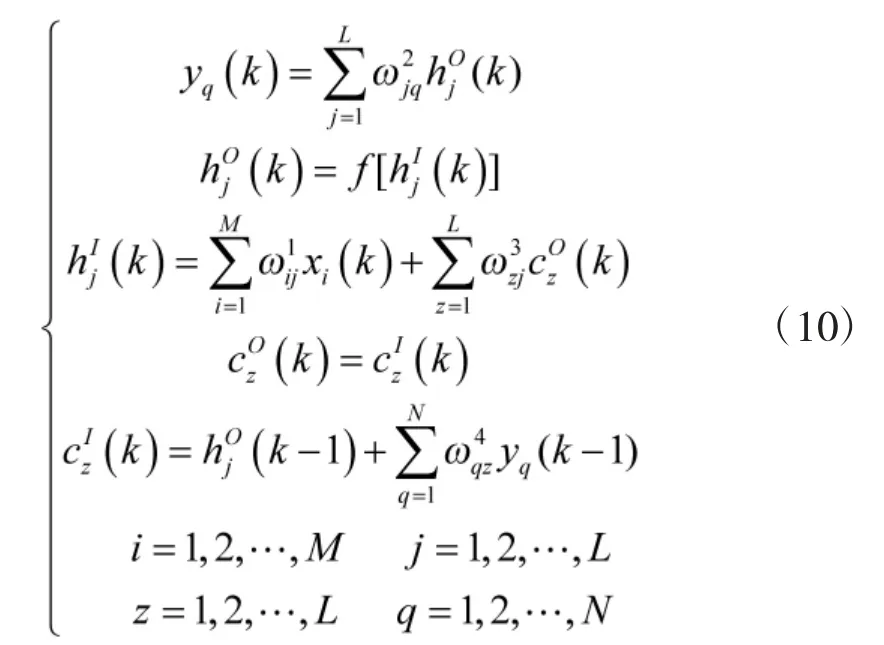
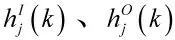
采用改进的Elman 神经网络方法预测虚拟样本缺失数据时，需按如下步骤进行：

2.2.1 获取训练样本

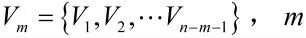
与其相对应的s 个输出向量集为：

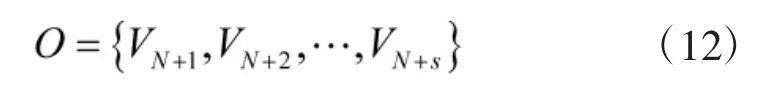
因此，能够得到s 个样本数据：

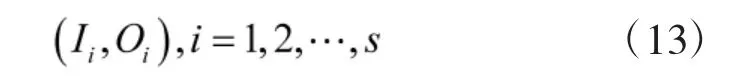
2.2.2 网络结构与网络参数的初始化

在对神经网络进行训练之前，首先要确定神经网络的输入层、输出层和隐含层的节点数以及隐含层数，然后对各层之间的连接权值进行初始化。

2.2.3 网络的训练

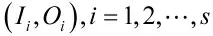
2.2.4 数据预测

若经过测试样本检验该方法的预测结果满足要求，则利用训练好的神经网络对虚拟样本的缺失数据进行预测，进而得到完整的虚拟样本。

3 基于模糊失效阈值的可靠性评估方法

3.1 模糊失效阈值

在传统可靠性评估方法中，失效阈值通常被设定为固定值，当产品的退化特征量达到失效阈值时，则认为产品失效。但是在基于距离分析的多性能参数可靠性评估中，距离分析提取的退化特征量由多个参数共同作用决定，相对应的失效阈值也很难再由某个固定的常数来表达，因此，本文引入模糊概念，将失效阈值模糊化，用来表达失效阈值的不确定性。

模糊集合概念，最早是由美国控制论专家Zadeh 教授提出来的，他将普通集合的特征函数由{0，1}推广到闭区间［0，1］当中，由此定义了模糊集合理论［16］，定义如下：

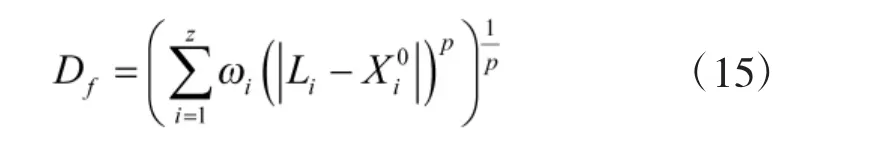
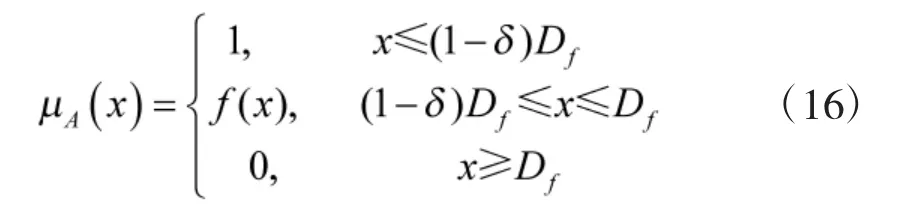
其中，δ 表示波动经验系数，由专家给出。隶属函数中的f（x）可通过F 统计法、三分法、专家经验法等确定，其常用形式有梯形分布、正态分布、三角形分布和π 型分布等。

3.2 可靠性评估方法

假设产品在t 时刻的退化量{xit，t＞0}服从正态分布，产品的阈值为确定值K，因此，产品在t 时刻的可靠度为：

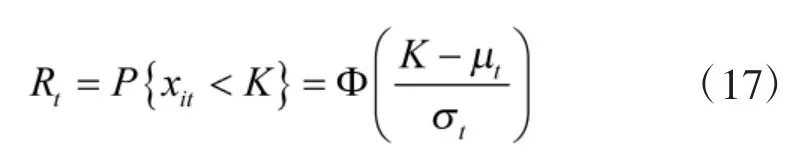
式中，Φ（·）表示标准正态分布函数。μt、σt表示在t时刻退化量的均值参数和方差参数，其估计值为：

根据分布参数估计值随时间的变化轨迹，选择合适的曲线模型，然后估计曲线方程中系数，从而可以预测得到各个时刻的分布参数。

将式（16）和各个时刻的分布参数带入式（17）中可得产品的可靠度为：

根据式（20），再通过MATLB 仿真，就可以得到产品的可靠性退化曲线。

4 实验结果与分析

为了对本文方法的有效性进行检验，选取一台航天继电器作为样本进行加速退化试验，设定温度应力为125℃，分别对航天继电器的接触电阻Rj、吸合时间Tx和释放电压Us3 个特征参数进行测量，得到的退化数据如图2 所示。产品3 个特征参数的失效阈值分别为50 mΩ、8 ms、2.5 V。受外界环境以及测量误差的影响，得到的退化数据可能存在异常值和噪声，因此，有必要对其进行移动平滑处理。

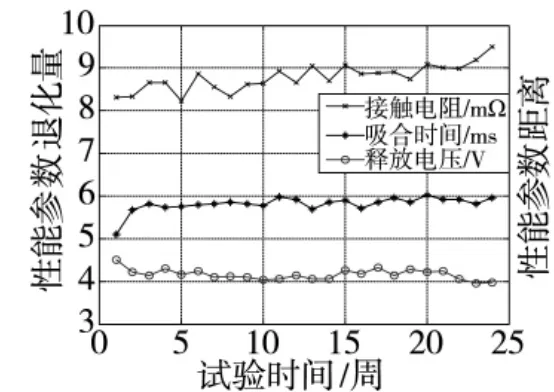
图2 航天继电器特征参数样本数据

图3 距离特征退化量轨迹

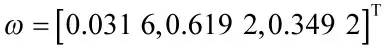
虚拟样本中有部分值是经过Elman 神经网络预测得到的，因此，需要对神经网络的预测精度进行检验。本文以连续10 周的特征量作为输入向量，第11 周的特征量作为目标向量，故可以获得63 组数据。取前50 组数据作为训练样本对神经网络进行训练，并将以后13 组数据作为测试样本对其预测精度进行检验。经检验，神经网络的预测精度较高，结果如图4 所示，因此，由神经网络预测得到的虚拟样本缺失值可信。

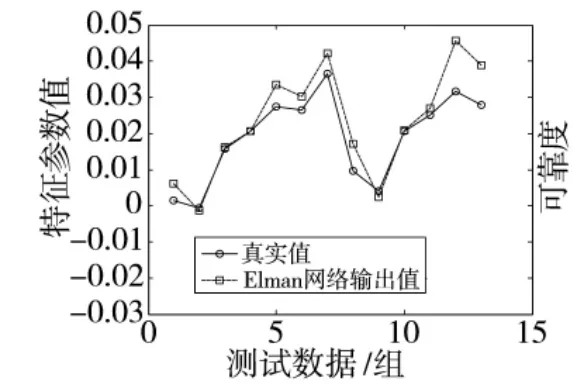
图4 Elman 神经网络预测结果曲线

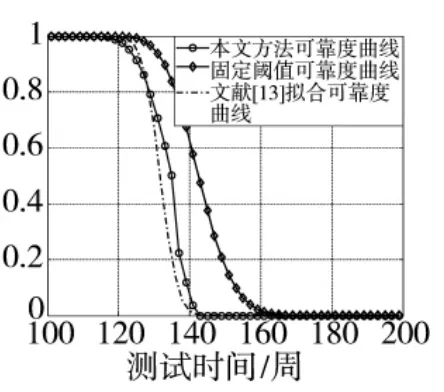
图5 航天继电器的可靠度曲线

再根据第3 节中的方法，求得失效阈值上限Df=7.85，取δ=0.05 可得航天继电器的阈值模糊区间为［7.46，7.85］，假设其隶属函数为降半型，即：

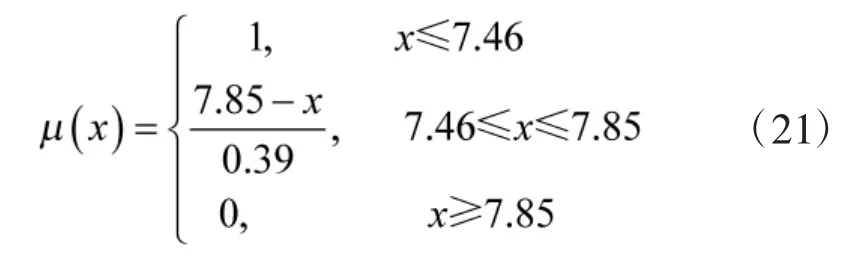
通过式（18）和式（19）可以求出产品退化特征量在各个时刻的分布参数估计值，然后根据分布参数估计值随时间的变化轨迹，选择回归线性模型对其进行拟合，并求出回归线性方程的系数，从而实现对未来时刻分布参数值的预测，其结果如下所示：

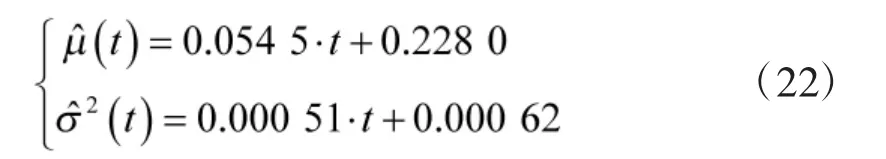
根据式（17）、式（20），并通过MATLAB 仿真，可以分别得到基于模糊阈值和基于固定阈值的航天继电器可靠度退化曲线，如图5 所示。

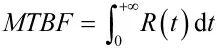
5 结论

本文提出一种基于虚拟样本与模糊阈值的可靠性评估方法，并结合航天继电器的性能退化数据对该方法进行了检验。结果表明，采用本文提出的可靠性评估方法得到的航天继电器125℃下的寿命为137 周，与实际情况相符，能够有效解决小样本、多性能参数产品的可靠性评估问题，对于具有多个性能退化参数装备的维修保障决策提供数据支撑和重要参考。

本文引入模糊概念处理失效阈值的不确定性，其中波动经验系数δ 与隶属函数f（x）是根据产品的历史经验数据由专家综合判断决定的，主观性较大，对评估精度有较大的影响。为了进一步提高评估精度，如何客观、科学地确定波动经验系数δ 与隶属函数f（x）仍需要进行深入研究。