基于落点能量的舰炮制导炮弹对岸射击技术
2020-04-02卢发兴姚鸿鹤
吴 威,卢发兴,吴 玲,姚鸿鹤
(海军工程大学兵器工程学院,武汉 430033)
0 引言
对岸火力支援是舰炮的作战使命任务之一,随着战场环境的复杂化,常规炮弹的射击距离近、命中精度低[1],难以满足对岸上固定目标的精确打击需求。新型舰炮[2]发展迅速,发射炮弹初速高,且初速可控,射击距离远,同时,制导炮弹由于其制导功能,可以显著提高命中精度和毁伤能力。因此,采用新型舰炮发射制导炮弹,能够实现对岸上固定目标的精确打击,具有较大的优势。
当前,国内外均在大力发展舰炮制导炮弹[3],针对制导炮弹的导引控制技术研究较为成熟。见文献[4-12]。可见,国内外文献对于制导炮弹制导律的研究较为深入,但对于初速变化的制导炮弹火控解算问题,没有进行深入的研究。
本文针对新型舰炮初速可调的新特点,开展了制导炮弹对陆固定目标的射击诸元解算技术研究。炮弹在落点具有能量越大,对目标的毁伤越高的特点。为获得对目标最大的毁伤效能,本文以落点能量最优为指标,进行射击诸元解算。通过建立制导炮弹外弹道方程,运用带落角约束的制导律,求解落点能量最优时相应的最优弹丸初速和射角,并得到稳定射击诸元的解算方法,对制导炮弹弹道随射角变化关系、落点能量随初速及射角的变化关系进行了分析。
1 制导炮弹外弹道模型
制导炮弹采用卫星/惯性制导,飞行过程中弹道可划分为主动段和被动段两个阶段。当炮弹离开炮口后,首先进入被动段运动,保持一定时间的零攻角飞行,进行姿态的稳定控制,并进行搜星定位。而后,进入主动段运动,制导炮弹按捕捉到的卫星信号以预先规划好的制导律飞行、攻击目标。
为描述制导炮弹的运动过程,考虑空气动力、重力、科氏力,得到制导炮弹的外弹道模型[13]为:

式中,(x,y,z)为制导炮弹在发射坐标系中的位置,V为炮弹速度,m 为炮弹质量,θ 为弹道倾角,σ 为弹道偏角,Fx、Fy、Fz为制导炮弹空气动力在弹道坐标系上的分量,gx、gy、gz为重力加速度在弹道坐标系上的分量,akx、aky、akz为柯氏加速度在弹道坐标系上的分量。空气动力可通过式(2)进行计算:
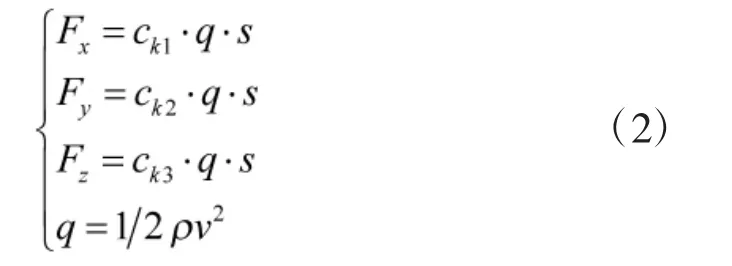
其中,q 为动压,ρ 为制导炮弹当前高度下的空气密度,s 为制导炮弹特征面积,ck1、ck2、ck3为分别轴向力系数、法向力系数、侧向力系数。
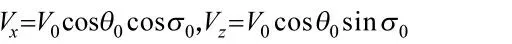
2 基于终端落角约束的制导律
2.1 相对运动方程组
为简化分析,以目标和制导炮弹质心为基准,将制导炮弹的运动解耦成纵向平面和侧向平面两个分量上的运动[14]。其中,纵向平面为制导炮弹质心、目标及地心所确定的平面,侧向平面为过目标和制导炮弹质心且与纵向平面垂直的平面。
首先建立纵向平面内的相对运动方程,如图1所示,r 为制导炮弹与目标之间的相对距离,v 为制导炮弹的速度,ηd为目标高低视线角,θ 为当前时刻的弹道倾角,为制导炮弹速度矢量与弹目视线间的夹角。
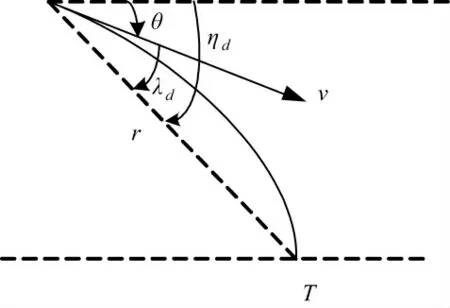
图1 纵向平面内炮弹与目标相对运动关系图
由图1 中的弹目关系可以得到,纵向平面内,目标和制导炮弹之间的相对运动方程为:

在式(4)中,等式两边对时间同时进行求导,可以得到:
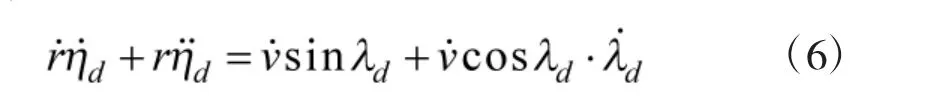
将式(3)~式(5)代入至式(6)中,并进行整理可以得到纵向平面内的相对运动方程为:
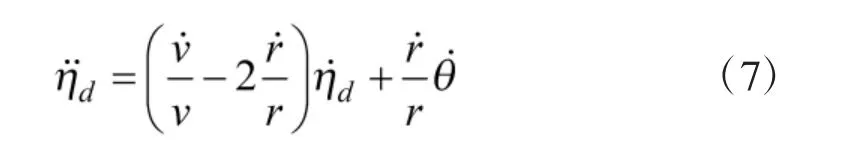

同理可以得到侧向平面内的相对运动方程为:
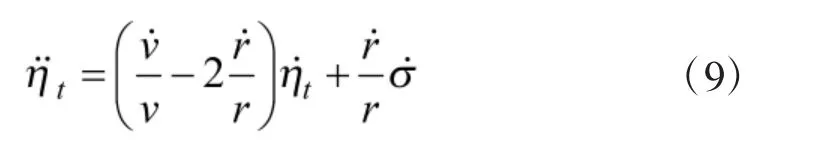
2.2 纵向平面内导引控制规律
为提高对目标的毁伤效能,采用终端落角约束的制导律,以增大制导炮弹的末端落角。首先研究纵向平面内的制导律,以炮弹落角为约束条件,为保证制导炮弹落地时的速度倾角等于要求的落地倾角,视线角终端约束应满足以下两个条件:

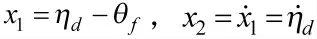
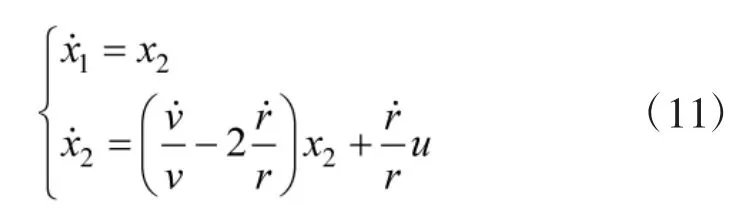
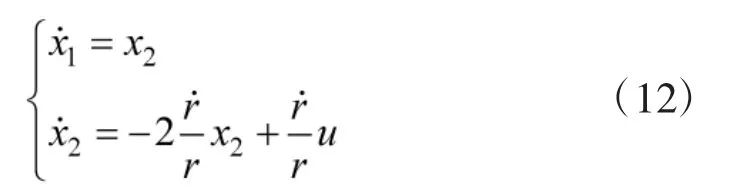

根据式(13)建立系统的二次型性能指标函数[15],并应用极小值原理,可以求解得到带有终端落角约束情况下的法向导引方程:
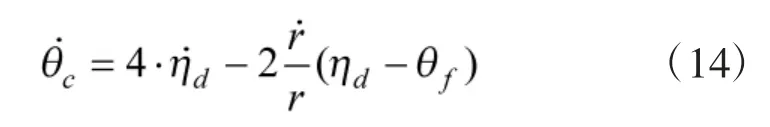
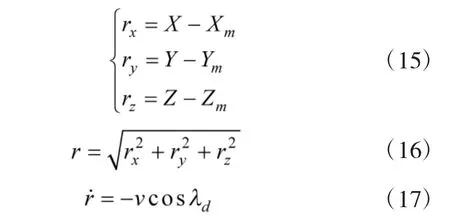
定义Tg 为炮弹剩余飞行时间估算值,则可以得到:

式(14)可以变换为:

其中,视线角速率可以通过以下公式来进行计算:
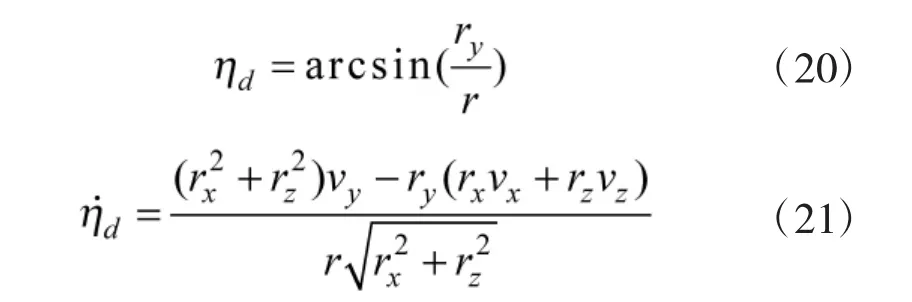
2.3 侧向平面内导引控制规律
一般而言,在命中目标时,仅要求炮弹在落点的落速方向为θf,但对炮弹的进入方向不作要求,因此是自由无约束条件的,仅需满足。类似纵向平面内导引规律的推导过程,取状态变量,可以得到状态方程为:

根据式(22)建立系统的二次型性能指标函数,并应用极小值原理[14],可以求解得到侧向导引方程:

3 基于能量最优的射击诸元解算
3.1 炮弹初速与炮弹射角的解算
由动能定理,可得制导炮弹在落点处具有的能量为:

其中,vf为制导炮弹落点处的速度。
在一定的弹道气象条件下进行射击,炮弹弹道由弹丸初速、射角和弹道系数3 个因素唯一确定[16]。打击岸上固定目标时,使用初速可控舰炮发射制导炮弹,可根据弹丸初速与射角的对应关系,采用上述制导律,实现多种弹道方案对目标的准确命中,如下页图2 所示。
因此,以制导炮弹在落点的能量最优为约束条件,求解得到最优的弹丸初速与射角,从而获取一条唯一的最优弹道。由式(25)可知,当炮弹落点速度最大时,炮弹落点能量最高,因而问题转化为求解落点能量最大时的弹丸初速与射角,基本流程如下:
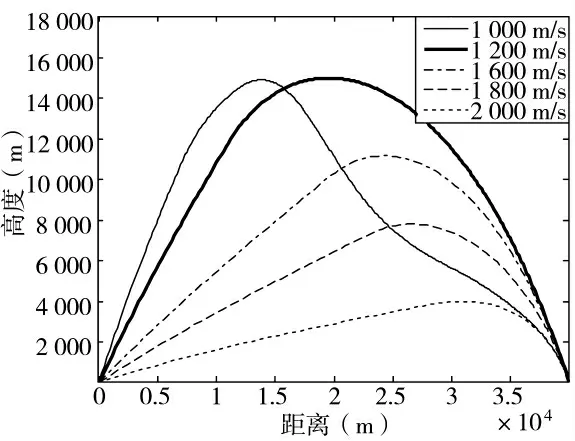
图2 制导炮弹弹道方案示意图
1)初始化参数,主要包括目标信息、终端落角约束角度θf、制导炮弹初速取值范围[V1,V2]及射角取值范围[θ1,θ2];
2)确定制导炮弹初速初值V0_1,射角初值θ0_1,炮弹初速迭代步长,射角迭代步长,制导炮弹实际落点与预设目标距离之间的偏差,制导炮弹实际落角与终端落角约束角度之间的偏差;
3)联合制导炮弹外弹道方程及导引方程,进行弹道解算,由式(25)求解炮弹落点能量E11;
5)重复步骤3)、步骤4)进行迭代计算;
3.2 稳定射击诸元的解算
若初速可控舰炮使用制导炮弹对岸上固定目标进行打击,不同于传统舰炮其射击诸元包含4项,分别为炮弹初速V0、炮弹飞行时间tf、舰炮的稳定方向瞄准角β 和稳定高低瞄准角φ,求解流程如图3 所示。
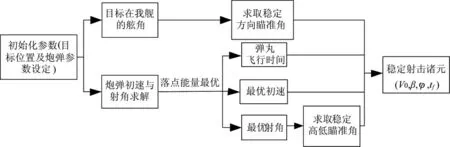
图3 制导炮弹射击诸元求解流程图
由3.1 节可知,以落点能量最优为约束,通过弹道解算与迭代计算,可以求解得到与具有最优落点能量相对应的炮弹飞行时间tf、炮弹初速V0和射角θ0,则舰炮的稳定高低瞄准角φ 及稳定方向瞄准角β 可以通过以下公式进行计算:

其中,Δφ0为舰炮高低零位修正量,Δβ0为舰炮方向零位修正量,Qw为目标方位角。
4 仿真分析

4.1 制导炮弹弹道随射角变化关系
首先研究制导炮弹初速固定时其弹道随射角变化规律,图4 给出了制导炮弹初速为2 000 m/s 时弹道随射角变化规律。
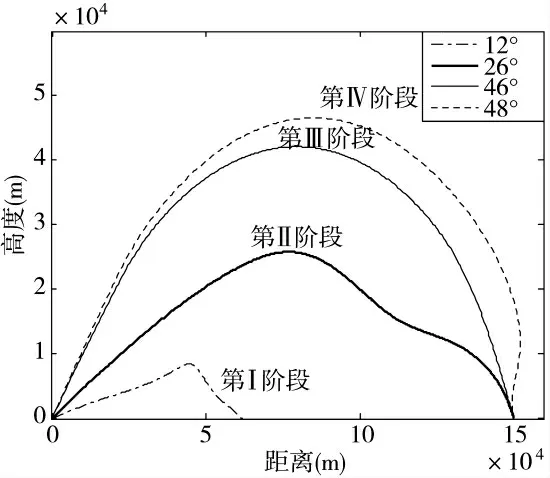
图4 制导炮弹弹道随射角变化规律
如图4 所示,当制导炮弹初速固定时,将弹道随射角变化划分为4 个阶段:
第Ⅰ阶段:当射角小于26°时,随着射角的增加,制导炮弹射击距离逐渐增加,直至制导炮弹通过机动能以约束角度命中目标;
第Ⅱ阶段:制导炮弹均能命中目标,并且随着射角的增加,制导炮弹为命中目标所需要做的机动减小,能量损失随之减小,如图中射角为46°时的弹道,制导炮弹所做的机动最小;
第Ⅲ阶段:随着射角的增加,制导炮弹通过机动能够按照规定的落角约束命中目标,但所需要做的机动逐渐增加,能量损失随之增大,直至不满足命中条件,此时射角为48°。
第Ⅳ阶段:当射角大于48°时,随着射角的增加,制导炮弹通过机动无法满足落角约束条件及射击距离要求。
因此,当制导炮弹弹道由第Ⅱ阶段向第Ⅲ阶段变化时,即射角为46°时,制导炮弹的机动最小。此时,制导炮弹飞行过程中由于机动而损失的能量最小,落点能量最高,所对应的射角为当前初速下的最优射角,所对应的弹道为当前初速下的最优弹道。
4.2 落点能量随初速及射角的变化关系
对不同炮弹初速条件下,炮弹落点能量随射角的变化关系进行研究,如图5 所示。
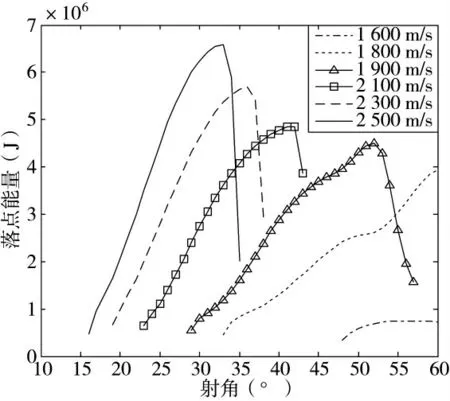
图5 落点能量随射角变化关系图
由图5 可知,对于岸上某固定目标进行打击时:
1)初速固定时,当射角过小或者过大,即弹道变化处于第Ⅰ阶段和第Ⅳ阶段,制导炮弹通过机动不能满足射击距离和落角约束条件;
2)当初速为1 600 m/s 时,制导炮弹弹道随射角变化经历Ⅰ、Ⅱ、Ⅲ阶段,落点能量随射角的增大先增加后减小;
3)当初速为1 800 m/s 时,制导炮弹弹道随射角变化经历Ⅰ、Ⅱ阶段,落点能量随射角的增大逐渐增加;
4)当初速大于1 800 m/s 时,制导炮弹弹道随射角变化经历Ⅰ、Ⅱ、Ⅲ、Ⅳ4 个阶段的变化,落点能量随射角的增大先增加后减小;
5)炮弹初速越高,最优落点能量越大,所对应的射角越小。
4.3 舰炮制导炮弹射击诸元解算
对150 km 处固定目标进行打击,结合4.1 节与4.2 节分析,在不同初速条件下,基于落点能量最优得到制导炮弹的射角,表1 给出了不同初速时基于能量最优所求得的制导炮弹弹道数据。
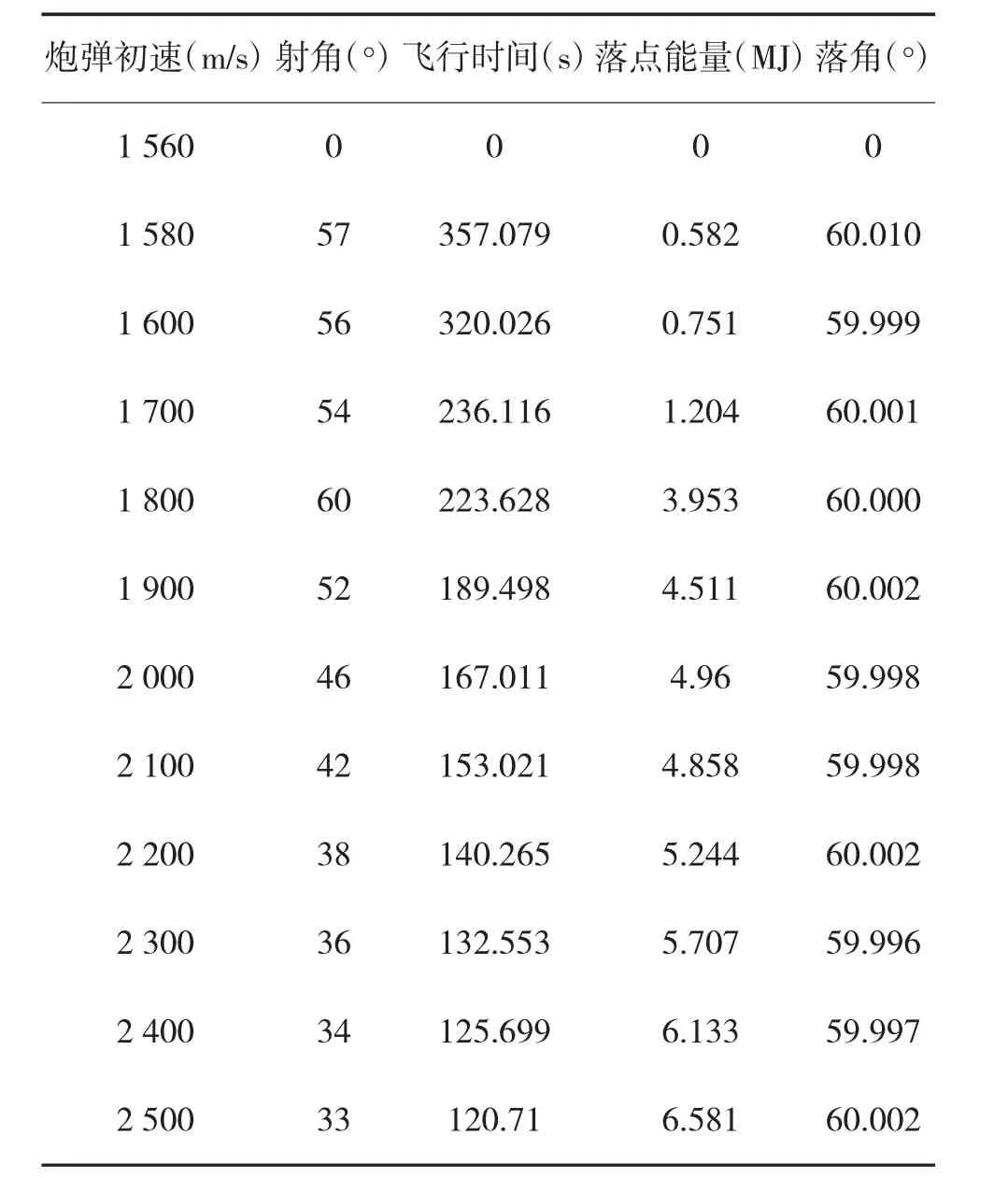
表1 制导炮弹弹道数据
由表1 可知,当初速小于1 580 m/s 时,受到射击距离与落角约束的限制,制导炮弹通过机动无法命中目标;当初速大于1 580 m/s 时,落点能量随弹丸初速的增加而增加,弹丸飞行时间减小;当初速为2 500 m/s 时,制导炮弹的落点能量最大。基于能量最优的方法,根据计算得到的弹道数值即可求解得到当前距离下的稳定射击诸元(V0,β,φ,tf),如表2 所示。
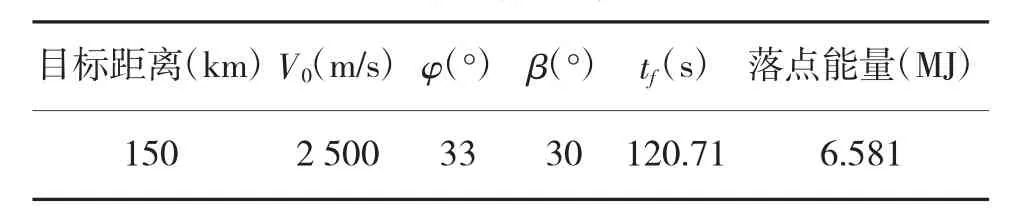
表2 射击诸元解算结果
5 结论
根据新型舰炮初速可控的特点,本文基于能量最优的方法提出了制导炮弹对岸射击的射击诸元求解思路,为制导炮弹火控解算提供了理论参考,对于新型舰炮制导炮弹诸元解算和射表制定等实际应用具有重要意义。
