基于KPCA和模糊物元模型的公交运营质量综合评价
2020-04-01韦兰辉靳文舟
韦兰辉, 靳文舟
(华南理工大学土木与交通学院,广州 510000)
城市公共交通在整个交通运输系统中占相当大的比重,它联结社会的各个要素,保障着城市居民的日常生活,承担着大量的市内乘客运输任务,对城市建设和发展来说至关重要[1]. 而常规公交系统灵活性好、适应性高、承载量大,已经在各个国家和地区深入人心. 为了将“公交优先”的观念继续向前推进,必须对其开展深入研究,对其服务质量开展系统深入的评价,为提升公交市场活力提供实践基础和研讨方法,从而不断提升其服务质量[2-3].
经典的公交评价方法有层次分析法[4]、神经网络法[5]和模糊评价法[6]等,但是它们对于得到的评价结果略有不足. 比如神经网络法需要的数据量庞大,并对算法参数有着严格限制;层次分析法则过于主观,客观性不足. 在公交运营评价指标方面,有使用满意度调查法和集对分析法来对指标体系进行综合评价[7]. 服务质量评价方面,有以公交运行服务质量评价的系统边界,以价值、能耗与信息为基本维度来进行构架,还有以乘客感知和期望之差为基本依据来建立公交服务质量评价体系[8-9].
综上所述,目前已有很多学者从不同角度选取了多种指标来构建城市公交服务质量模型,并在此基础上采用多种方法对线路进行评价,但鲜有就某一条线路请乘客作为评价专家,将乘客感知作为切入点来构建该线路的公交质量评价体系. 针对以上问题,本文拟将KPCA[10]和模糊物元法[11]相结合对公交线路进行运营质量评估,以充分利用KPCA对指标降维效果显著[12-14]和模糊物元法适用于模糊集合分析的特点[15].
1 评价指标体系设计
1.1 公交线路运营质量评价指标体系
确立公交线路运营质量评价模型的首要环节是构建科学合理的评价指标体系,通过监测和分析相关指标反映线路的运营水平. 根据《汕尾市城区公交企业服务质量考核暂行办法》,以如下原则构建评价指标体系[16-18]:
1)对地面公交选取的评价指标可以通过观察、统计、评议等方式获得定量或定性的数据值.
2)坚持科学性与操作性兼具,考评内容的确定和指标的选取,应遵循科学合理的原则,与考核实际相吻合,并能全面反映公交运营状况.
3)评价指标应采用定性与定量相结合的方式,除了定量数据获取外,还应全方位充分体现乘客的感受.
4)对于企业应设置正向激励指标,激励企业进行积极改善,提高社会满意度.
依据上述原则和汕尾公交企业服务质量考核办法,确定公交线路运营质量评价指标体系,如表1 所示. 其中,一级指标包含运营服务、服务管理、安全管理和社会评价4 项.该指标体系利用9 个二级指标和18 个三级指标合理地体现公交线路的运营水平和管理水平,对线路的运营水平评价具有重要影响的因素.

表1 公交线路运营质量指标体系Tab.1 Quality index system of bus line operation
1.2 指标分级标准
根据各指标值的历史数据和专家意见,对各个指标进行等级划分及取值范围规定. 公交线路运营质量评价指标分级标准如表2所示,其中规范驾驶、车辆整洁、乘客满意度均由德尔菲法决定,根据行业专家打分情况取均值,作为定性指标的最终指标值. 在进行计算时将百万车公里死亡率、运营违章、政府奖惩和市民媒体投诉次数等经过数据处理后得到相应的响应级别数值. 其余指标本文以在汕尾进行的《汕尾市城区公共交通专项规划》和《汕尾市城区公交企业服务质量考核暂行办法》调研所采集的数据进行分析.
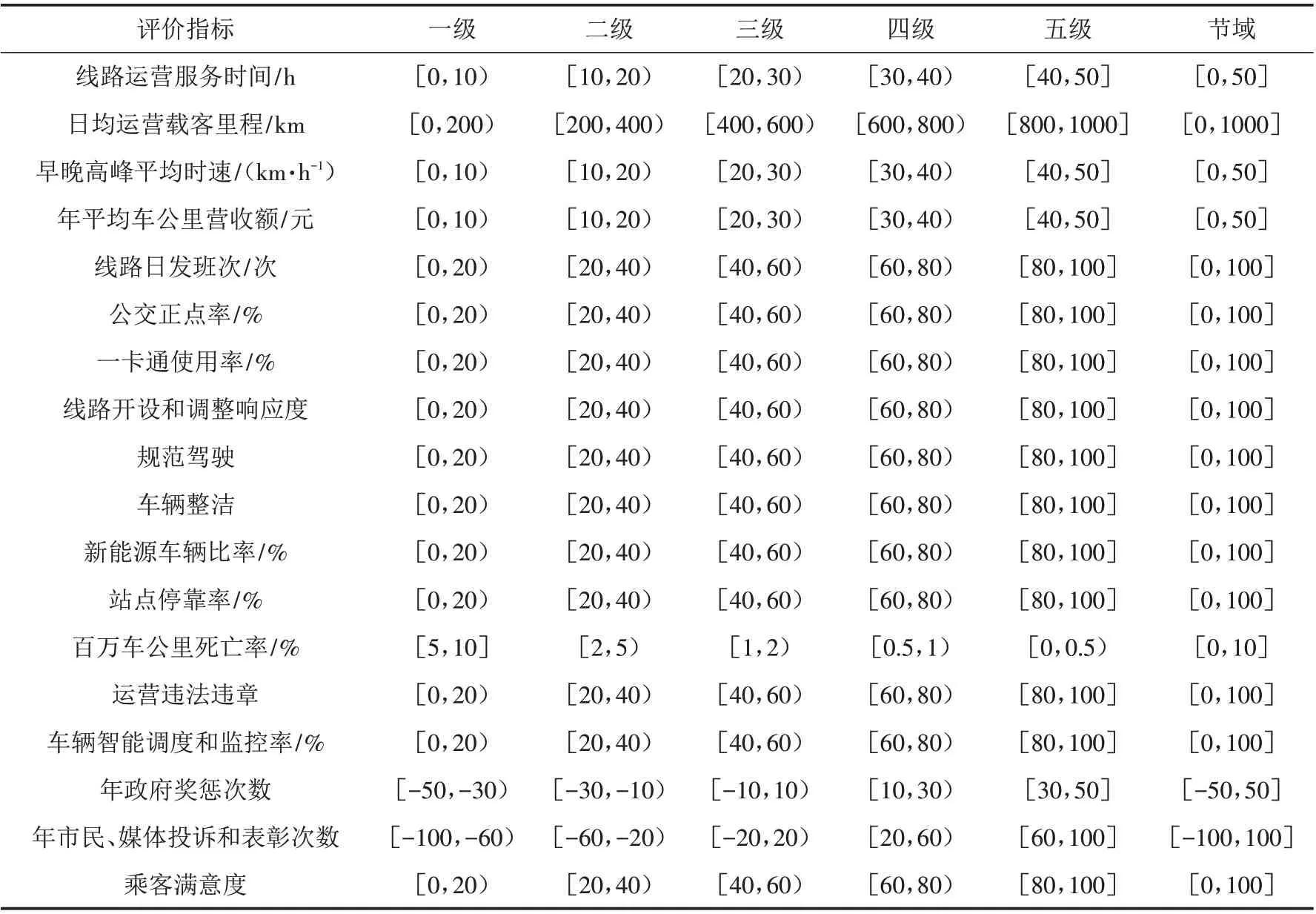
表2 公交线路运营质量指标分级Tab.2 Classification of bus line operation quality indicators
2 公交运营质量综合评价模型
2.1 核主成分分析法
核主成分分析(Kernel Principal Components Analysis,KPCA)是一种非线性推广的主成分分析. 由于在非线性统计和高阶统计特征提取上具有较好的效果,相对于传统的主成分分析观测数据的特点,具有更好的评价能力. 通过变换将原有空间变换到高维空间,使得非线性关系在高维空间变为线性,再对高维空间的数据进行PCA变换[19]. 核主成分分析方法能将综合指标的贡献率进行高度集中,利用少数的综合指标实现公交线路运营质量的评价.
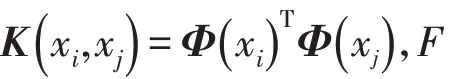
在映射后的RF空间中,样本去均值化后的协方差矩阵:
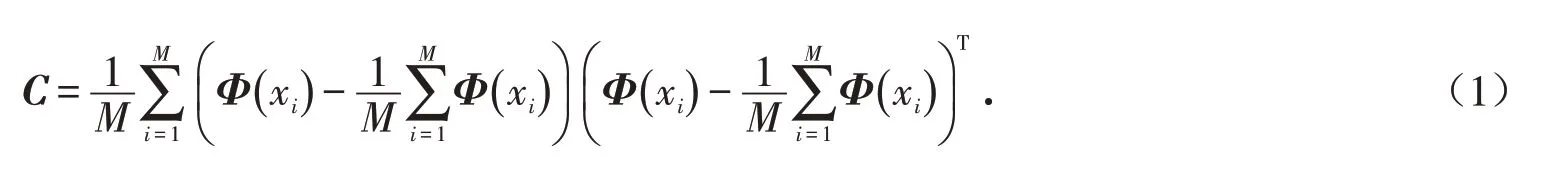

由式子Cv=λv 求出C 的特征值λ,v 是对应λ 的特征向量. 把(2)式带入此式子中得到:

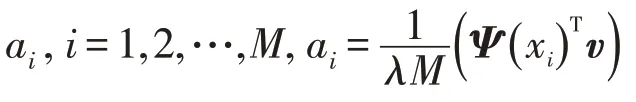

这样我们便得到C 的特征向量的性质,即是{Ψ ( x1) ,Ψ( x2),…,Ψ( xM)}张成的.
因为Cv=λv,所以(Ψ ( xk))TCv=λ(Ψ ( xk))Tv . 把(4)式带入得
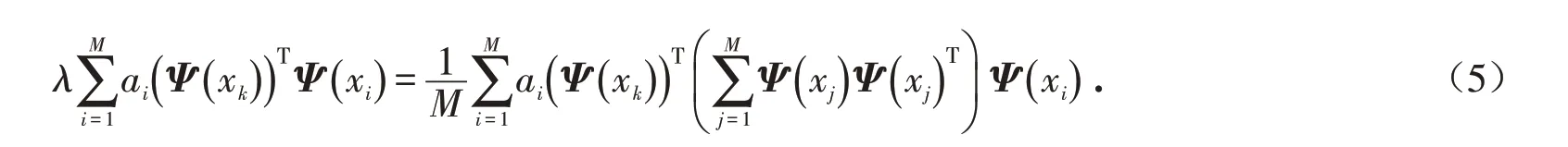
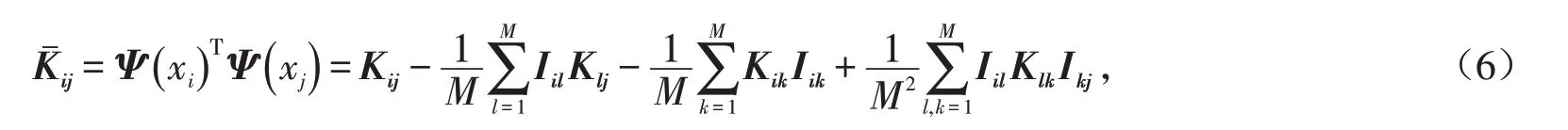
其中:Kij=Φ( xi)TΦ( xj),K 为核矩阵,所以:
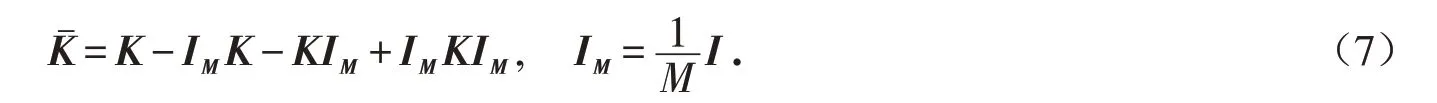

应用核主成分分析方法进行坐标投影变换,突破指标间线性相关与非线性相关关系的限制,过程更为简便,同时降维作用更加明显. 另外,采用核主成分分析算法,能使多类指标共同参与计算,得到的评价结果更加全面、真实可靠.
2.2 模糊物元模型
模糊物元模型是模糊集合理论应用于物元模型中,模糊集合用隶属度函数来进行描述,物元可拓模型被广泛地应用于各行业的决策[20]. 给定评价对象的名称为N,它关于特征指标C 的量值为V,以有序三元R=( N,C,V )作为描述事物的物元[21]. 当V具有模糊性时我们称R为模糊物元,记作Ro=( No,Cm,Vm),Vm为事物No的特征指标Cm取值Vom时的模糊量值. 模糊物元分析模型基本分析步骤如下:
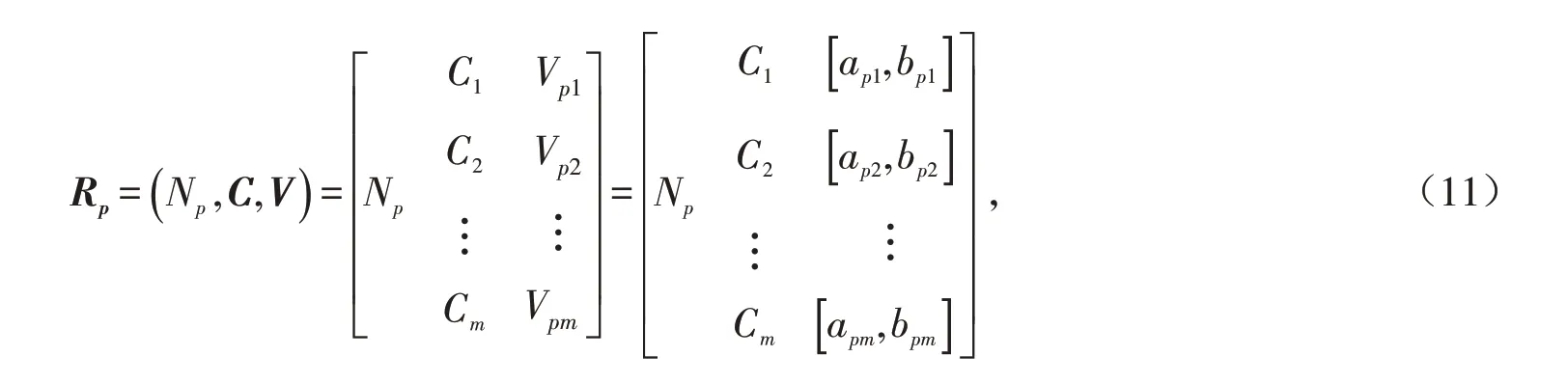
1)确定物元矩阵
设事物N有m个特征指标C1,C2,C3,C4,…,Cm,相应的量值分别为Vom,R为m维模糊物元. 其中N为评价样本,C为评价指标,
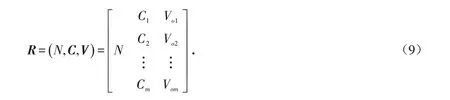
2)确定经典域
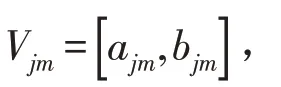

其中:Nj表示所划分的j 个等级;Cm表示等级Nj的特征;ajm为评价等级j 数据范围的下限,bjm为评价等级j 数据范围的上限.
3)确定节域
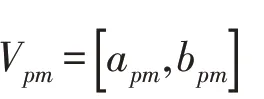
其中:Np表示评价等级的全体;apm为评价等级数据范围的下限;bpm为评价等级数据范围的上限.
4)物元数据模糊化处理
评价指标根据其特点分为越大越优型和越小越优型,在进行数据模糊化的时候要分类考虑. 如公交正点率为越大越优型指标,百万车公里死亡率为越小越优型指标,这两个指标应选用下列公式进行数据模糊化.

其中:Vi是指标的实测值;Vm为模糊化处理后的数值;a 为该指标的下限值;b 为该指标的上限值. 两式分别为越小越优型指标和越大越优型指标.
5)确定待评价模糊物元
对于待评价公交线路,把所得到的数据结果用物元表示有:
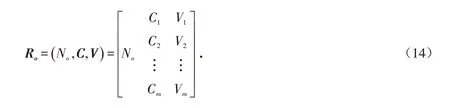
将其称为公交线路的待评物元,No表示待评公交线路. Vm表示No关于Cm的量值,即实际数值经过模糊化后的数值.
6)计算待评价线路关于各等级的关联度
确定关联度函数为Kj( )Vm,关联函数表示物元的量值取为实轴上一点Vm时,物元符合要求的取值范围程度. 关联函数为:
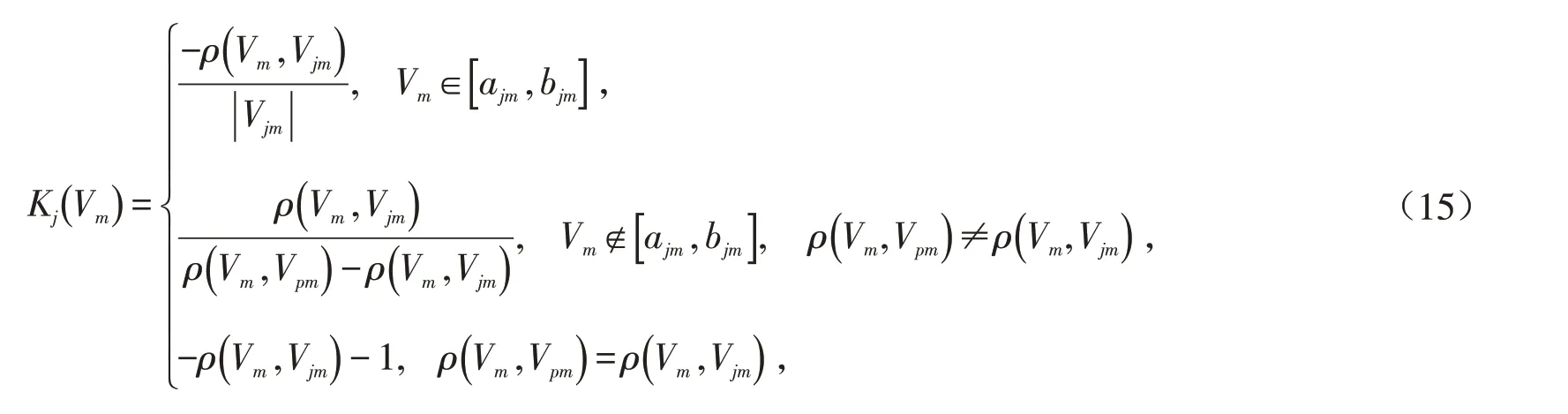
其中:|Vjm|= |bjm-ajm|为区间Vjm=[ajm,bjm]的模;ρ(Vm,Vjm)为实轴上任意点Vm到区间Vjm的距离;ρ(Vm,Vpm)
定义为实轴上任意点Vm到区间Vpm的距离;bpm和apm分别为指标属性值的取值上限和下限.
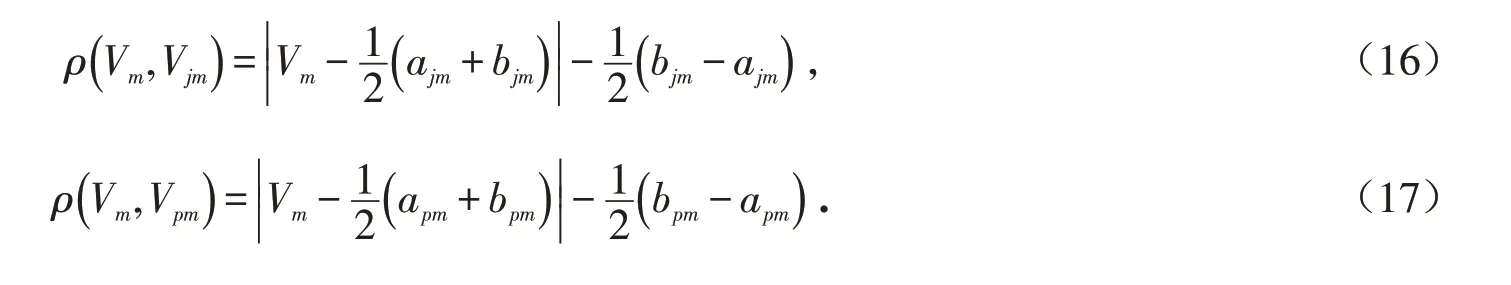
令ωm为各评价指标Cm的权重,则有:

称Kj( No)为待评价公交线路No关于等级j 的关联度.
7)计算公交线路综合评价结果
将经过加权计算后的关联度Kj( No)进行比较,最大值所对应的级别即为该公交线路的运营质量水平.令Kjo=max{Kj( No)},则待评价公交线路No属于等级jo.
2.3 KPCA和模糊物元公交线路运营质量评价模型
KPCA和模糊物元模型利用核主成分分析法(KPCA)对指标进行降维处理,并应用模糊物元模型分析公交线路的运营质量水平. 本文应用此模型评价公交线路的流程如图1所示.

图1 公交线路运营质量评价流程图Fig.1 Evaluation flowchart of bus line operation quality
3 汕尾市公交线路运营质量分析
本文以在汕尾进行的《汕尾市城区公共交通专项规划》和《汕尾市城区公交企业服务质量考核暂行办法》项目中调研所采集的原始数据经处理后进行分析. 选取其中具有代表性的12条线路进行分析,为保证模型的普适性,12条线路中包含不同公交企业运营的线路. 经符合经典域处理后的数据如表3所示.
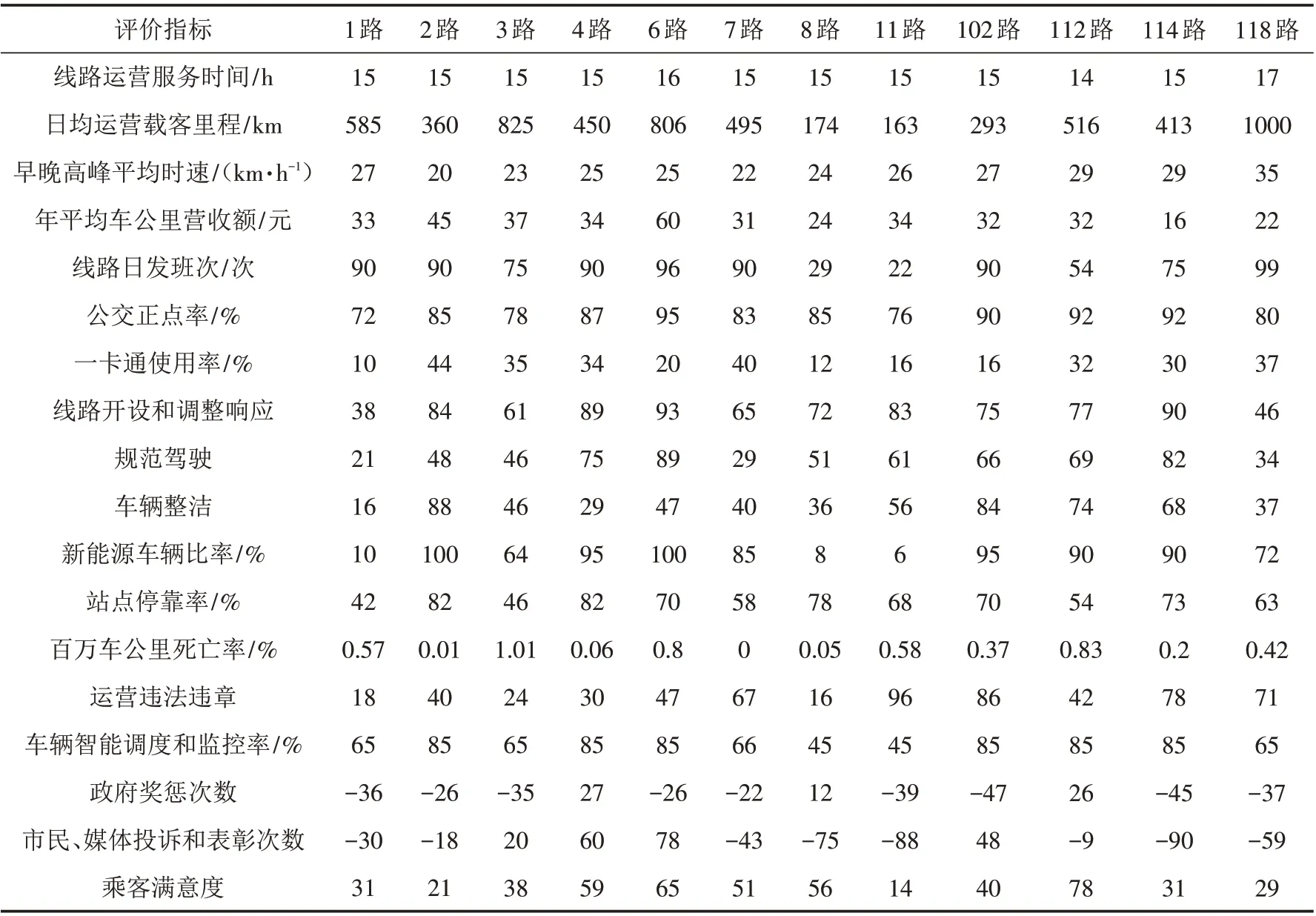
表3 汕尾市公交线路评价指标值Tab.3 Evaluation indexes of bus routes in Shanwei
3.1 核主成分分析法处理
鉴于KPCA核函数具有泛化性能弱、学习能力强及降维效果明显的特点,通过以上模型构建思想,可有以下数据处理步骤.
Step1:输入表3数据并进行标准化预处理.
Step3:中心化矩阵并进行特征值分解,特征值按降序排列.
Step4:用下式分别计算各特征值的贡献率rate 及累计贡献率sumrate .
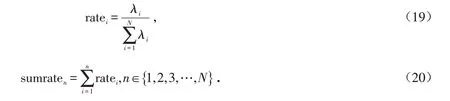
Step5:选取具有代表性的主元,并将其对应的贡献率数据标准化处理后作为模糊物元模型中采用的指标权重.
使用MATLAB编译核主成分分析法,对数据进行有效的非线性特征提取,取前5个特征值组成的P矩阵.所得结果见表4(去除不具代表性数据). 选择前5 个非线性主成分即可代表原始18 个评价指标体系来对公交线路运营质量进行综合评价,将其对应的贡献率经归一化化处理后的数值即为对应综合指标权重,其特征值序号及指标权重ωm为1:0.596 005 967;2:0.292 311 214;3:0.062 877 221;6:0.028 414 865;5:0.020 390 732.
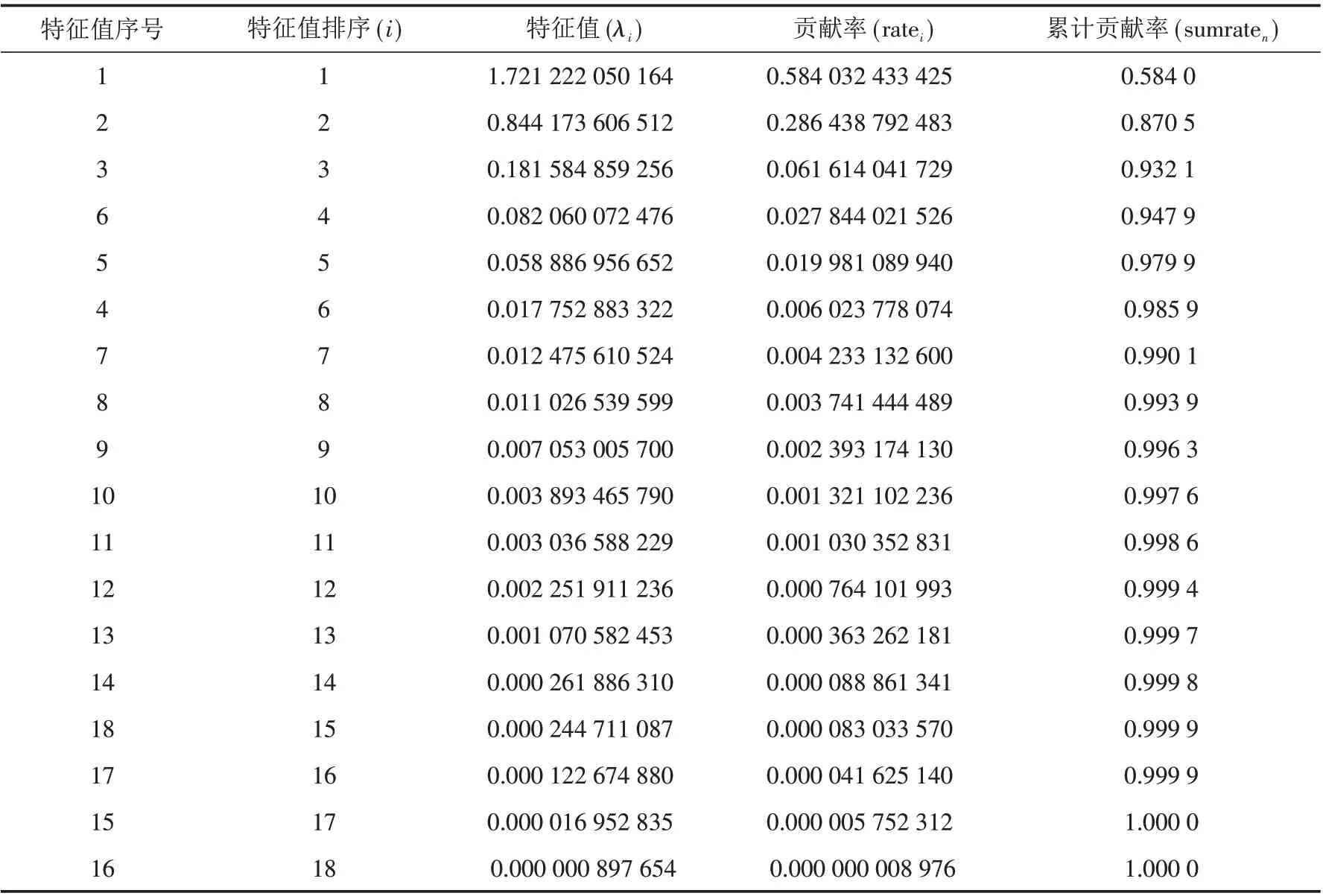
表4 核主成分分析法数据处理结果Tab.4 Kernel principal component analysis data processing results
3.2 模糊物元法评价
将核主成分分析法计算出的综合指标及其权重应用于模糊物元模型当中,计算各公交线路综合评价等级的关联度,如表5所示. 汕尾市公交线路运营质量综合评价物元,由评价等级一级、二级、三级、四级和五级构成的经典域,如表2所示.
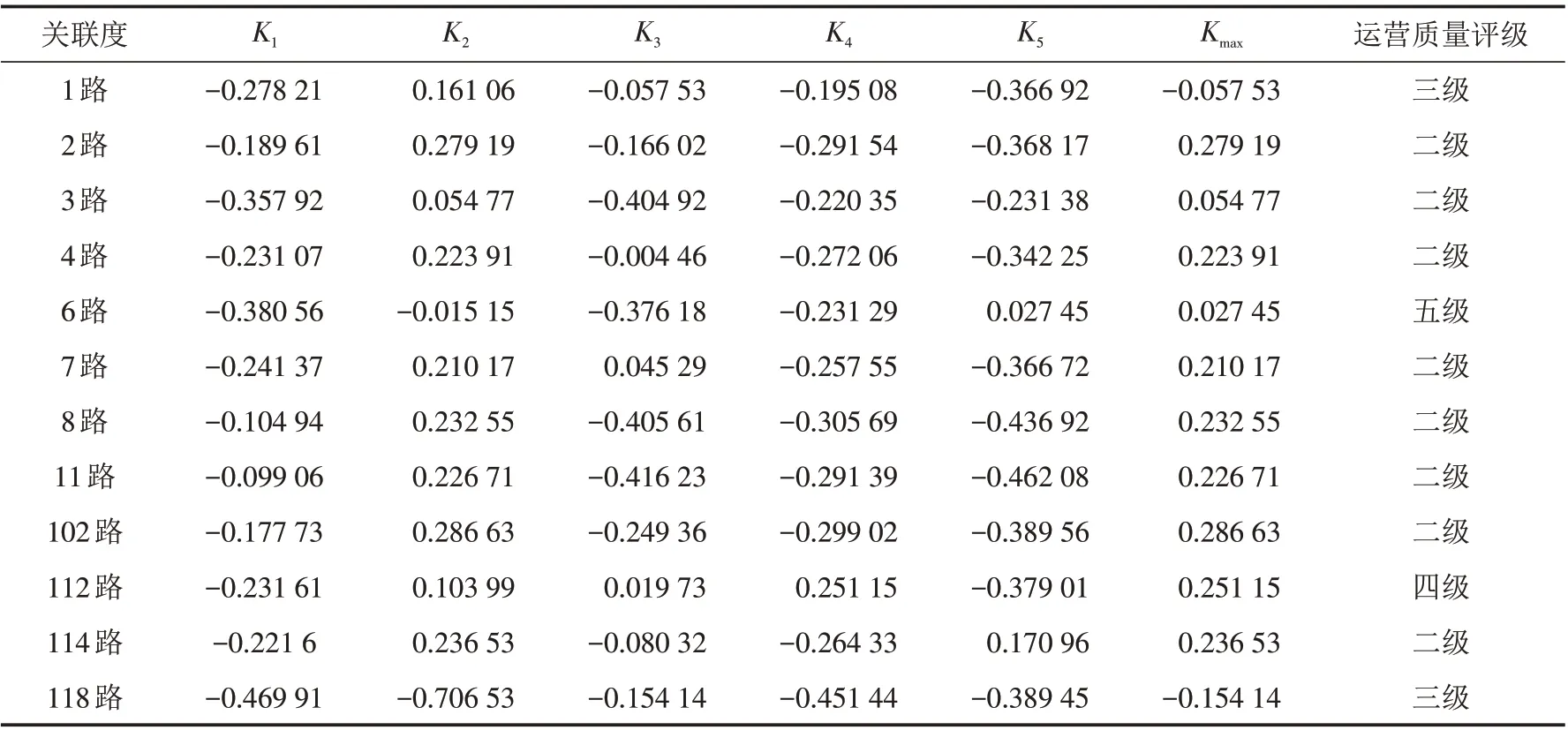
表5 公交线路综合评价等级关联度表Tab.5 Correlation degree table for comprehensive evaluation of bus routes
通过综合评价表5的结果可知,6路公交车的运营质量综合水平对五级的隶属度高,为0.027 45;112路对四级的隶属度高,为0.251 15;1路和118路对三级的隶属度高,分别为-0.057 53,-0.154 14;其余线路均为二级. 因此,在评价的12条线路中,6路的运营质量评价等级最高,属于五级;112路的评价等级排第二;1路和118路评价等级排第三. 评价结果显示公交运营服务质量等级与居民实际感受呈一致性,并且能规避一定的主观映像,如118路的运营时间和班次是最大的,但其奖惩表现较差,则没有评为最高级.
结合汕尾市公共交通发展实际,本文构建的公交线路综合评价模型从影响运营服务质量的主要因素出发,能够比较准确地反应实际公交运营过程中产生的问题,具有较高的准确性,对汕尾市城区公交企业服务质量考核提供一定的依据. 并表明,大量的公交运营服务、服务管理、安全管理和社会评价等指标数据经过核主成分分析法降维处理后,能得到有效的综合指标来应用于模糊物元模型,剔除了对评价结果影响小的指标,简化公交运营质量评价方法.
4 结论
本文将核主成分分析法和模糊物元法结合起来,构建了公交线路运营质量综合评价模型,从运营服务、服务管理、安全管理和社会评价4个方面(18个三级指标)应用模型对汕尾市12条公交线路的运营质量水平进行评价,克服传统评价方法对所有实测样本过度依赖的弊端. 公交线路运营质量综合评价模型所得结果与现实感受情况基本一致,说明该模型具有较高的可靠性及可操作性,可以确定公交线路的运营基本情况,线路的评价等级为公交服务质量考核提供参考,还有助于找出公交线路各层面的优缺点,为提高服务质量提供依据.
