中国石油产业定价市场化进程：基于GARCH与MS-GARCH预测能力的研究

高新新， 王 璐， 李丽虹， 马元慧

（西南交通大学数学学院，成都 610031）

石油作为当今重要的战略资源，对世界各国的经济发展有重大影响. 我国作为石油进口大国，要在第一时间了解石油价格走势情况，研究石油市场波动可以帮助政府决策者采取及时有效的措施. 自从我国石油价格与国际石油价格接轨以后，国际石油市场的变动直接影响到我国的石油市场，对我国的经济产生冲击.因此，研究市场化条件下中国石油市场波动特征及其预测，对于探究未来石油经济发展趋势有重要意义［1］.

我国自1955年开始实行石油定价机制，纵观这大半个世纪以来石油价格形成机制的发展历程，大致可分为“计划定价—计划与市场双轨定价—与国际接轨”三个发展阶段［2］. 从1955年到1981年，在计划经济体制背景下，石油定价及价格调整都由政府决定，而政府在定价过程中几乎不考虑国际市场的影响. 1981年中央政府开始采用“双轨制”，石油定价机制进入了计划与市场双轨并行的阶段，市场因素的加入刺激了石油产业的发展. 1998年的《原油成品油价格改革方案》对石油产业具有重要意义. 此次改革改变了过去由政府定价的单一模式，通过原油与国际原油价格挂钩联动的方式来实现国内石油价格与国际市场接轨. 从1998年至今，国家对石油价格机制进行了多次大大小小的改革，本文选取了几次比较重要的改革. 2001年底进行的改革是此前几次改革中力度最大的一次，从紧跟新加坡市场价格变为与纽约、鹿特丹、新加坡三地市场接轨. 2008年12月，国务院出台关于成品油价格和税费改革的通知，目的在于理顺成品油和原油的价格关系，形成国内成品油价格与国际市场原油价格有控制地间接接轨的定价机制. 2013年3月国家发改委再次对价格形成机制进行调整，对定价机制的主要内容进一步完善. 本文选取这三次改革时间为数据分段依据，主要研究在近二十年与国际接轨阶段中，随着市场化程度的不断增加，石油价格也呈现出不同特征.

国外对于石油的研究起步较早，1931 年Hotelling 提出的可耗竭资源理论是首个研究石油价格的理论.1986年Bollerslev［3］提出广义自回归条件异方差模型即GARCH模型，此后有许多学者开始基于GARCH模型进行石油价格波动的研究，Sharma［4］通过GARCH模型对油价进行预测，Agnolucci［5］比较了GARCH型模型和隐含波动率模型对WTI原油价格的预测能力. Cheong［6］认为GARCH模型对布伦特原油价格波动的拟合效果更好一些，Hou&Suardi［7］采用非参数GARCH模型对石油价格波动进行分析，为学者提供了另一个研究方向. 国内的石油价格波动研究起步较晚，21世纪初关于石油价格的研究才逐渐丰富起来，冯春山［8］发现国际石油价格具有比较明显的ARCH效应，潘慧峰［9］通过ARCH模型对国内石油价格波动进行分析，邹艳芬［10］基于GARCH模型对国际石油价格变动模拟，袁霓［11］应用ARCH类模型对我国大庆石油价格波动率进行研究，发现我价格收益率序列表现出明显的GARCH效应，胡爱梅、王书平［12］认为从短期预测与长期预测两个角度总体来看GARCH 模型要优于ARIMA 模型.

Hamilton［13］提出马尔科夫状态转换（MS）模型，之后该模型被广泛应用于金融时间序列分析，Hamilton&Susmel［14］将MS引入到ARCH模型中，此后许多学者又推广到GARCH模型中. 在国外研究的基础上，国内大多将MS-GARCH模型［15］应用到股票、期货及汇率市场，如孙金丽［16］、吴诣民［17］、华仁海［18］等. 国内鲜少有人将马尔科夫转换机制应用到石油市场并通过此来研究石油产业定价市场化进程.

综上，本文对以下几个方面进行扩展：①基于我国石油定价机制演变背景，除了采用传统的GARCH 模型对大庆石油数据进行拟合及预测，同时也从马尔科夫状态转换的角度进一步研究了石油价格的波动特征，通过对GARCH与MS-GARCH两种模型预测效果的比较来说明在市场逐渐开放的过程中石油价格波动开始出现高低两状态趋势. ②从2001年底的石油定价政策改革迄今为止，我们发现政策变化对石油价格波动预测影响的显著性. 本文将2002年至2018年的数据依据两次重要政策调整时间分为三段，分别对三段数据结合模型进行深入分析，探究政策变化对石油价格波动的影响.

1 模型

1.1 GARCH模型

GARCH 模型是在金融时间序列分析中运用较为广泛的波动率模型. 本文用到的是比较常见的GARCH（1，1）模型，具体形式为方程（1）～（3）：

其中：μt是条件均值；ht是条件方差；εt是残差扰动项，{et} 是一个白噪声过程，ω 是常数项，α 和β 分别是ARCH 项和GARCH 项的系数. GARCH 模型有两个约束条件：①参数非负：ω ＞0；α,β ≥0. ②参数有界：α+β ＜1. 这两个条件是为了确保非负性和平稳性.

1.2 MS-GARCH模型

MS-GARCH模型是在GARCH模型中引入了马尔科夫状态转移变量，见方程（4）～（6）：

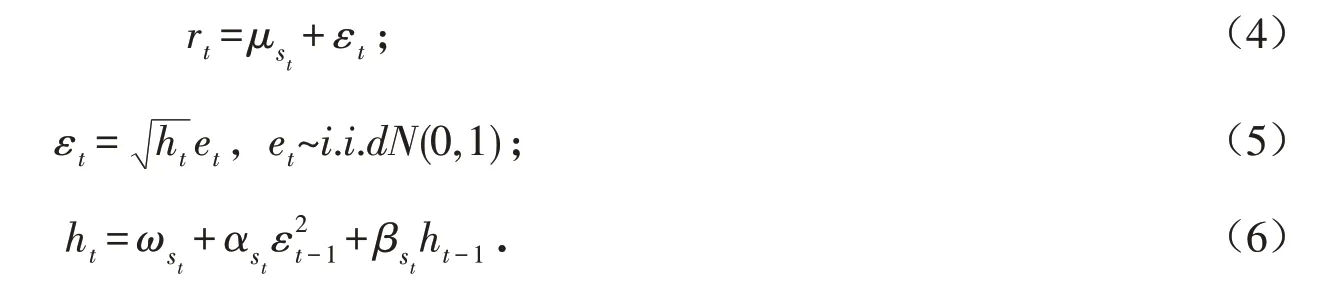
式中：参数μst,ωst,αst,βst依赖于t 时刻的状态变量st，本文考虑st=1和st=2 两种状态. 两种状态之间的转移服从离散的马尔科夫过程，即

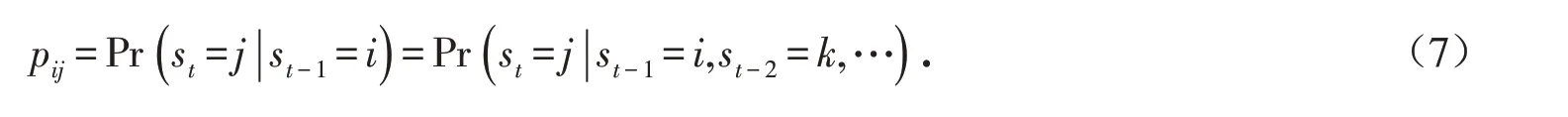
其中状态转移矩阵为

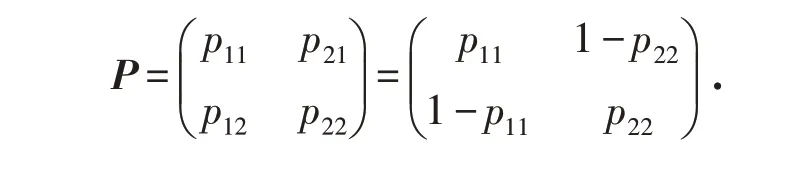
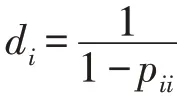
对于MS-GARCH模型我们依然采用极大似然法来估计参数. 类似GARCH模型我们可以得到对数似然函数：

但是函数中状态变量st未知，因此我们引入

其中参数集θ={ μ0,ω0,α0,β0,μ1,ω1,α1,β1,p11,p22}，此时有

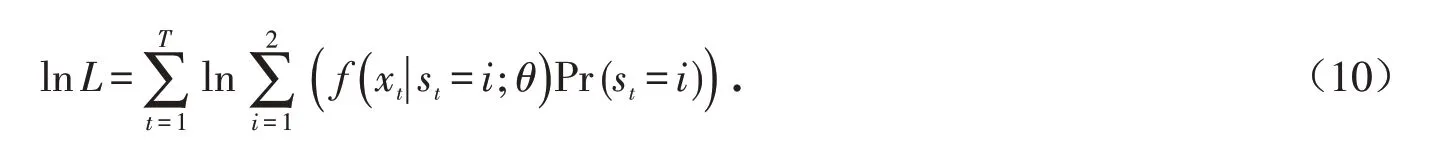
最后可以通过Hamilton［19］的滤波过程和Kim［20］的平滑算法结合极大似然估计法来求得参数值.

2 实证

2.1 数据及基本统计特征

原油和成品油同是中国石油产业的重要组成部分，鉴于二者之间密不可分的联动关系，本文选取中国大庆原油日度现货价格数据. 样本期间为2002年1月2日至2018年11月30日，共计4156个数据，来源于Wind财经.

首先对选取的数据按照引言中的三次改革时间进行分段（表1）.

表1 样本分段设定Tab.1 Sample segmentation setting

其次，将价格数据转化为日收益率，计算公式为：

式中：Pt和Pt-1分别表示当期和滞后一期的原油价格.

每一段时间的原油价格走势图、收益率走势图和收益率的描述性统计量结果如图1和图2所示. 可以发现，在第一段和第三段时期中原油价格分别有一次大幅度下跌，我们认为是由于2008年金融危机和2016年国际油价暴跌所导致的.

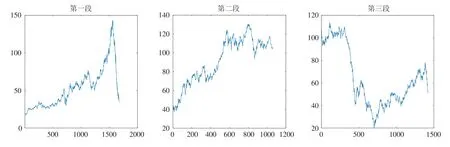
图1 大庆原油价格走势图Fig.1 Trend charts of Daqing crude oil prices

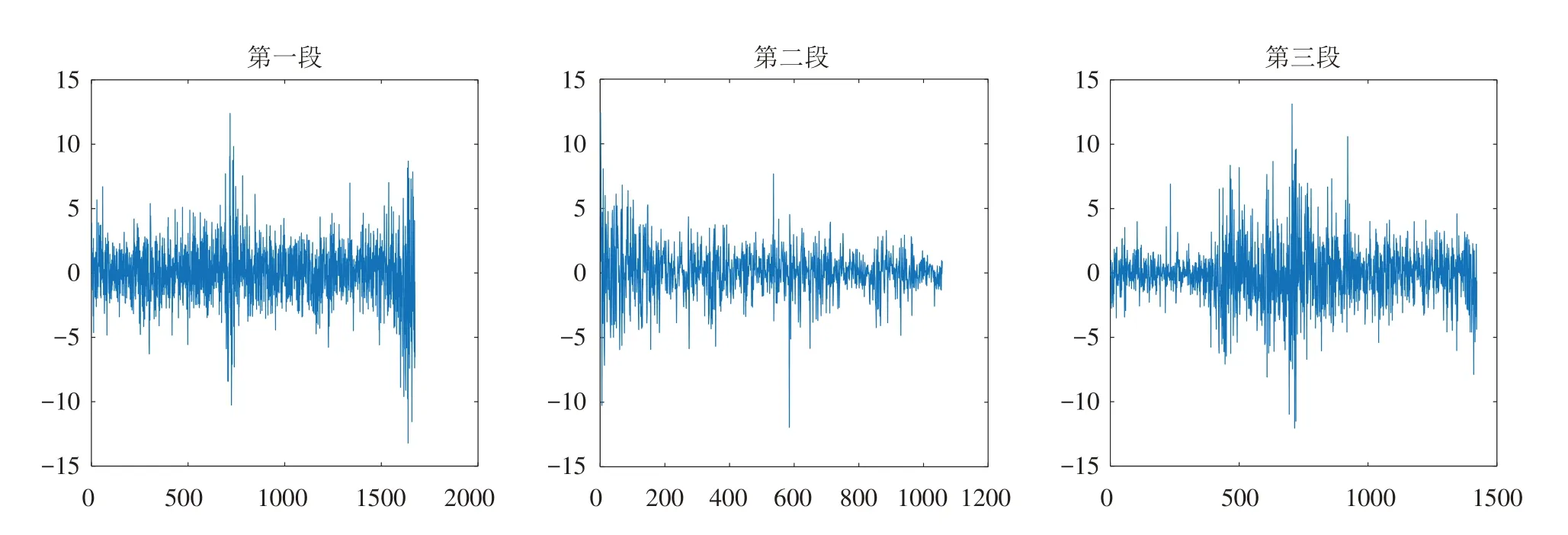
图2 大庆原油收益率走势图Fig.2 Trend charts of Daqing crude oil returns

表2 结果显示，第一段和第二段时期收益率序列的偏度小于0，说明序列呈现出左偏态，而第三段稍右偏. 三段时期的峰度都大于3，说明序列相对于标准正态分布为尖峰分布. J-B统计量值较大，说明拒绝序列服从正态分布的零假设. 因此，这三段时期的序列具有尖峰特征且不服从正态分布，这说明我们选择GARCH模型来进行拟合是合理的.

表2 收益率的描述性统计量Tab.2 Descriptive statistics of returns

2.2 参数估计结果

对这三段数据分别用GARCH模型和MS-GARCH模型拟合参数，其结果见表3. MS-GARCH模型中两种状态的均值有所不同，说明波动状态确实存在两种情况. 通过对数极大似然值LLN与AIC值，不难发现，在样本估计中MS-GARCH模型比GARCH模型有一定的优势.

图3和图4分别描绘了每一段时期的波动率和平滑概率，其中左图表示状态1，右图表示状态2. 当某种状态下的平滑概率大于0.5时，表明仍处于该状态，并未发生状态转移. 根据以上图表，分析结果如下：

1）在对参数估计结果分析时已说明条件方差存在两种状态，根据图3和表4，我们定义st=1为低波动率状态，st=2 为高波动率状态. 表4中的转移概率值均小于1说明没有一种状态是完全稳固的，只是在各自的转移状态中相对而言比较稳定.

2）三个时期中的低波动状态的转移概率p11都大于0.9，说明大庆石油价格在低波动状态时，下一时刻依然处于低波动状态的概率较大，而转移到高波动状态的概率很小，即低波动状态的持续性较强. 图3和图4中左侧图像也可以印证这一结论.

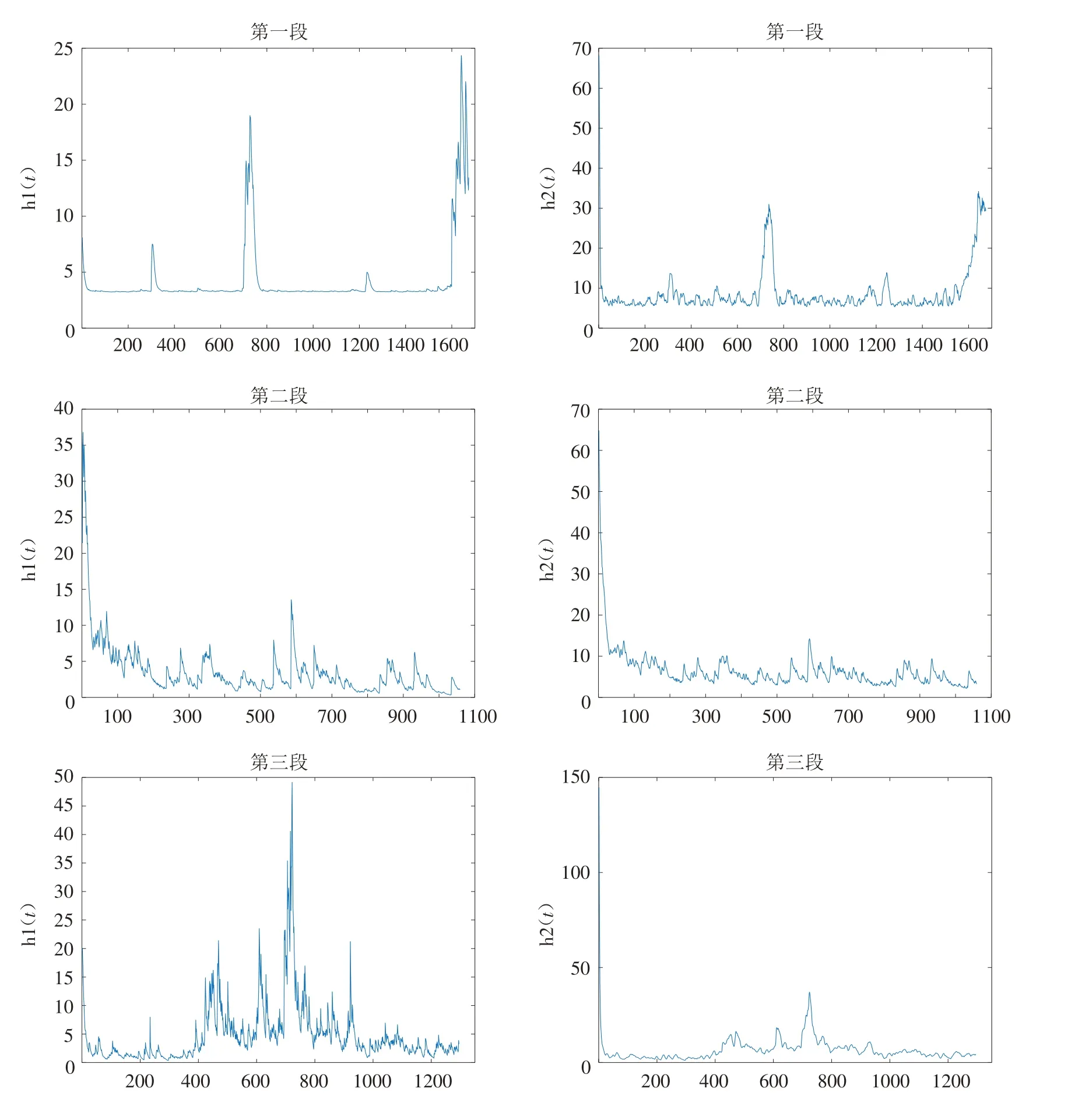
图3 三段时期两种状态的波动率Fig.3 Volatility of two states during the three periods

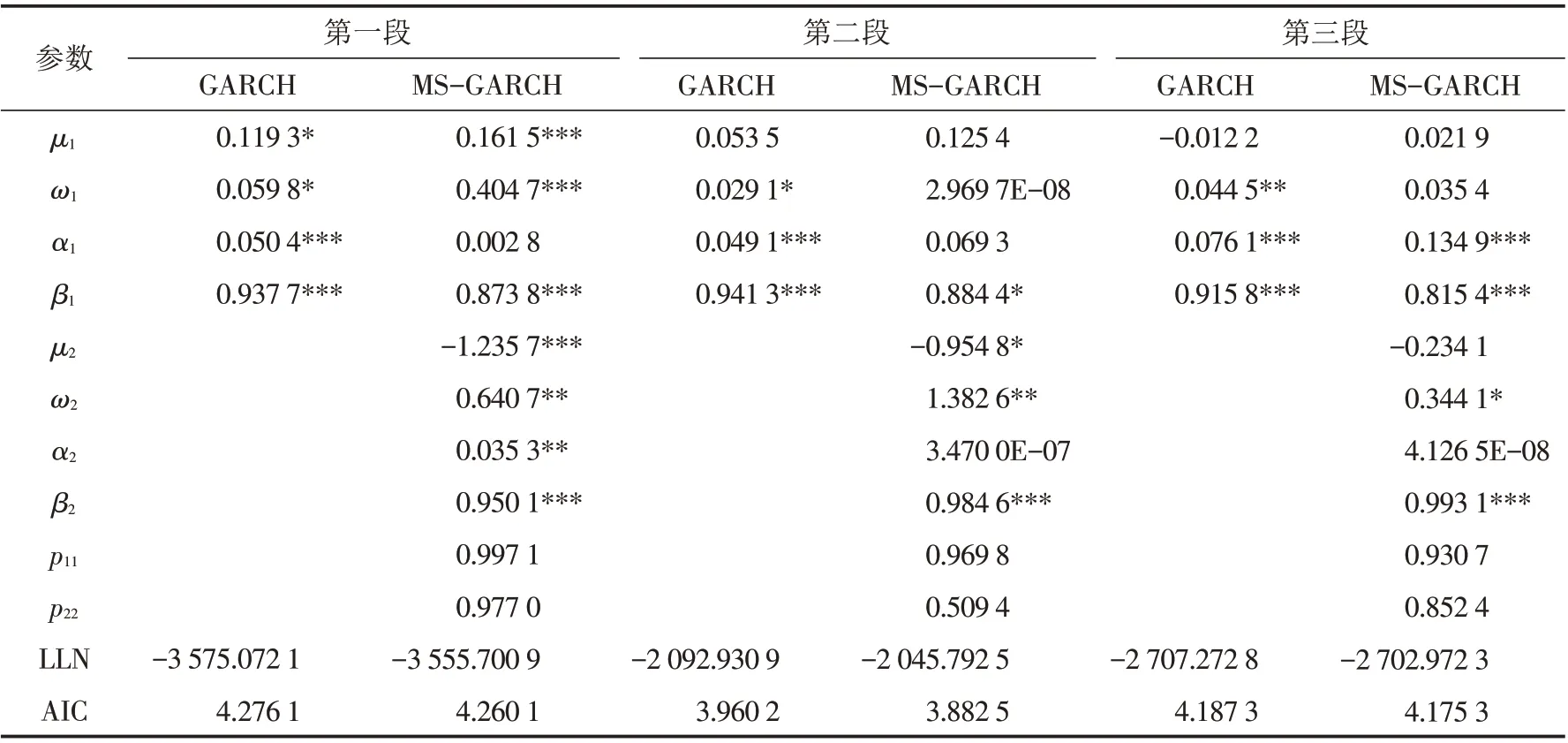
表3 参数估计结果Tab.3 The estimation results of parameters

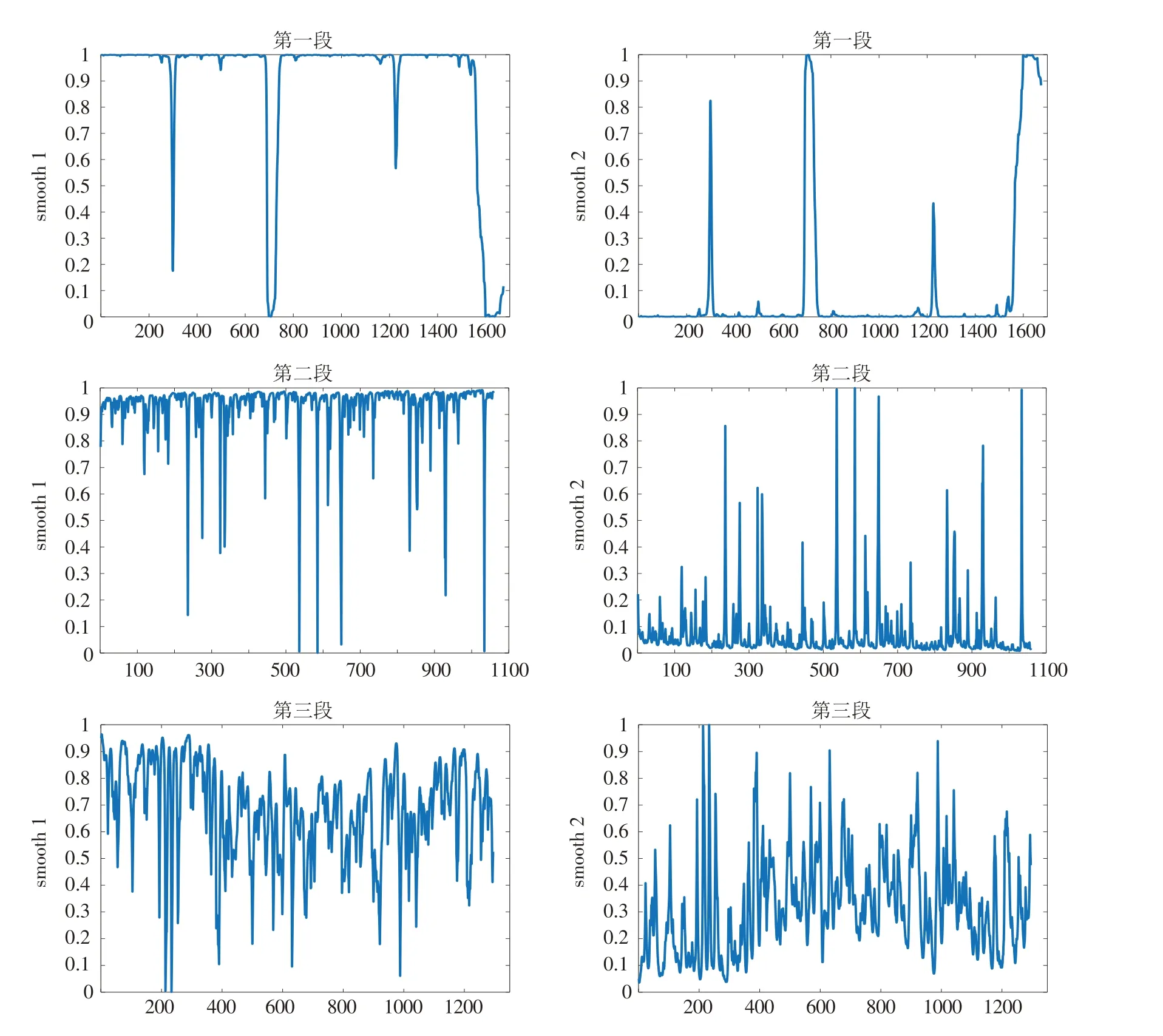
图4 三段时期两种状态的平滑概率Fig.4 Smoothed probabilities of two states during the three periods

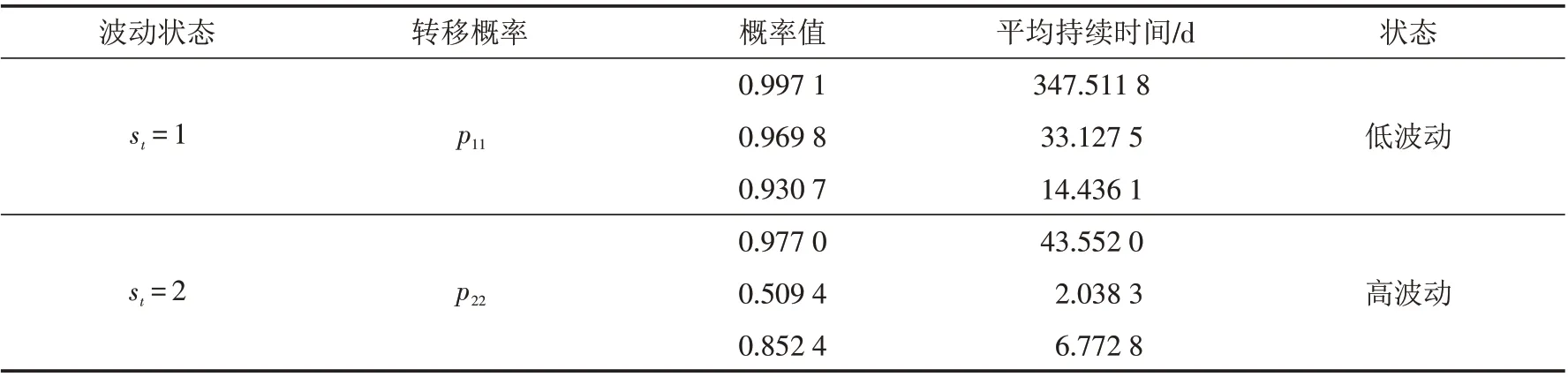
表4 两种波动状态的平均持续时间Tab.4 Average duration of two states

3）对于高波动状态的转移概率p22，在2002-01-02—2008-12-31第一段时期中，概率值为0.977 0，保持高波动状态的可能性较大，说明2001 年底进行的改革对石油价格影响较大，引起大庆石油价格波动. 在2009-01-02—2013-03-28第二段时期中保持高波动状态的概率为0.509 4，而从高波动状态转移到低波动状态的概率为0.490 6，两个概率值相近，表示在此期间内石油价格波动状态易发生转移. 在2013-04-01—2018-05-31这段时间内转移概率值为0.852 4，表示比第二时期要相对稳定地处于高波动状态.

4）整体来看，p11的值要大于p22，说明低波动状态要稳定于高波动状态，高波动状态呈现持续时间较短、不太稳定、易发生转移的特点.

2.3 预测能力评价

对于预测的评价标准，最常见的有公式（12）～（14）所示的三个损失函数：

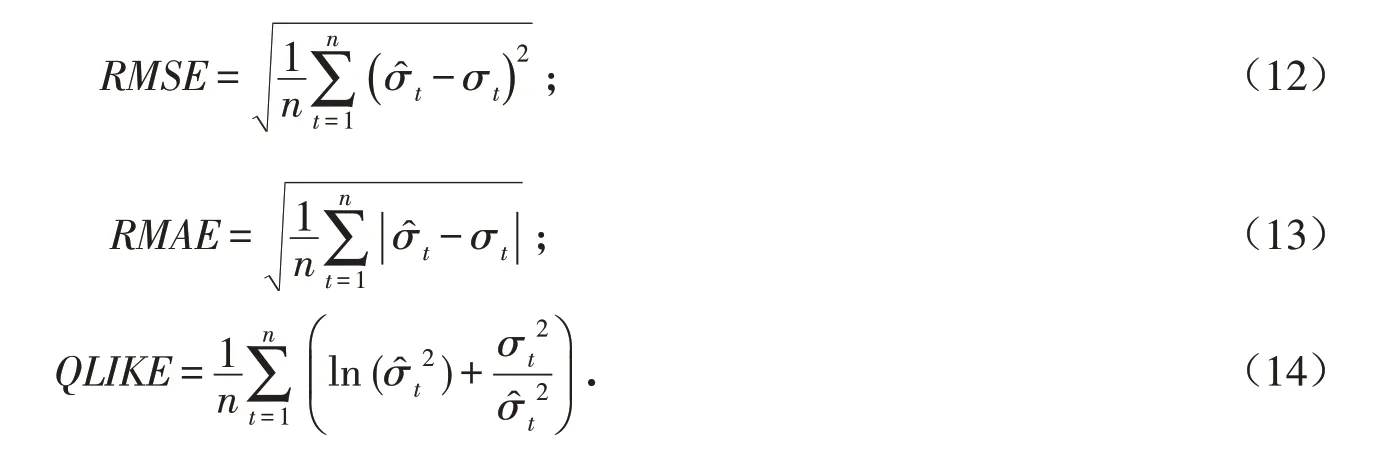
利用GARCH模型的损失函数值与MS-GARCH模型的损失函数值的比值，能更加直观地判断两种模型的预测能力. 当比值大于1时，表示GARCH模型要比MS-GARCH模型的预测能力差；当比值小于1时，表示GARCH模型的预测能力比MS-GARCH模型更好一些. 实证结果见图5和表5.

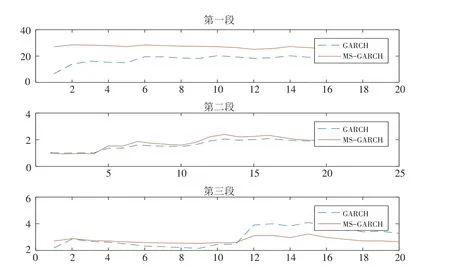
图5 GARCH预测值和MS-GARCH预测值Fig.5 Forecasting results of GARCH and MS-GARCH model

表5 三段时期损失函数值及比值Tab.5 The loss function values and ratio during the three periods

由于在2008 年受到金融危机影响，第一段时期中两个模型的各项损失函数值都较大. 第一段中两个模型的RMSE 比值和RMAE 比值小于1，在第二段时期中只有RMAE 比值小于1，在第三段时期中三项指标比值都大于1，说明最初阶段GARCH 模型的预测精度要高一些，但随着时间发展，MS-GARCH 模型的预测能力要比GARCH 模型更好. 同时也可得出结论：MS-GARCH 模型的出现提高了原油市场波动的预测精度.

3 结论与启示

本文对2002—2018年原油价格进行分段分析，利用GARCH模型和MS-GARCH模型来估计和预测价格波动率. 经过实证研究，得出以下结论：

1）MS-GARCH模型可以帮助我们识别原油波动率的状态转换. 原油市场存在两种波动状态，即高波动状态和低波动状态，但大部分时间市场处于低波动状态，说明低波动状态比较稳定、不会轻易改变，而高波动状态更加容易发生转移. 影响石油价格波动的因素有许多，例如本文提到的石油定价机制改革、2008年金融危机及2016年国际油价暴跌等.

2）根据预测能力评价部分的结果，随着石油价格机制改革的不断深入，开始出现石油价格波动率的两状态趋势. 在2001年底改革后的第一段时期虽然高波动状态明显，但是整体来看依然是GARCH模型的预测能力更好，石油价格的市场开放程度有所局限. 而在后两段时期中，MS-GARCH模型的预测精度明显提高，优于GARCH模型的预测，表示市场正在逐渐成为石油定价的重要机制.

本文研究表明在石油定价机制与国际接轨以来的近二十年中，由于市场化因素的影响，MS-GARCH模型的预测能力要逐渐高于GARCH模型的预测能力，但是这种优越性并不显著，意味着我国石油定价机制的市场化进程还有待进一步推进.

石油产业定价机制关系到我国经济长久持续的发展，继续增强石油产业定价市场化程度，不断完善国内的石油市场，全方位推进市场化改革，有利于增强市场和企业活力，有利于能源经济欣欣向荣、快速发展，有利于提高我国对国际石油定价中的影响力，以及在全球化市场环境下的国际地位［21］. 同时，在市场化发展过程中，政府宏观调控的作用不容忽视，要加强监管能力，要完善石油行业法律法规政策，确保市场在稳定的秩序下公平有效地进行，以促进石油价格机制与国际接轨.