基于FLAC3D隧道开挖的关键命令流

包 昊， 周旭辉， 葛 彬， 方 超

（1.河海大学土木与交通学院，南京 210024； 2.安徽省综合交通研究股份有限公司，合肥 230000）

随着城市化进程的不断加快，地表空间已经不能够满足人们的需求，地下空间的探索已然成为主流. 盾构隧道施工技术是人们对于地下空间探索的最主要的方法之一. 随着工程项目的增多，各地地形的复杂不一，因此隧道的开挖也遇到各种各样的问题，如何较为准确的预测隧道开挖过程中风险，成为国内外学者们尤为关注的问题.

数值模拟分析成为如今分析隧道工程相关问题的重要方式之一. 随着科技的发展，众多商业软件被开发出来用于模拟实际工程问题，与其他软件相较而言，FLAC3D 软件在用于隧道工程的模拟时具有多方面的优势［1］. 首先，隧道开挖时，不同场地的物理力学参数不同，导致不同场地的本构模型之间具有差异，FLAC3D 软件内嵌多种本构模型，可以针对不同的场地进行合理的选择；第二，与实体（group）单元不同的是，该软件本身拥有较多的结构单元用于模拟现实中的衬砌、锚索、梁等，在方便使用者的同时提高了模拟的准确性；第三，该软件为满足更多使用者的要求，其内置的FISH 语言使得参数的赋值以及数据的提取更加人性化. 众所周知，隧道开挖的问题已经得到了广泛的分析［2-8］，而FISH 语言则是建模中必不可少的部分.

本文简要介绍了隧道开挖模拟中关键部分的程序命令流，建立有限差分隧道模型，进行一次隧道开挖对地表位移影响的模拟运算，将结果与Peck［9］经验公式拟合对比，证明其有效性.

1 关键命令

1.1 生成初始地应力场

在采矿工程或者岩土工程领域中，必然存在着初始地应力场，它对于土体变形分析的影响不容小觑. 传统初始地应力场的生成采用弹性求解法，而后再改换成塑性求解，忽略了土体的实际性质. 而采用弹塑性求解法与前述方法相比可产生屈服的区域，相较而言，该方法初始地应力场的生成比前者更为合理.

用简单例子更简易地表达弹塑性求解法的过程：

需要要注意的是此简单例子只为说明生成初始地应力场的过程和方法，将其更为简明地展示出来，由于模型较为简单，故在自重作用之下并没有产生屈服区域，实际情形需要由使用者自己建立适用的模型进行观察分析.

1.2 应力释放

应力释放法实际上就是应力的反向施加. 张传庆等［10］分析了应力释放在隧道工程中的相关问题；程红战等［11-12］在将应力释放系数设为0.1的基础上建立隧道模型，分析了土体弹性模量的相关距离和变异系数对地表变形的影响；方超等［13］将围岩密度、弹性模量、内摩擦角视为三维正态随机场，研究围岩的相关距离对可靠度的影响，其中应力释放系数为0.30. 应力释放方法的原理［14］是当土体开挖以后，在开挖边缘的单元节点上会失去原有的支持力，进行第一步计算（step 1）. 此计算是为了获取其不平衡力P0，将这些不平衡力以某一比例（应力释放系数a）反向施加在原有的节点之上，紧接着添加shell单元进行最后求解. 应力释放后不能进行一次求解计算，必须添加衬砌后两者同时求解，否则隧道先变形后添加衬砌，其隧道掌子面变形量与衬砌变形量不相等，从而脱离实际. 应力释系数的确定与当地的水文地质、开挖施工方法等都有一定关系，需综合分析确定.

具体命令流为：

1.3 设置锚索

在隧道开挖工程的数值模拟中用锚杆和锚索的支护，常常用锚杆对岩石岩土工程进行加固，它的作用是利用水泥沿着长度方向提供的抗剪切能力，以生成局部阻力，借此抵御裂缝的位移变形，但是在目前已有的论文中极少有关于该命令流的介绍. 由于隧道纵向长度远大于横向长度，将其视为平面应变情况，所以建模纵向距离取值1 m，在该范围内的锚杆数量有限，用精确坐标的方法［16］即可完成锚杆布置的数值模拟. 由于锚杆在圆形隧道四周呈放射状布置，故FLAC中的单元都以矩形方块为主，而放射状布置相对于单元形状是难以确定坐标的，可以使用CAD绘制准确图形，从CAD绘图软件中精确读取每根锚杆的坐标位置，并以其中一根锚杆的命令流为例，使用精确坐标法布置隧道四周的锚杆命令流：

用该方法建立锚杆需输入每个点的坐标，故不适合较多坐标点的输入，否则既繁琐又容易出错，需慎重选择. 锚杆一般与衬砌连用，共同作用于隧道掌子面，使得隧道变形降为最小值，就如上面添加衬砌一样，锚杆的添加也不是一步完成的，需要在此之前进行应力释放，由于前面已经定义了FISH语言，这里不再复述.利用应力释放程序、衬砌（shell）单元、锚杆（cable）等建立较为完善的隧道开挖模拟.

2 隧道有限差分建模

以在上海地区的软黏土中开挖隧道为原型，模拟在均质土体中开挖隧道对邻近建筑物的影响. 有限差分模型的几何形状如图1所示，土体的宽度为120 m，深度为50 m，较大的边界有利于减少计算变形的误差.隧道的衬砌用shell单元来模拟，由于在FLAC3D中shell单元为弹性连续环，这与实际衬砌的组装不相符，故需要对衬砌刚度进行折减，折减系数取0.7. 隧道的轴线埋深为15 m，如表1所示，隧道的外径为6.2 m，内径为5.5 m，衬砌厚度为0.35 m. 由于隧道的纵向尺寸远远大于其截面的尺寸，故同前所述，纵向取值1 m假设为平面应变情形. 假设衬砌为混凝土材料，其弹性模量、泊松比和重度分别为34.5 GPa、0.2和25 kN/m3.

表1 物理力学参数Tab.1 Physico-mechanical parameters

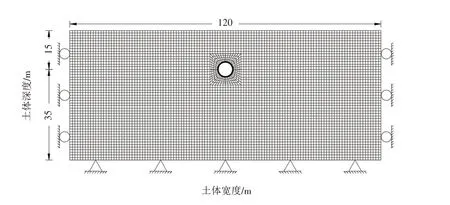
图1 有限差分模型Fig.1 Finite difference model

在各种数值模拟中，已有大量的土体模型用于模拟软土的非线性应力应变的特性. 然而获得准确的土体参数进行合理的预测较为困难，故本研究采用Mohr-Coulomb 模型，这也是目前在模拟土体模型中应用最为广泛的数值模型之一.表1给出了土体参数，这是上海软黏土的常用值［17］. 采用应力释放法开挖隧道，典型的上海软黏土的应力释放率为25%～30%，结合有限差分模型以及上海隧道的实际情形，本文的应力释放率取值0.25. 均质土的地表位移如图2 所示，该曲线能用Peck的经验公式较好地拟合，基本服从高斯分布，也说明该有限差分模型可以有效地模拟隧道开挖引起的地表变形规律.

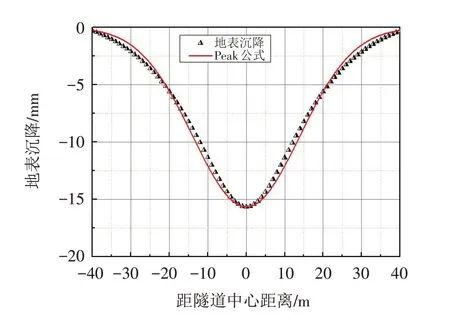
图2 地表沉降与曲线拟合Fig.2 Surface settlement and curve fitting

3 结语

1）FLAC3D在分析隧道工程和采矿工程问题时具有较大的优势，内含的结构单元和本构模型可更为简便与准确地进行数值建模. 但在模型较大、单元数量较多时，其计算过程较长，计算速度会显得较慢.

2）传统的初始地应力场的生成虽然简便，但与实际有一定差距. 通过改变强度参数的弹塑性法建立初始地应力场可优化这一过程，可反映土体的塑性区，但其计算速度亦会随着模型的增大减慢.

3）使用应力释放法进行隧道开挖，可以在一定计算条件下较好地还原实地情形，但是由于应力释放率的确定与各种因素有关，故需综合确定.

4）用FLAC3D 建立有限差分模型，所得隧道开挖对地表位移的沉降曲线符合Peck 经验公式，具有一定的有效性.