基于静态贯入试验法研究无黏性土管涌发生后抗剪强度变化规律

陈 亮， 余 旺， 罗春木， 何健健

（1.河海大学岩土力学与堤坝工程教育部重点试验室，南京 210098；2.河海大学土木与交通学院，南京 210098； 3.国网常州市金坛区供电分公司，江苏常州 213200）

管涌是指土体在渗流作用下细颗粒通过粗颗粒之间的孔隙而移动的渗透变形现象. 当坝基受到渗流冲刷时，容易发生管涌侵蚀，管涌侵蚀增大土体的孔隙通道和渗透性，降低坝基强度，造成堤坝的发生，是大坝安全运行的隐患［1-2］.

由于管涌发生过程中不断发生细颗粒流失，导致管涌后无黏性土的颗粒级配发生较大变化，甚至产生较大沉降，进而影响无黏性土的力学特性［3-4］. 目前，已有学者研究无黏性土管涌发生后的力学性质变化.其中，罗玉龙［5］认为孔隙水渗流冲刷土骨架产生可动细颗粒，可动细颗粒跟随孔隙水渗流运移流失，土颗粒重新排列、沉积，导致无黏性土细观结构和力学特性发生改变；Sterpi［6］利用常规三轴试验仪器进行管涌侵蚀试验，发现细颗粒的流失会逐渐改变无黏性土的抗剪强度，影响无黏性土弹性模量、内摩擦角和泊松比；Ke 和Takahashi［7-8］通过室内一维渗流方向自下而上的管涌试验，发现细颗粒流失会导致无黏性土孔隙率、渗透性的增加，土体抗剪强度降低；Chang［9］等对管涌侵蚀后的无黏性土进行三轴压缩试验，发现在大量细颗粒损失后，土壤的峰值剪切强度降低，但是临界状态下的剪切强度随着细颗粒的损失而略微增加；杨咏梅［10］利用自研管涌侵蚀—渗流—应力耦合试验系统，研究管涌过程中细颗粒流失量对无黏性土抗剪强度的影响，发现颗粒级配对于散粒土管涌发生后无黏性土抗剪强度具有较大影响，无黏性土细颗粒越多，可以流失的细颗粒也越多，无黏性土抗剪强度变化越大；Chen［11］通过三轴压缩试验，在内部侵蚀过程中采用了一种侵蚀控制的实验方法来达到指定细颗粒的流失量，研究由于管涌而导致细颗粒流失后的土体应力-应变状态，发现在大量细小颗粒流失后，土体的应力-应变状态从最初的剪涨行为转变为一种压缩的行为.

前人研究管涌发生后无黏性土抗剪强度的方法多基于三轴压缩试验，而三轴试验的仪器研制成本较高、操作较为繁琐，与之相比，静态贯入试验有着仪器研制成本低、操作简单的优势. 因此，本文通过自制贯入系统，对不同细颗粒含量试样进行管涌发生后的静态贯入试验，分析总结了无黏性土细颗粒含量、管涌过程中的水力梯度及细颗粒流失量等因素对无黏性土发生管涌发生后抗剪强度变化的影响.

1 试验概况

1.1 试验仪器

本文自制圆柱体管涌发生试验槽，如图1 所示.试验槽的材料采用有机玻璃，以便于观察试样细颗粒运移情况，其高为50 cm，内径为140 mm. 在试验槽的侧壁从上到下每隔5 cm设置一个水压力传感器接口，共8个水压力传感器，编号从下到上依次为1～8，1号水压传感器距离试验槽底部100 mm. 水流从下而上流过试样. 为使水流均匀流入，在离试验槽底部100 mm处设置隔水透板，并在高度的1/3 和2/3 处应分别设置边界控制环，配合装样时在侧壁涂抹的凡士林一起防止试样与模型接触面上的优先发生.

1.2 试验材料

试验材料由粗颗粒和细颗粒按4∶1的比例配比组成. 粗颗粒为粒径2.0～8.0 mm 的细砾，在试样中充当骨架作用；细颗粒为粒径0.075～0.25 mm 的细砂，充填在粗颗粒骨架形成的孔隙中. 本次试验的各组试样细颗粒含量最大为25%，均为管涌型土［12］. 按细颗粒含量的不同，把试样分为4 组，编号分别为FC10，FC15，FC18，FC25，代表不同的细颗粒含量. 试样级配曲线如图2，配比参数见表1.

1.3 试验过程

1）烘干试样. 将试样放进烘箱烘干，温度设为105 ℃，持续24 h，保证试样干燥.

图1 管涌发生装置示意图Fig.1 Schematic diagram of piping device

图2 试样级配曲线Fig.2 Sample grading curve

表1 试验材料物理性质Tab.1 Physical properties of test materials

2）制样装样. 按粗细颗粒4∶1配制试样；试样分4 层分别装入圆筒，每2～3 cm压实，每层装样后用木槌轻轻击实到一定厚度，为了保证每层土样的孔隙比基本一样，在厚度一定的情况下，使每层装样土料的质量一样，通过控制干密度间接保证每层土样的孔隙比一致.

3）饱和试样. 通过提高试验槽装置底部连接的水箱进行供水，缓慢提升水箱，当水箱水位略高过试验槽顶部时固定，饱和24 h.

4）开始试验. 从饱和水头开始，通过提高水箱的方式，每3～4 cm缓慢提高一次水头，每级水头固定30 min，记录每级水头下试样稳定时的孔压及流量，当试样表面出现大面积细颗粒堆积时，停止提高水头，让试样在稳定的发生水头下不断冲刷，当细颗粒不再流失后，将水箱降至试样饱和的高度，试样稳定后行进行静态贯入试验.

2 管涌试验分析

目前已有许多关于管涌临界水力梯度的理论公式［13-15］，本文确定临界水力梯度的方法是取细颗粒被轻微冲刷出时所对应的水力梯度以及水力梯度与流速关系曲线的拐点时所对应的水力梯度两者中的较小值［16］，作为管涌临界水力梯度.

图3 为试样管涌发生过程. 试样饱和时（图3a），试样中的细颗粒保持稳定状态，没有发生颗粒移动现象；随着上游水头不断增加，部分细颗粒开始移动，从装置侧壁可以发现有轻微的细颗粒跳动现象，试样顶面变浑浊；当上游水头到一定高度时（图3b），试样侧面细颗粒跳动剧烈，顶面出现细颗粒跳动的现象，部分细颗粒运动至试样顶面，并轻微堆积，此时的水力梯度为0.75；保持上游水头不变（图3c），随着时间的增加，试样顶面细颗粒大面积覆盖，出现明显的管涌口，形成集中渗流通道.

图3 试样管涌发生过程Fig.3 Piping process of samples

图4为流速随水力梯度的变化关系曲线. 在试验刚开始时，水力梯度与流速近似线性关系，说明土体渗流稳定，符合达西定律. 当曲线斜率开始发生变化时，试样顶面出现细颗粒跳动并轻微覆盖的现象，对应的水力梯度为0.22，小于试样细颗粒流出时所对应的水力梯度. 至此，试样开始发生管涌发生，将此时的水力梯度定义为临界水力梯度. 以此方法确定各组试样的临界水力梯度，见表2.

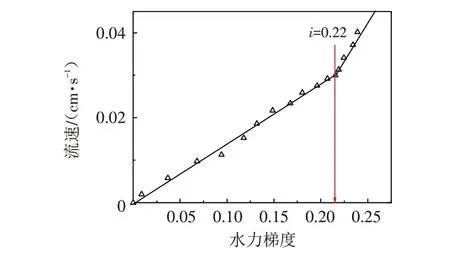
图4 流速与水力梯度关系Fig.4 Relationship between velocity of flow and hydraulic gradient

表2表明无黏性土的临界水力梯度随着细颗粒含量的增大而增大. 这是因为，当细颗粒含量不高时，无黏性土的渗透变形能力取决于细颗粒填充粗粒孔隙的程度. 细颗粒含量越少，粗粒孔隙填充程度越低，越容易发生渗透发生，反之当细颗粒含量越高时，就越难发生渗透发生.

表2 各组试样临界水力梯度Tab.2 Critical hydraulic gradient of each sample

3 贯入试验分析

贯入试验所采用的仪器包括普式贯入仪和加载系统两部分. 贯入仪采用普式贯入仪（图5），可测定不同深度处土的贯入阻力. 普式贯入仪包括主机、探杆和探头三部分. 测量范围为0～100 kg（即0～1000 N）；测试深度为0～30 cm；精度≤0.5%.加载系统由手摇式千斤顶和反力装置组成.

室内静态贯入试验需要考虑尺寸效应的问题，即试样颗粒粒径、贯入仪探头尺寸及圆柱体试验槽尺寸应满足一定条件，否则会影响试验测试结果. Ke和Takahashi等进行过相关方面的研究，发现松散状态下的无黏性土受尺寸效应影响很小，中密和密实状态下的无黏性土受尺寸效应影响较大. 本文贯入试验的探头直径为10 mm，试验槽直径为140 mm，比值n=14，如图6 中虚线所示，各组试样Dr=0.3，因此本次试验不需要考虑尺寸效应的问题.

图5 贯入仪器Fig.5 Penetration instrument

图6 承载力系数与试验槽直径和探头直径比值的关系Fig.6 Relationship between bearing capacity coefficient and ratio of test tank diameter and probe diameter

为避免试样发生扰动，使试样发生后一直处于饱和状态，利用贯入仪直接在原样上进行贯入试验. 由于该贯入试验具有较好的可重复性，且管涌发生后试样顶面管涌口位置及试样内部管涌通道位置并非均匀分布. 因此，每组试验均选取5 个贯入点，其位置分布如图7所示. 贯入过程中应连续、平稳地摇千斤顶扳手，保证贯入速度均匀，不可太快，每隔1 cm记录一次读数.

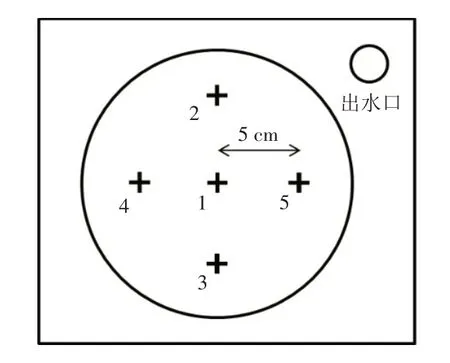
图7 贯入点位置Fig.7 Penetration point position

3.1 理论依据

已有研究理论将贯入试验测得的贯入阻力与无黏性土的力学特性通过内摩擦角进行联系，使贯入试验测试结果能够运用到工程上. 已有研究发现贯入阻力对砂土的剪切强度的影响大于压缩系数［17］，因此，贯入试验数据可为承载力理论提供合理的计算依据. 根据已有研究，本文将承载力系数Nq和内摩擦角φ与贯入试验测得的贯入阻力P相关联，计算方法如下：

式中：A1、A2为回归系数；ΔP为贯入阻力增量；Δ σ′v为竖向有效应力增量. 其中，竖向有效应力增量可按下式计算：

式中：ρ′为土体浮密度，g/cm3；Δh为竖向高度增量，cm；Gs为土粒比重；n为孔隙率；ρw为水的密度，取1 g/cm3.

由于贯入试验涉及的最大试样渗径长度为25 cm，按式（4）计算得试样最大浮密度为1.27 g/cm3，计算得试样顶面至底部的有效应力增量为0.311 N/cm2，而贯入阻力在深度为15 cm以上时，均大于200 N. 由此可知，承载力系数Nq与贯入阻力增量ΔP呈正比关系. 根据已有研究资料［18］，回归系数A1、A2均大于零. 由此可知，土体内摩擦角φ与贯入阻力增量ΔP呈正比关系，而砂土的抗剪强度表达式，如式（5）所示，直接与内摩擦角相关. 因此，可通过贯入阻力的变化情况间接反映砂土的抗剪强度变化情况.

式中：τf为土的抗剪强度，kPa；σ为滑动面上的法向应力，kPa；φ为土的内摩擦角.

3.2 力学性质变化规律

3.2.1 细颗粒含量的影响 为了研究试样细颗粒含量对无黏性土力学性质的影响［19-20］，分别绘制试样未发生管涌和管涌发生后两种工况下，不同细颗粒含量试样的贯入阻力随贯入深度的变化情况，如图8所示.

图8（a）为四种不同细颗粒含量试样，在管涌发生前的贯入阻力随贯入深度的变化情况. 由图可知，试样FC10、FC15 和FC18 的力学特性较为接近，而试样FC25 在相同贯入深度处的贯入阻力明显大于另外三组. 这是因为四组试样的相对密实度均为0.3，土体处于松散状态，细颗粒在土体中主要起填充粗颗粒形成的孔隙的作用，试样FC25的细颗粒含量明显高于另外三组试样，其对应的孔隙比最小，因此力学特性最好.

图8（b）为四种不同细颗粒含量试样，在管涌发生后的贯入阻力随贯入深度的变化情况. 从图8（b）中可以看出，管涌发生后试样FC25在同等贯入深度处的贯入阻力变为最小，而另外三组试样较为接近；且与图8（a）对比可知，管涌发生后，试样FC10、FC15和FC18的力学特性变好，而试样FC25的力学特性变差.

试样FC10、FC15、FC18、FC25均为松散状态（Dr=0.3），当无黏性土细颗粒含量较大（FC≥25%）时，细颗粒在土体中除了起填充孔隙作用外，还起传力介质作用，管涌发生后，由于起传力介质作用的细颗粒的流失，导致土体变得更加松散，且孔隙比变大，因此土体在管涌后力学特性下降了. 若无黏性土细颗粒含量较少（FC≤18%）时，细颗粒只起填充孔隙作用，不充当传力介质，所以管涌发生后，虽然细颗粒流失导致土体孔隙比变大，但其传力结构变化较小，且由于填充在粗颗粒孔隙间的细颗粒的流失，使得粗颗粒间发生相对移动时少了细颗粒的润滑作用，因此土体在管涌后力学特性得到提升.

3.2.2 细颗粒流失量的影响 由于管涌发生过程中不断发生细颗粒流失［21-23］，土体管涌发生后的总细颗粒流失量间接反映了土体内部结构的变化情况，对土体的力学特性有较大影响. 为了研究管涌后细颗粒流失量对无黏性土力学特性的影响，取每组试样的五组贯入数据的平均值作为该组试样的贯入数据，分别绘制各组试样在管涌发生过程中，发生不同细颗粒流失时的贯入阻力随贯入深度的变化情况，如图9所示.

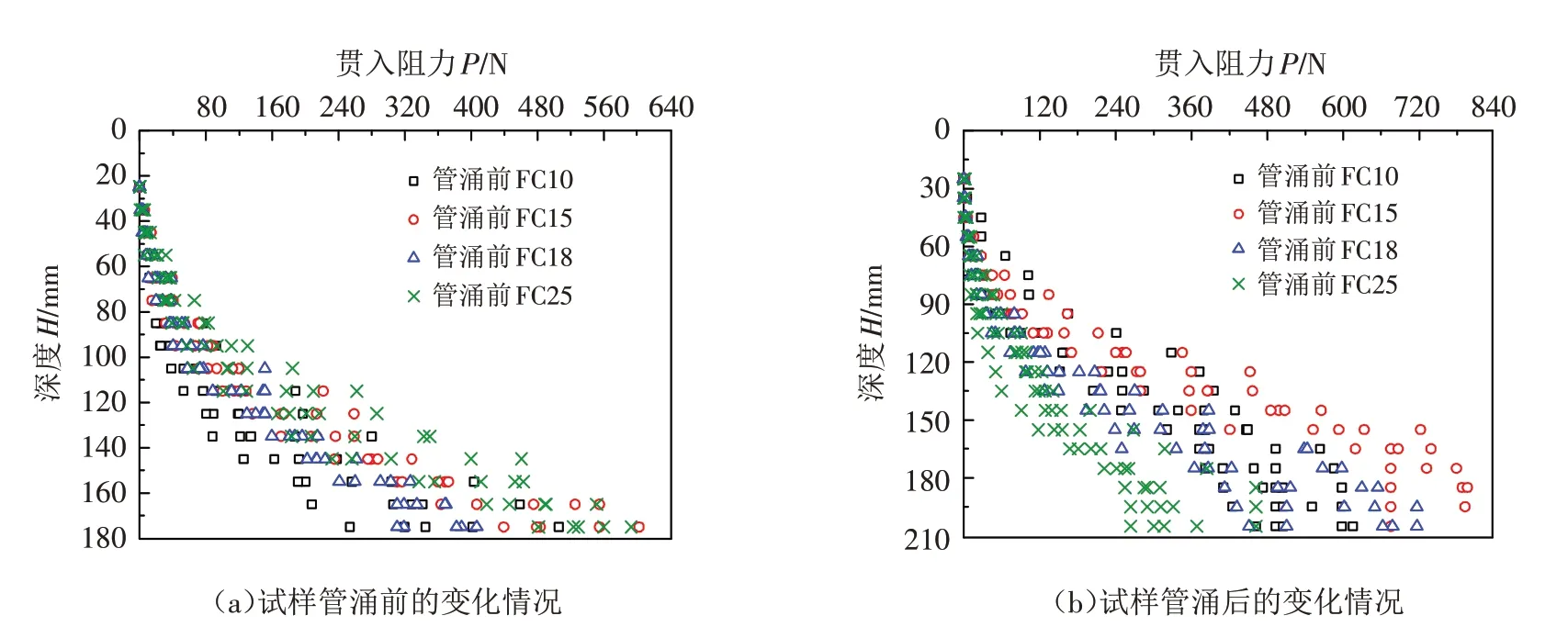
图8 细颗粒含量对无黏性土力学特性的影响Fig.8 Effect of fine particle content on mechanical properties of non-cohesive soil

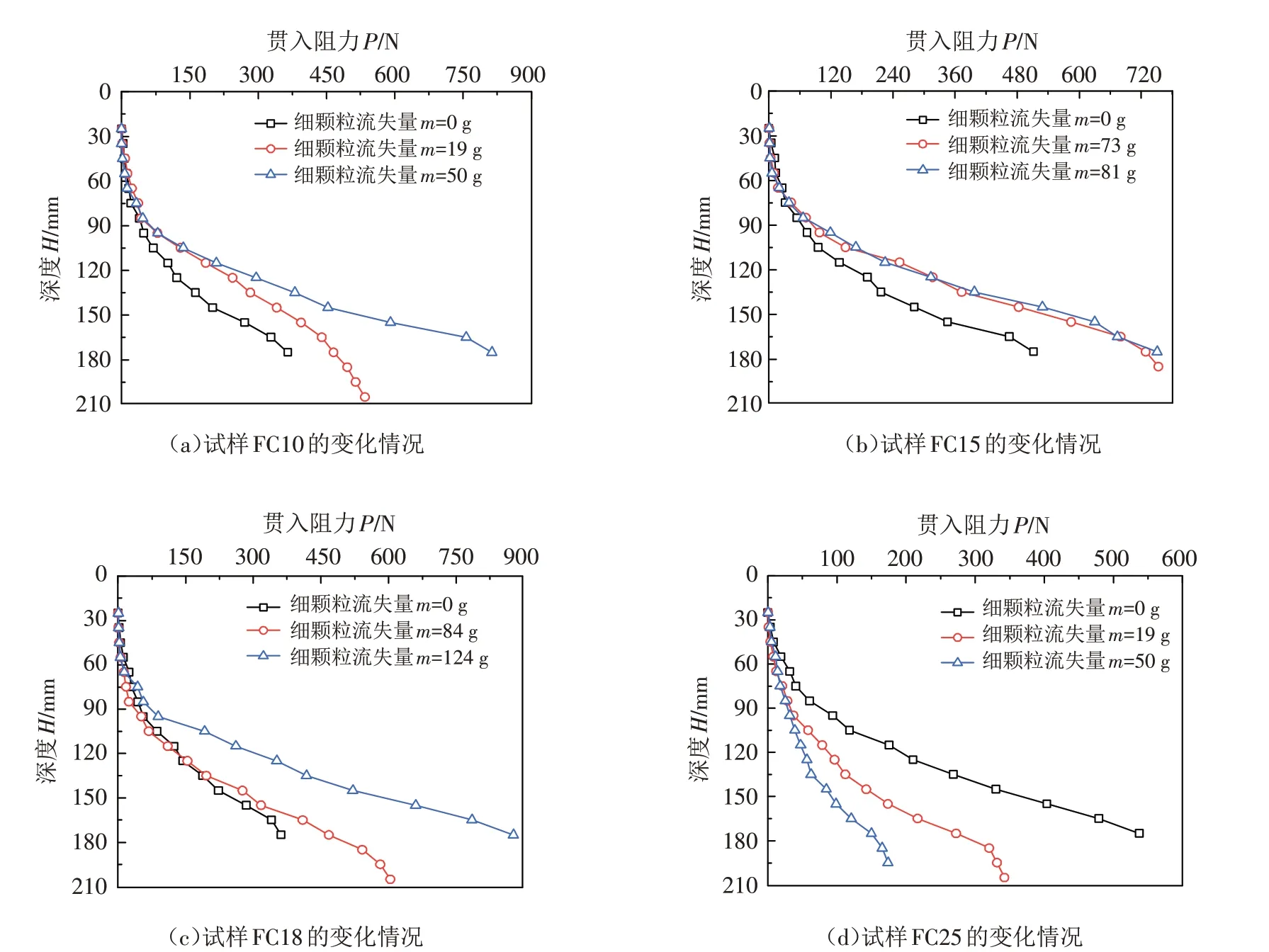
图9 细颗粒流失量对无黏性土力学特性的影响Fig.9 Influence of the loss of fine particles on the mechanical properties of non-cohesive soil

由图9 知，管涌发生后试样的贯入曲线发生偏移，且偏移量和试样的细颗粒流失量有关. 其中，试样FC10、FC15、FC18随着试样细颗粒流失量的增大，相同贯入深度处的贯入阻力也随之增大；试样FC25随着试样细颗粒流失量的增大，相同贯入深度处的贯入阻力逐渐减小. 即无黏性土细颗粒含量较小时，其贯入阻力随管涌过程中细颗粒流失量的增大而增大；当无黏性土细颗粒含量较大时，其贯入阻力随管涌过程中细颗粒流失量的增大而减小. 其原因和3.2.1的分析一致.

3.2.3 水力梯度的影响 当作用在土体上的水力梯度不同时，土体在管涌发展过程中各参数变化规律也将不同［24］，从而导致管涌发生后土体的力学性质的不同. 为了研究作用在试样上的水力梯度对该水力梯度下发生管涌发生后无黏性土的力学特性的影响，绘制各组试样在不同水力梯度下发生管涌发生后的贯入阻力随贯入深度的变化情况，如图10所示.

图10 管涌水力梯度对无黏性土力学特性的影响（i0为作用在试样上的最大水力梯度）Fig.10 Influence of piping hydraulic gradient on mechanical properties of non-cohesive soil（i0 is the maximum hydraulic gradient acting on the specimens）

由图10知，管涌发生后试样的贯入曲线发生偏移，且偏移量和管涌时作用在试样上的最大水力梯度有关. 其中，试样FC10、FC15、FC18随管涌时作用在试样上的最大水力梯度的增大，相同贯入深度处的贯入阻力随之增大；试样FC25随管涌时作用在试样上的最大水力梯度的增大，相同贯入深度处的贯入阻力随之减小. 即无黏性土细颗粒含量较小时，其贯入阻力随管涌时作用在试样上的最大水力梯度的增大而增大；当无黏性土细颗粒含量较大时，其贯入阻力随管涌时作用在试样上的最大水力梯度的增大而减小.

4 结论与展望

本文通过对不同细颗粒含量试样进行静态贯入试验，结合试验数据对管涌发生后无黏性土抗剪强度的变化规律进行研究，得到以下结论：

1）无黏性土处于较松散状态时，不同细颗粒含量试样在管涌前的抗剪强度较为接近；管涌发生后，细颗粒含量较低的试样的抗剪强度得到提高，而细颗粒含量较高的试样的抗剪强度有所降低.

2）管涌后无黏性土的抗剪强度与管涌过程中的细颗粒流失量呈以下变化关系：当无黏性土细颗粒含量较小时，其抗剪强度随管涌过程中细颗粒流失量的增大而增大；当无黏性土细颗粒含量较大时，其抗剪强度随管涌过程中细颗粒流失量的增大而减小.

3）管涌后无黏性土的抗剪强度与管涌时作用在土体上的最大水力梯度呈以下变化关系：当无黏性土细颗粒含量较小时，其抗剪强度随管涌时作用在试样上的最大水力梯度的增大而增大；当无黏性土细颗粒含量较大时，其抗剪强度随管涌时作用在试样上的最大水力梯度的增大而减小.

4）由于静态贯入试验存在尺寸效应的问题，因此本文只针对较为松散的无黏性土展开研究，而对于中密和高密的无黏性土是否适用有待进一步讨论.