基于遥感和GIS的烟台芝罘湾海岸线变迁研究

孙贵芹徐艳东*林 蕾朱金龙赵景丽魏 潇

(1.山东省海洋资源与环境研究院 山东省海洋生态修复重点实验室,山东 烟台264006；2.中国科学院 遥感与数字地球研究所,北京100101)

海岸线是多年平均大潮高潮时形成的实际痕迹线[1],具有复杂、敏感和多变的特征,它的变化直接影响着潮间带滩涂资源量、海岸带的环境以及沿海地区人民的生存和发展[2]。国内外对于岸线变化的研究取得了丰硕的成果。在岸线提取方法方面,岸线类型的识别主要靠目视解译,而岸线位置的提取根据是否需要人为修改分为自动、半自动和目视解译三种方法,如:利用高分辨率SPOT遥感影像和精细DEM数据可实现岸线自动提取[3]；基于多源遥感数据,利用改进的水边线方法,结合部分实测潮位、坡度数据可提取多时相海岸线[4]；利用密度分割法、面向对象分类方法提取水边线,并结合目视解译可获取研究区海岸线[5]；基于SPOT影像,结合实地踏勘资料和经验,建立各类型岸线的遥感解译标志,可人工提取较为准确的岸线位置[6]。在岸线的分析研究方面,岸线变化的研究方法经历了简单视觉定性分析、简单统计量分析、简单线性模型拟合分析、复杂非线性模型拟合分析等阶段,而岸线变化的研究内容从特征的简单描述发展为对引起岸线变化的内在机理与机制的探讨[7],如:国外学者综合多源数据,采用地图叠加的方式,对牙买加里约米尼奥河(the Rio Minho River,Jamaica)至米尔河(the Milk River)入海口间岸线的变化进行定性分析[8]；基于航片从海陆面积变化方面对土耳其黑海中部萨姆松市(Samsun,Turkey)的海岸线变化特征进行简单定量分析[9]；综合运用RS和DSAS(数字岸线分析系统)对印度[10]、越南湄公河三角洲[11]等地区的海岸线进行简单模型定量化分析,并利用卫星影像和统计方法对孟加拉湾[12]海岸线进行了时空变化分析和预测；基于复杂模型的IC-bin[13]和T-bin[14]局部模拟方法对夏威夷毛伊岛岸线变化速率及岸线位置进行分析和预测；而国内学者针对岸线变化的研究多集中于对岸线基本特征的分析,例如对我国大陆沿海主要海湾形态变化[15]的研究；对我国大陆海岸线[16-18]、北方海岸线[2]、渤海[19-21]、江苏[22]、浙江[23]、大连[24]、长岛南五岛[25]的海岸线时空变迁[22-23,25]、岸线分形特征的时空变化[17-18,26]及原因[16,20]分析等。

芝罘湾位于山东烟台市区北部,其西侧和北侧为我国最大的陆连岛——芝罘岛。湾口向东敞开,为“U”字形半封闭式海湾,湾顶为砂质海岸,两侧是基岩海岸,湾内水深一般在10 m以内。该湾水域开阔,湾口东侧的崆峒岛群形成天然屏障,使得湾内浪小流稳,由此成为山东半岛北部的天然良港[27]。随着快速城市化进程,芝罘湾受到人类活动的强烈影响,海岸线不断向海推进,大量自然岸线被占用,人工岸线比例逐渐占据主导地位,围填海面积持续增加,海湾面积不断萎缩,生态环境遭到严重破坏,这受到了一些学者的关注,随之,学者们主要开展了一些研究,包括:基于遥感和GIS技术分析了烟台典型海湾1986—2004年4个时期的海岸线长度和海湾面积的变化[28]、烟台市海岸地区1990—2009年土地利用空间格局变化[29]、1973—2014年烟台市岸线及近岸土地利用变化[30]、1979—2007年芝罘区土地利用变化及芝罘连岛沙坝岸线变化[31]以及烟台市1990—2015年5个时期的围填海动态变化及驱动力[32]等。然而,这些研究的对象主要是整个烟台地区,截至目前尚未有系统研究芝罘湾长时段岸线变迁的报道。本文正是以芝罘湾为研究对象,开展1976—2016年近40 a长时间序列岸线时空变迁的研究,掌握9个不同时期的岸线时空分布特征和变化过程及海湾形态变化,以期为芝罘湾岸线的合理利用及海岸带经济的可持续发展提供重要的理论依据。

1 材料与方法

1.1 研究区域

芝罘湾口门北起芝罘岛东南角(121°25'54″E,37°35'48″N),南至东炮台山(121°25'47″E,37°37'07″N)[33]。根据实际研究需要,将芝罘湾口门的起止点调整为 A(121°25'57.11″E,37°35'43.67″N)和 D(121°25'49.73″E,37°32'6.86″N)。为进一步研究不同岸段的分异特征,将研究区岸线划分为3个岸段进行研究,其中芝罘岛东南角(A)至大疃岛码头西侧(B)为北岸,大疃岛码头西侧(B)至一突堤东侧(C)为西岸,一突堤东侧(C)至东炮台山(D)为南岸,研究区位置和岸段划分见图1。

1.2 数据来源

选用芝罘湾1976—2016年每5 a为一个时期(共9期)Landsat遥感影像,作为海岸线提取的数据源,数据来源于美国地质调查局(United States Geological Survey,USGS)网站①http://glovis.usgs.gov和地理空间数据云网站②http://www.gscloud.cn。在保证影像质量的前提下,尽量选择大潮高潮时期的影像数据。为提高解译精度,借助谷歌地图、天地图、2004-11的烟台市SPOT5融合正射校正图像进行辅助解译。本文所采用的遥感影像数据源情况见表1。

1.3 研究方法

1.3.1 影像处理及岸线提取

为保证遥感影像的几何精度,首先在ENVI 5.1中对遥感影像进行预处理,然后以一幅经过正射校正的2016年高分影像为基准,对1996年遥感影像进行几何精校正,以校正好的1996年影像对其他几期遥感影像分别进行配准。采用二次多项式模型,双线性内插法进行重采样,校正配准误差控制在0.5个像元以内。并将9期影像统一为高斯——克吕格投影、CGCS2000坐标系,采用近红外、红、绿波段生成标准假彩色影像,通过线性拉伸对图像进行增强处理,综合孙伟富等[6]、毋亭等[7]、赵建华等[34]的遥感监测分类方法建立各类岸线的解译标志和判绘原则,采用目视解译法获取岸线。为提高岸线解译精度和准确性,先利用2016年的高分遥感影像提取2016年芝罘湾海岸线,在此基础上,向前逐期提取各个时相下的海岸线,着重对变化的岸段进行矢量编辑。

1.3.2 岸线提取误差分析

遥感影像获取的岸线只能代表某一特定时间的海陆分界线,且岸线的提取受人为因素影响较大,导致提取结果与实际岸线存在一定差异。因此,对提取岸线进行误差分析以满足特定研究的需要是十分必要的。在缺乏足够数量的高精度实测控制点的情况下,根据Fletcher等[35]、闫秋双等[36]、毋亭等[7]的研究,最终的岸线数据提取误差可以采用多误差综合法[35],将岸线提取过程中的数据源误差、影像处理误差等一系列潜在的误差项计入最终的误差E计算中,公式为

式中,es为季节误差,etd为潮差误差,ep为像元误差,ed为数字化误差,er为校正误差。本文选取的遥感影像均处于春秋两个季节,且研究区自然岸线以基岩和砂质岸线为主,基本不受植被的影响,因此,季节误差(es)可以忽略不计；研究区大部分为人工岸线和基岩岸线,因此,受潮汐影响(etd)也可忽略不计；本文的岸线提取方法能达到亚像元精度,所以像元误差(ep)也不考虑；为减小数字化误差(ed),本文的岸线解译工作均由一人完成。因此,根据式(1),仅考虑数字化误差(ed)和校正误差(er),计算的岸线提取总误差见表2。

高山[37]、侯西勇等[38]研究表明,60,30和2 m分辨率遥感影像线要素提取的最大允许误差分别为56.57,28.28和1.89 m。本文的岸线提取误差均小于一个像元,明显小于理论最大允许误差,表明岸线提取的方案是可行的。为了进一步验证本文误差分析方法的有效性,利用2005年的“我国近海海洋综合调查与评价专项”(简称“908专项”)修测岸线对提取的2006年岸线进行精度验证,结果表明,提取的2006年岸线到“908专项”修测岸线的标准偏差为13.81 m,与本文所采用的误差分析方法得到的岸线总误差(11.37 m)较为接近。因此,本文的岸线提取方法是可行的,能够满足岸线遥感解译的精度要求。

1.3.3 海湾形状指数

海湾形状指数是指海湾周长与等面积圆周长之比,反映海湾形状与圆形的相似度；值越小,海湾形状越规则、简单；反之,则越复杂。海湾形状指数(SIB)计算式[15]为

式中,P为海湾周长(m)；A为海湾面积(m2)。

1.3.4 海湾重心

在二维平面空间中,计算得到海湾几何重心,其空间位移的方向、路径和距离可以反映出海湾形态变化的基本特征[15]。海湾重心坐标(x,y)、重心位移距离L计算式[39]为

式中,x i,y i(i=1,2,…,n)为海湾平面离散点的坐标；x j,y j为j时相重心坐标；x k,y k为k时相重心坐标。

1.3.5 岸线分形维数

Mandelbrot于20世纪60年代创立了分形理论[40],之后,该理论得到了广泛应用。由于分形维数不随尺度的变化而变化,因此它能较精确地反映岸线形态的弯曲与复杂程度。分形维数越高,岸线的弯曲度与复杂度就越高。岸线分形维数的计算通常采用2种方法:网格法和量规法。

1)网格法

网格法的计算式[26]为

式中,r为网格长度,N(r)为网格数目,A为常数,D为岸线分形维数。

参照航空摄影测量内业规范中的规定[41],本文采用的比例尺分母(Q)为10 000,15 000,25 000,30 000,35 000,50 000,60 000,75 000,90 000和100 000,依据网格的边长转换模型(r=0.3×Q/1 000)[42],计算获得比例尺对应的网格边长分别为3.0,4.5,7.5,9.0,10.5,15.0,18.0,22.5,27.0和30.0 m。

2)量规法

前人[17,43]应用量规法测量海岸线分维没有实现自动化,均采用传统的手工作业进行量算。尽管精度较高,但工作量大,费时费力。本文利用Matlab中的编程模块实现了输入不同的尺子r值,能输出相应的线段数N以及岸线长度L的功能,极大地提高了工作效率。基于此,采用与网格法相同的尺子长度和计算式来计算岸线的量规维。

2 结果与讨论

2.1 海岸线变迁分析

2.1.1 海岸线总体变迁情况

1976—2016年9个时期的芝罘湾海岸线长度和海湾面积变化情况见图2和表3,统计结果表明:1)近40 a来芝罘湾海岸线长度总体呈不断增长的趋势,其中岸线长度自1976—2011年持续增加,仅在2011—2016年略有缩短。1976—2016年海岸线长度整体增加了15.78 km,较1976年,2016年岸线长度增加了66.17%,年均增加0.39 km,说明芝罘湾海岸线受到人为开发活动的强烈影响。1976—1981年、1981—1986年、1991—1996年和2006—2011年四个时段岸线长度增长较快,变化百分比介于7.24%～16.24%,其中以1976—1981年长度增加最快,变化百分比为16.24%；1986—1991 年、1996—2001 年、2001—2006 年、2011—2016年四个时段岸线变化较慢,其中1996—2001年仅增加了0.48 km,变化百分比仅为1.35%,2011—2016年间海岸线长度减少了0.49 km,变化百分比为-1.21%,海岸线长度变化速率呈现不均衡性的特点。2)近40 a来,芝罘湾海湾面积由1976年的34.16 km2减少至2016年的26.23 km2,面积减少了23.21%,年均面积减少了0.20 km2,总体上呈不断减小趋势。芝罘湾海岸整体保持向海前进的趋势,向陆后退的区域较少,只有南岸烟台山至东炮台岸段的砂质岸线因侵蚀作用有相对明显的向陆后退现象。1981—1986年和1996—2001年海湾面积变化较大,其面积分别减少了1.72和1.70 km2,变化率均为-0.34 km2/a；而2001—2006年和2011—2016年海湾面积变化较小,分别减少了0.21和0.26 km2,变化率分别为-0.04和-0.05 km2/a,所以,海湾面积变化呈现时间和空间变化不均衡性。

图2 芝罘湾1976—2016年海岸线长度及海湾面积Fig.2 Changes of the coastline length and bay area of the Zhifu Bay from 1976 to 2016

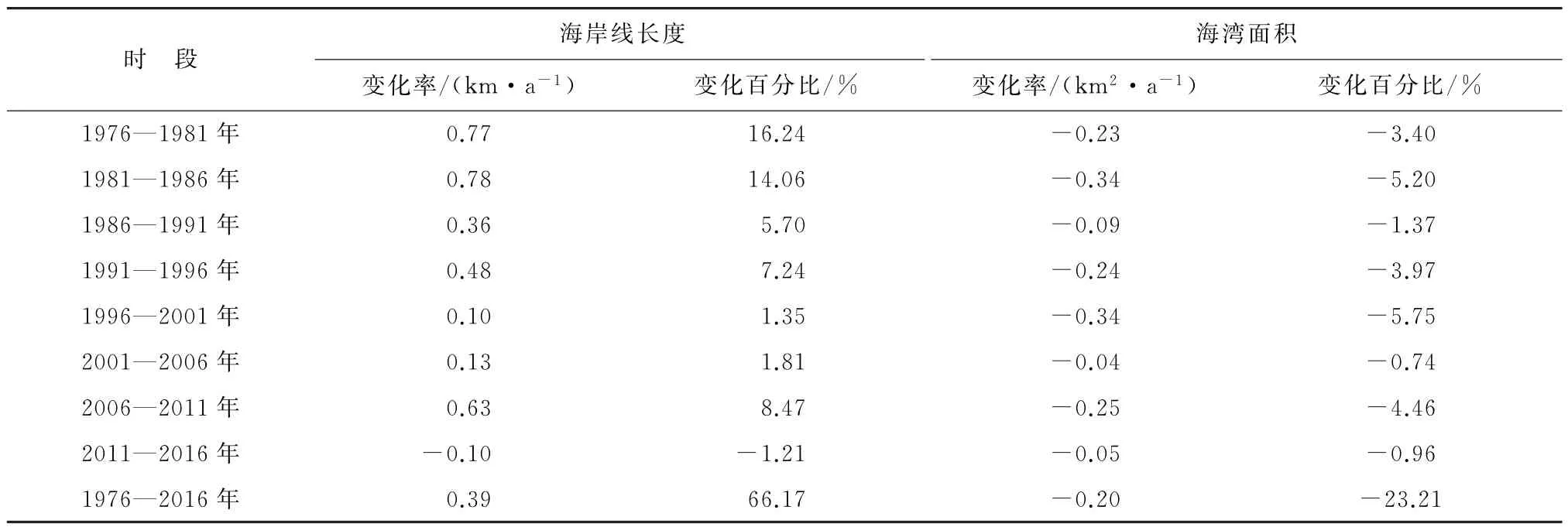
表3 芝罘湾1976—2016年海岸线长度、面积变化情况Table3 The changes of coastline length and bay area of the Zhifu Bay from 1976 to 2016

整体上,芝罘湾自然岸线长度和比例显著减少,而人工岸线迅速增加(图3a)。1976—2016年,自然岸线长度由13.58 km减少至5.10 km,比例由56.93%减少至12.88%,人工岸线长度由10.27 km增长至34.52 km,比例由43.07%增加至87.12%。40 a间自然岸线长度减少了8.48 km,年均减少接近200 m；人工岸线长度增加了25.25 km,年均增加约600 m。其中,以1976—1981年岸线长度变化最为显著,自然岸线长度减少3.68 km的同时,人工岸线长度增加了7.55 km；其次为1981—1986年和1991—1996年两个时段岸线(自然岸线长度分别减少了1.94和1.68 km,其人工岸线长度分别增加了5.84和4.09 km)。

2.1.2 海岸线变迁分段研究

芝罘湾北岸主要岸线类型变化见图3b,岸线长度整体呈现增加趋势,由1976年的6.51 km增加到2016年的11.21 km,年均增长0.12 km。其中1991—1996年岸线缩短,1996—2006年岸线基本稳定,其他时段岸线呈现增加趋势,但增速缓慢。

图3 1976—2016年芝罘湾岸线分类变化Fig.3 Changes of the coastline types in the Zhifu Bay from 1976 to 2016

自然岸线的长度和比例逐渐降低,由1976年的2.24 km(34.42%)下降至2016年的0.92 km(8.21%),岸线长度减少了近60%,而人工岸线的长度和比例却增长较快,由1976年的4.27 km(65.58%)上升至2016年的10.29 km(91.79%),岸线长度增加了近1.4倍。近40 a来,自然岸线长度减少了1.32 km,年均减少约35 m；人工岸线长度增加了6.02 km,年均增加约150 m。

芝罘湾西岸主要岸类型变化见图3c,岸线长度整体增加,由1976年的10.43 km增加到2016年的19.64 km,年均增长0.23 km。其中1976—2011年岸线长度整体增加,仅有2011—2016年波动减少,岸线变化显著,与芝罘湾整体岸线长度的变化趋势基本一致；1991—1996年岸线长度增速最快,年均增长0.56 km,1996—2001年岸线长度增速最慢,年均增长0.10 km,2011—2016年岸线缩短,年均减少0.19 km,减小趋势不均衡。自然岸线的长度和比例迅速降低,由1976年的6.98 km(66.91%)下降至2016年的1.78 km(9.05%),岸线长度减少了近75%,而人工岸线的长度和比例却增长较快,由1976年的3.45 km(33.09%)上升至2016年的17.86 km(90.95%),岸线长度增加了近4.2倍。近40 a来,自然岸线长度减少了5.20 km,年均减少130 m；人工岸线长度增加了14.41 km,年均增加360 m。

芝罘湾南岸主要岸线类型变化见图3d,岸线长度变化相对较小(图3d),由1976年的6.91 km增加到2016年的8.78 km,年均增长0.05 km。其中岸线长度自1976—1996年整体持续增加,且1981—1986年岸线长度增速最快,年均增长0.15 km,至1996年以后岸线基本保持稳定。自然岸线的长度和比例逐渐降低,由1976年的4.36 km(63.06%)下降至2016年的2.41 km(27.42%),岸线长度减少了近45%,而人工岸线的长度和比例却增长较快,由1976年的2.55 km(36.94%)上升至2016年的6.37 km(72.58%),岸线长度增加了近1.5倍。近40 a来,自然岸线长度减少了1.95 km,年均减少约50 m；人工岸线长度增加了3.82 km,年均增加约100 m。

2.2 海湾形状指数时空动态分析

由各个时相的海湾形状指数(图4)可知,2016年芝罘湾海湾形状指数较1976年增加了1.08,整体表现为逐年增加的态势,仅2011—2016年略微减小,这表明海湾的形状总体上趋于复杂化。分时段统计结果表明,1976—1986年和2006—2011年海湾形状指数增长较快,年均增长了0.05；而2011—2016年海湾形状指数略微减小,减少了0.01。海湾形状指数的增大主要是由于以围填海为主要特征的岸线变化提高了海湾形状的复杂性。

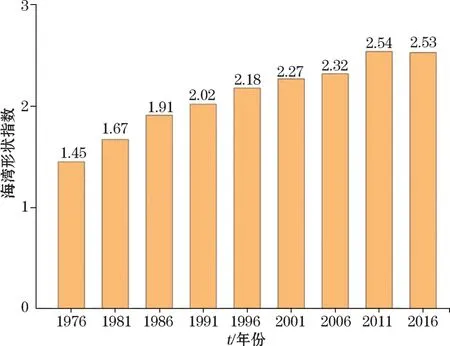
图4 芝罘湾1976—2016年海湾形状指数变化情况Fig.4 Changes of gulf shape index in the Zhifu Bay from 1976 to 2016

2.3 海湾重心位移特征

芝罘湾不同时段重心的位移距离计算结果表明(表4和图5),近40 a来,芝罘湾海湾重心整体向海移动了606.25 m,偏移速率为15.16 m/a,海湾重心处于较为活跃的状态。不同时段海湾重心的位移特征呈显著差异,1996—2001年海湾重心向海移动距离最大为167.57 m,偏移速率为33.51 m/a；其次是1981—1986年,偏移速率为27.30 m/a；1991—1996年偏移速率为20.33 m/a；2011—2016年海湾重心位移最小,向海移动了15.99 m,偏移速率为3.20 m/a。但是海湾重心的位移总体上表现为不断背离陆地而趋向海洋的特点,与围填海所导致的海湾面积的萎缩方向和岸线空间位置的整体移动方向一致。

表4 芝罘湾1976—2016年海湾重心偏移情况Table 4 Gulf-centroid shifting in the Zhifu Bay from 1976 to 2016

图5 芝罘湾1976—2016年海湾重心偏移情况Fig.5 Gulf-centroid shifting in the Zhifu Bay from 1976 to 2016

2.4 岸线分维数时空变化特征

2.4.1 网格法

根据各尺度(r)所对应的网格数目(N),基于ArcGIS中的Arc Toolbox转栅格功能模块,计算获得芝罘湾各时期岸线的分形维数,结果如表5所示。

本文获取的拟合系数(R2)均大于0.999 8,表明拟合获取的分形维数值均精确可用。分维数变化整体呈现增加的趋势,由1976年的1.007 8增加到2016年的1.033 2,增加了2.52%。其中1976—2006年分维数持续增加,2006—2011年略有减小,至2011—2016年保持稳定。这与海岸线长度的变化趋势基本一致,表明随着我国海域使用方式的不断优化和海域使用管理的加强,海岸线的分形维数不断增大,海岸线变得越来越复杂。1981—1986年分维数增幅最大,增长了0.013 7,而2006—2011年分维数则减少了0.002 6。海岸线分维数不同时段出现波动,表明受人为因素影响较大。

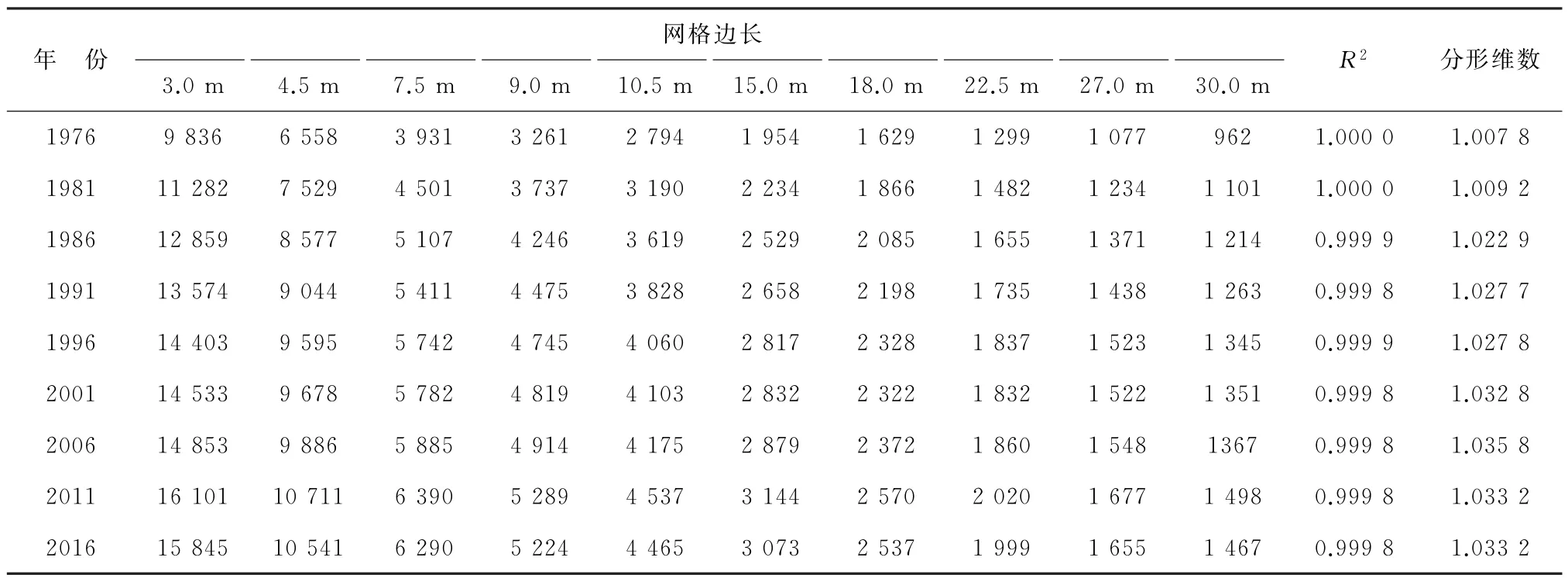
表5 网格法网格数和分形维数Table 5 The fractal dimension of the box-counting method

2.4.2 量规法

量规法的思路是使用不同长度的尺子去度量同一段海岸线,海岸线的长度L(r)由尺子长度r和尺子测量的次数N(r)来决定。尺子的长度越小,测得的海岸线长度越接近被测量海岸线长度的实际值[44]。基于自编的Matlab程序,采用10个量测尺度(r)计算获得芝罘湾各时期岸线的量规维(表6)。

量规法获取的拟合系数(R2)均不低于0.999 9,表明拟合获取的分形维数值均精确可用。分维数变化整体呈现增加的趋势,由1976年的1.016 1增加到2016年的1.034 2,增加了1.78%,仅有2006—2011年分维数变化出现短暂的小幅逆转,由2006年的1.033 9减少到2011年的1.033 0；分维数增幅最大的时段出现在1981—1986年,增长了0.007 6,分维数变化规律与网格法所得结果基本一致,表明海岸线在人为影响下变得越来越复杂。

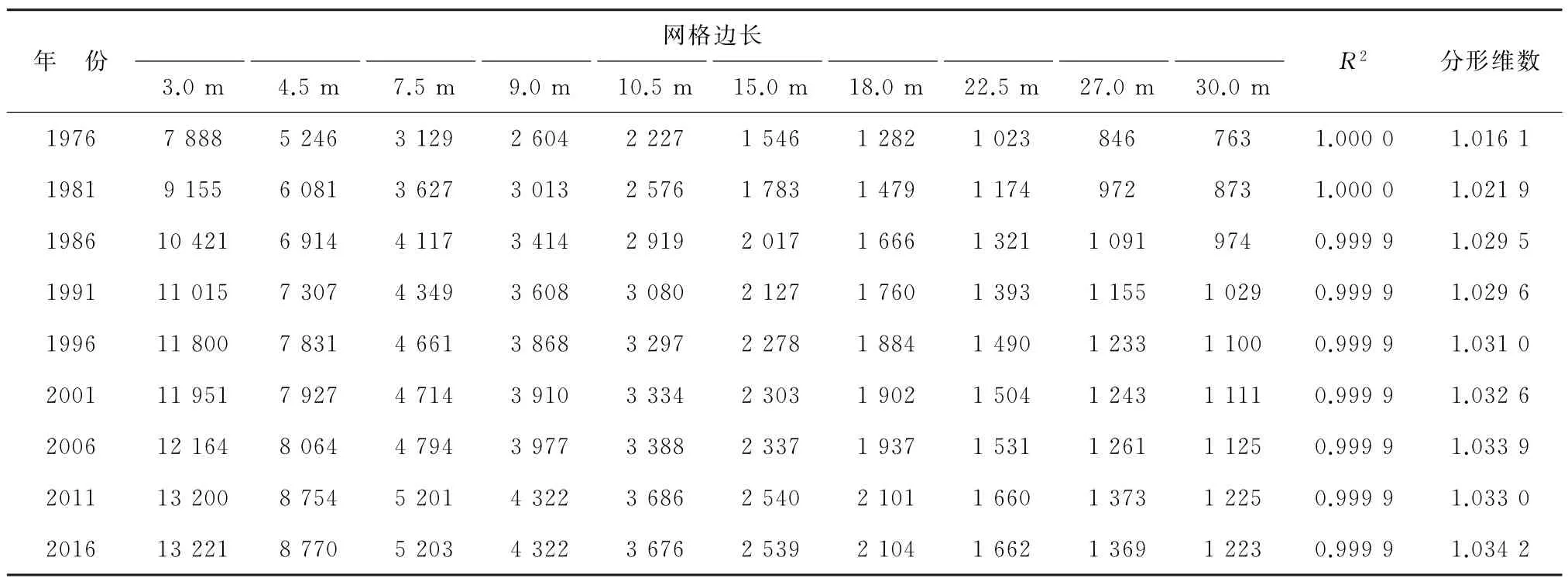
表6 量规法分形维数Table 6 The fractal dimension of the divider method

2.4.3 网格法和量规法分维数对比分析

无论是网格法还是量规法,分形维数的变化规律基本一致,即整体上呈现增大的趋势,其中1981—1986年分维数增幅最大,2006—2011年分维数略有减小,这表明海岸线在这2个时段受人类活动影响比较剧烈。另外,本文只是计算了海岸线整体的分维,没有再分岸段分别计算岸线分维数,实际上每一段岸线内部的不规则程度还存在差异,特别是芝罘湾西部的岸线差异更为明显。如果再细分不同岸段进行分维和长度计算,将更加符合客观实际。

根据前人的研究成果,不同比例尺下,网格法测量的岸线分维数值普遍小于量规法,而量规法比网格法更能准确地表征海岸线的不规则程度[46]。本文中就分形维数而言,2001—2011年网格法的计算结果大于量规法,其他时段均小于量规法(表7,图6),这与前人的研究结果存在一些差异,可能是由于不同比例尺下岸线的曲折程度存在差异以及量规法自动计算程序的误差共同导致的。

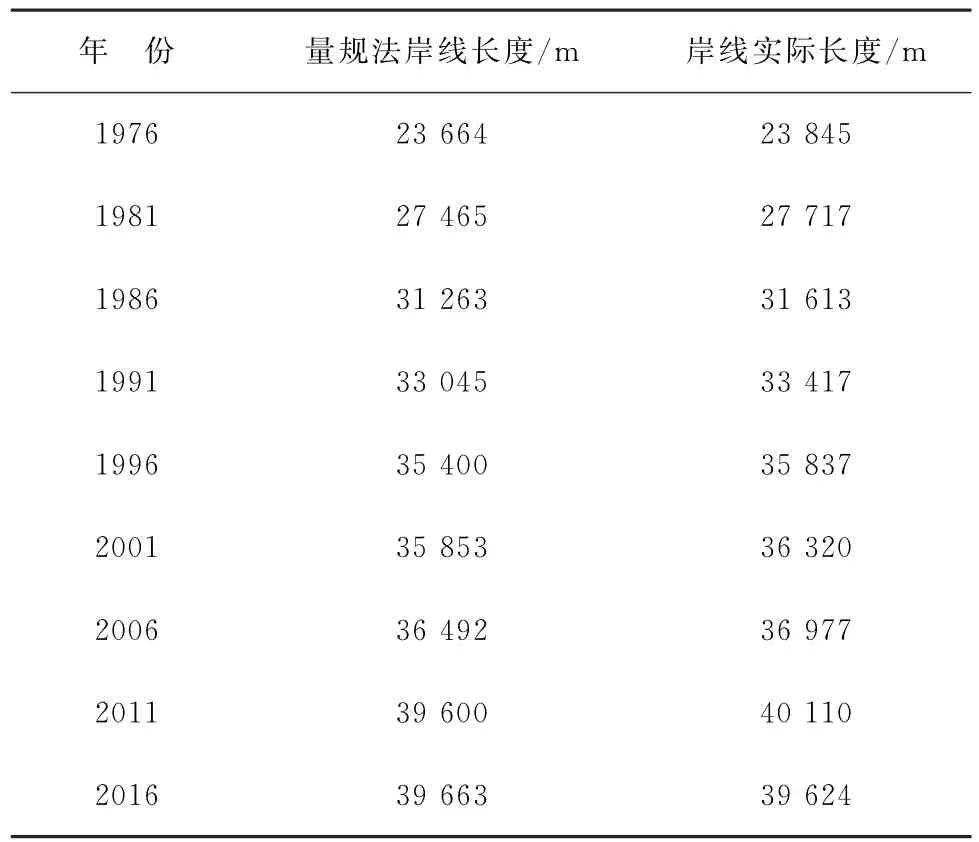
表7 量规法与基于GIS的岸线实际长度对比Table 7 Coastline lengths derived from the divider method and GIS

当尺度r取值为3.0 m时,量规法计算的岸线长度整体小于用ArcGIS统计得出的实际岸线长度(表7),可能受岸线矢量数据离散点的数目影响,也可能是由于Matlab中量规法的实现程序存在一定的误差,程序中只计算了不同标尺r所对应的线段的整数部分,剩余的不足一个标尺r的岸线没有计入最终岸线长度的计算结果,但是作为一种量度方法,Matlab编程算法实现量规法的自动计算,基本满足研究需求,且极大地提高了工作效率。

图6 量规法和网格法分维数Fig.6 The fractal dimension by the divider and box-counting method

2.5 岸线变迁原因分析

近40 a来,芝罘湾岸线的时空变化是自然因素和人类活动共同作用的结果,但是从岸线主要类型变化以及海湾面积的变化特征可以看出,以围填海为主的人类活动是导致岸线变迁的主要因素。

整体来讲,1976—1986年、1991—2001年、2006—2011年芝罘湾岸线变化较为显著。这主要是经济和社会因素共同作用的结果。自1978年改革开放以来,随着近海水生生物养殖业的迅速发展,海水养殖区的面积不断扩大,从而使得海湾面积大幅减少,人工岸线比例也随之增大。1990年以后,海湾岸线开发进程逐渐加快,芝罘连岛沙坝东侧港口及城镇建设等,导致围填海面积日益增加。至2004年,国家修订了《中华人民共和国土地管理法》,开始实行国有土地有偿使用制度,围填海造地因成本低廉、经济收益大而成为沿海地区解决土地瓶颈的便捷方式。“十一五”计划以来,烟台市贯彻海洋经济发展规划的要求,着力发展港口及滨海旅游业等海洋产业,使得围填海规模进一步扩大,至2009年出现围填海面积的激增。因此,2010年国家海洋局开始对围填海实行指标化,此后围填海的热潮开始消退。

分岸段研究结果表明,芝罘湾西岸岸线变化最显著,北岸变化次之,南岸变化最小。西岸岸线的变化主要是烟台港等港口码头堤坝的建设活动造成的；北岸岸线的变化主要源于填海造陆以及围海修建养殖堤坝；而南岸,由于烟台山至东炮台岸段存在较为稳定的自然岸线,变化相对较小,引起变化的原因主要是建设海水浴场和其他旅游设施。

3 结 论

利用遥感和GIS技术提取了芝罘湾1976—2016年9个时相的海岸线信息,并从5个方面分析了芝罘湾岸线的时空动态特征,得到主要结论:

1)海岸线长度整体增加,而海湾面积却整体减少。1976—2016年的40 a间芝罘湾海岸线在人为和自然因素的综合作用下整体向海推进,海岸线长度整体增加了15.78 km。各时段、各岸段海岸线年均变化不均衡,波动较大,其中西岸变化最大,南岸变化最小。岸线结构变化显著,自然岸线比例持续减少,人工岸线逐渐占据主导地位。分形维数整体增大,表明岸线趋于复杂化。而海湾面积逐渐向海萎缩,自1976年到2016年海湾面积减少了7.93 km2,海湾面积的减少主要受近岸养殖以及港口建设等因素的影响。

2)1976—2016年芝罘湾海湾形状指数增加了1.08,海湾形状整体趋于复杂化,海湾重心总体上表现为不断背离陆地而趋向海洋的特点,与围填海所导致的海湾面积的萎缩方向和岸线空间位置的整体移动方向一致。近40 a来海湾重心整体向海偏移了606.25 m,各时段海湾重心偏移速率波动较大。