基于盒维数的水系分维值估算

郑 楠 炯

(广东省水利电力勘测设计研究院，广州 510635)

经典几何图形维数是整数的，1967年曼德尔布罗特(B B Mandelbrot)在研究“英国的海岸线有多长”的问题时，发现海岸线图形面积的有限性而随着测量精度的提高其长度的无限增大性，维数介于1～2之间[1]，从而开创了分形(Fractal)几何学[2]。分形对象具有自相似性和标度不变性两个特征，分形学描述了自然复杂几何体的内在规律，广泛运用到地貌学、物理学、化学和生物学等不同学科研究中。分维数有Hausdorff维数、信息维数、盒维数等多种定义，其中盒维数在所有学科测量中运用最广[3]，适用于自相似的形状，也适用于非自相似的形状，甚至适用于高维空间的对象[4]。

河流水系具有分形特征，分维值反映了河流的复杂程度，分维值越大，水系发育越成熟，水系的复杂度和密集度越高[5-9]。何隆华等[10]根据水系分维数将流域地貌发育阶段划分为3个时期：幼年期、壮年期和老年期，王玉成等[11]计算不同时期水系分维值以研究水系演化过程，小流域早期发育活跃，分维值增大，后期流域趋于稳定，分维值稍有减小；白玉川等[12]研究表明小尺度的分形维数主要反映河弯的发育情况，大尺度的分形特征则反映流域地形的不规则性，朱晓华等[13,14]统计并比较中国各流域水系分维值，大陆水系维数值为1.416 9，其值在平原地区比较大，在山地丘陵区相对较小；Dombrdi等[15]分析地形空间变异与水系分维值的关系，研究表明抬升地形，分维值较大，下陷地形则分维值较小，马宗伟等[16,17]研究长江中下游和赣江流域水系分形特征与径流的关系，分维值越高，河网密集，调蓄能力越强，洪涝干旱灾害的可能性越低。

水系分维值的盒维数法计算研究中，有学者以一定比例尺的实际河网扫描图作为底图计算分维值[10,18,19]，有学者利用DEM提取数字河网作为底图计算分维值，其中有选择不同精度的DEM源[20～24]，有不同汇流阈值的确定方法，如以河网密度-阈值关系变化趋势确定[25-27]，以分维值-阈值关系变化趋势确定[28,29]，或选择与实际河网比较符合时的数字河网的阈值[30]。

本文利用Arcgis平台基于两种精度DEM提取华南地区泗合水流域河网和韩江流域及其子流域河网，采用盒维数法计算系列阈值下的可能水系分维值，并与实际河网计算的分维值比较，探讨不同DEM精度、汇流阈值、河网图源、子流域划分及流域面积对盒维数法计算水系分维值的影响，为水系分维值的盒维数法计算研究提供参考。

1 研究区域概况

1.1 泗合水流域

泗合水流域位于广东省珠江三角洲西部的潭江支流，东经112°22′～112°37′，北纬22°32′～ 22°45′。流域集水面积131 km2，干流总长度26 km，河床比降0.281%，属于亚热带季风气候，多年平均降雨量1 696 mm，多年平均蒸发量868 mm。地形以丘陵为主，200 m高程以下占93.8%。土地覆被为多树草地、作物地等，以人工经济林为主。

1.2 韩江流域

韩江流域覆盖广东东部、福建西南部、江西东南部，包含汀江、梅江、韩江等，东经115°13′～117°09′、北纬23°17′～26°05′。流域集水面积30 112 km2，干流总长度428 km，河床平均比降0.039%，属亚热带季风气候，多年平均降雨量1 407～2 143 mm，多年平均蒸发量996～1 406 mm。地势自西北和东北向东南倾斜，丘陵与谷地相间，山地占总流域面积的70%。山地丘陵的植被是以马尾松为主的次生林地，台地、盆地和平原多为农作物。考虑三角洲数字河网提取的不准确性，本文研究的韩江流域不包含潮安水文站以下的沿海三角洲区域(集水面积1 035 km2)，研究区域地理位置见图1。

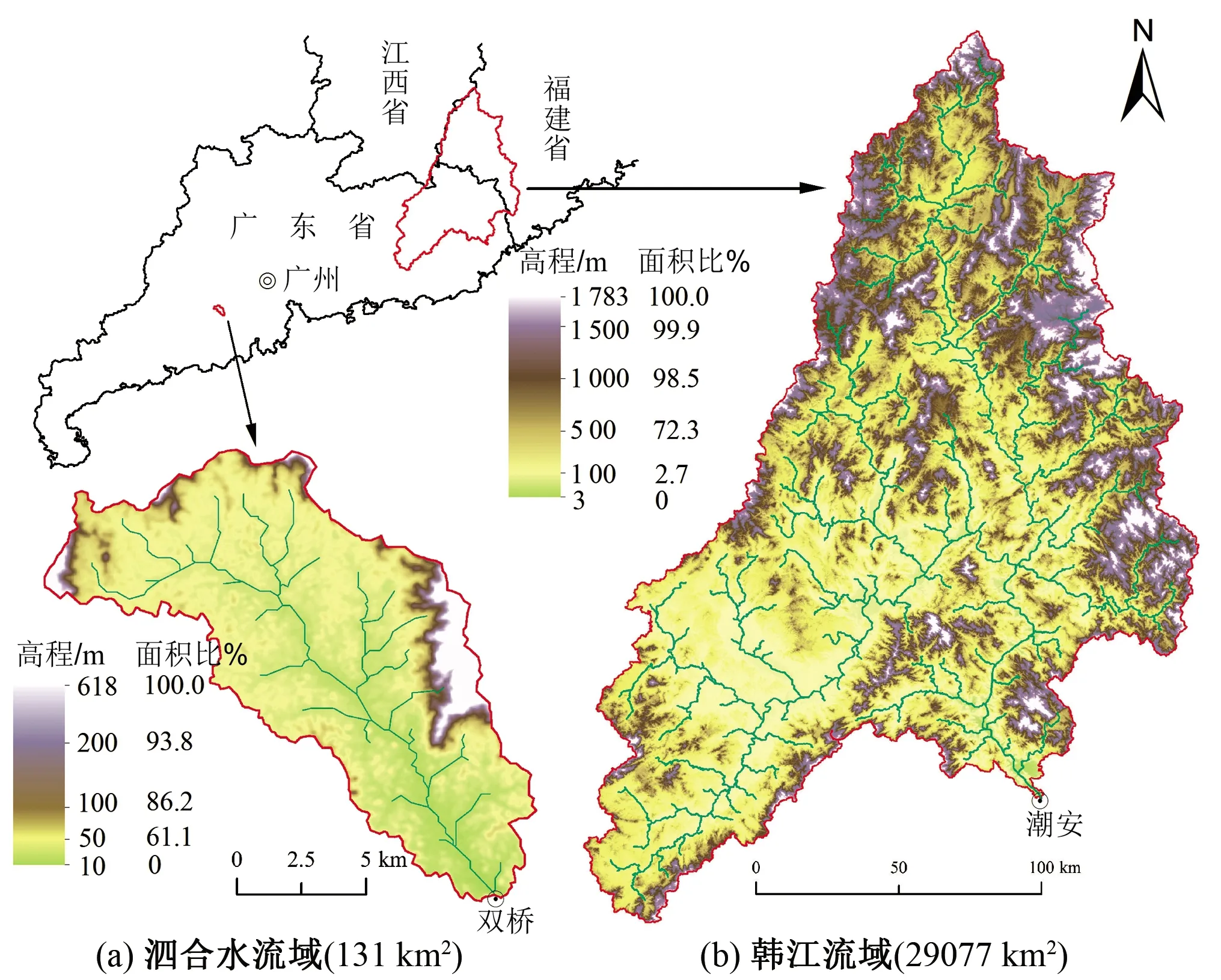
图1 研究区域地理位置及高程分布Fig.1 Geographical location and elevation distribution of the study areas

2 研究方法

2.1 流域水系的提取

研究模型的是利用DEM(Digital Elevation Model，数字高程模型)提取矢量河网，进行分维分析。DEM数据来源一般有影像测量、地面测量、已有地形图数字化等几种途径。本文的DEM数据采用中国科学院计算机网络信息中心的地理空间数据云(http:∥www.gscloud.cn)提供的两种分辨率的DEM：分辨率90 m的SRTM DEM和分辨率30 m的GDEM DEM。SRTM DEM(航天飞机雷达地形测量)水平分辨率为90 m，标称绝地高程精度是±16 m，置信度为90%，标称绝对平面精度是±20 m；ASTER GDEM(先进星载热发射和反射辐射仪全球数字高程模型)水平分辨率为30 m，垂直精度是±20 m，水平精度是±30 m，置信度为95%。

采用Arcgis平台的水文分析模块对DEM进行填洼(Fill)、计算汇流方向(Flow Direction)、生成汇流栅格(Flow Accumulation)、确定流域边界(Watershed)和提取数字河网(Stream to Feature)等，泗合水流域以双桥水文站(112°35′21″，22°34′32″)为流域出口点，韩江流域以潮安水文站(116°39′0″E，23°40′0″N)为流域出口点，生成两种精度的数字河网[31]。

不同的汇流阈值生成疏密不同的河网，多尺度汇流量阈值下的水系分维值更精确[32]，汇流栅格阈值的确定采用枚举法，汇流网格单元数从最小值1逐渐增大到提取的河网十分粗糙为止，如汇流面积阈值5 km2(面积阈值=单元格面积×栅格数阈值)，得到一系列不同密集度的河网，用于分析阈值与水系分维值的关系。

2.2 盒维数法

盒维数反映了物体对空间填充的程度，具有统计意义上的分形特征，反映河网的复杂程度，分维值越大，河网越复杂。河网越密集，河网落在分形盒子的几率更大，相应计算出的分维值越大。盒维数法是用相同网格去覆盖分形对象，统计网格尺寸和所覆盖的网格数量，计算过程只考虑图形的分布，计算简单和方便，是应用最广的维数之一。

对于不是自相似的结构，比如流域水系，将分形对象分别置于不同网格尺寸s的网络中，相应分形对象包含的网格数目N(s)。

N(s)∝s-D

(1)

双对数图中用一条直线去拟合系列点[s，N(s)]，该直线的斜率的绝对值即为对象的分维值D[1]。

lgN(s)=-Dlgs+C

(2)

式中：D为分维值；s为网格边长；N(s)为网格数；C为待定常数。

分形对象具有自相似性，物体的任何小部分与整体相似，分形对象不具有特征长度，即无标度区间，盒维数法系列网格边长就是无标度区间，为了使数据对在对数坐标系统的横坐标方向上是均匀分布，一般网格的边长取为[33]：

si=2is0,i=1,2,…,n

(3)

式中：s0为最小的网格单元边长。

本文最小网格单元边长取10，无标度区间取[10，20，30，50，100，150，…，500，800，1 000]，研究的流域水系在该区间内表现出较好的分形特征，相关系数在0.97以上。

2.3 模型的建立

Arcgis平台下，设置不同的阈值提取数字河网，再栅格化(Feature to Raster)，转换成不同网格单元大小(s)的栅格图，此过程等同于盒维数法的盒子覆盖(图2)，统计栅格数目[N(s)]，对s和N(s)进行线性回归分析，斜率的绝对值即为分维值。利用Arcgis平台的模型构建器(ModelBuilder)建模(图3)，实现批量化处理及结果输出，避免了重复性人工操作并提高了计算效率。

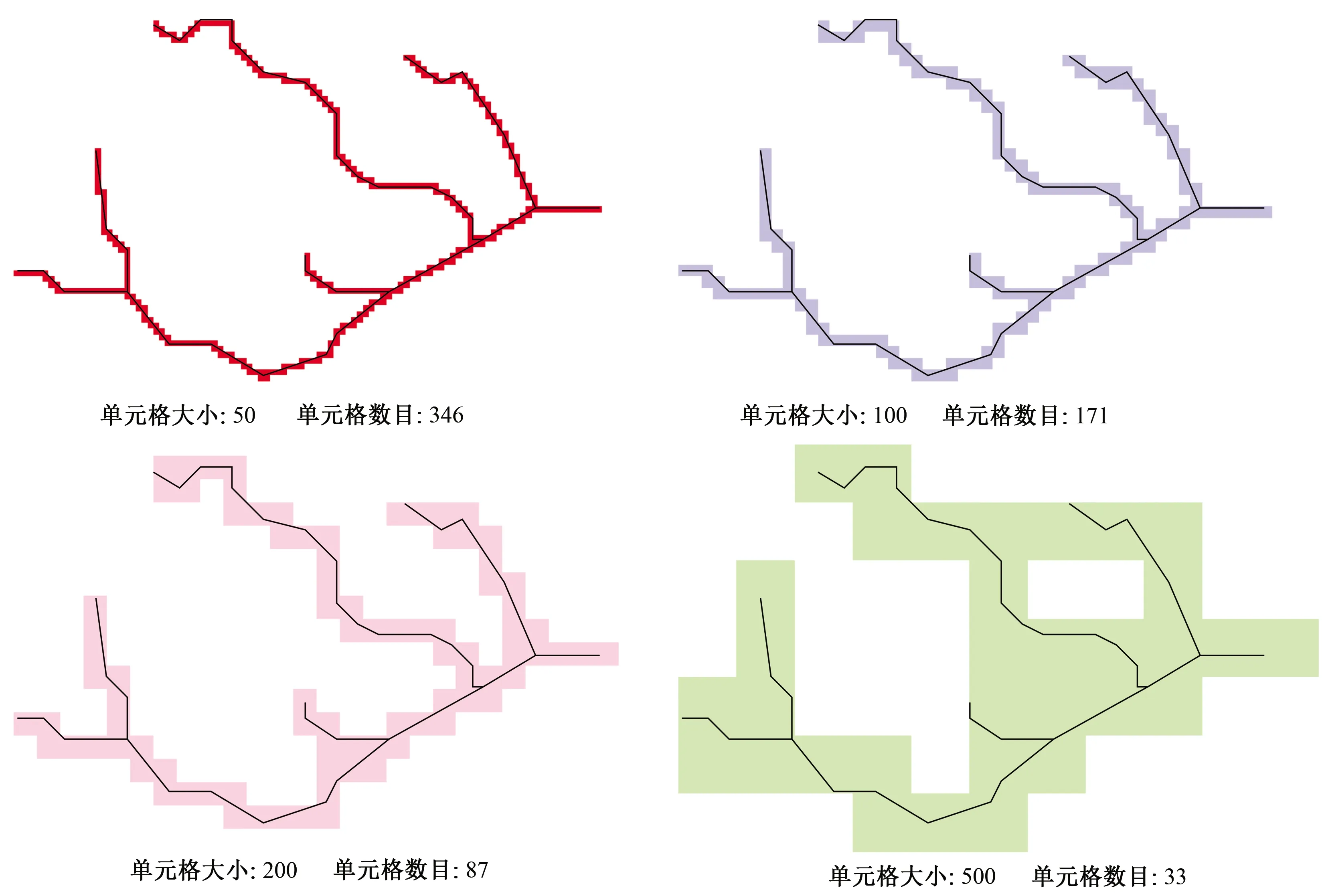
图2 矢量河网栅格化成不同边长的网格图Fig.2 River network gridding with different side lengths

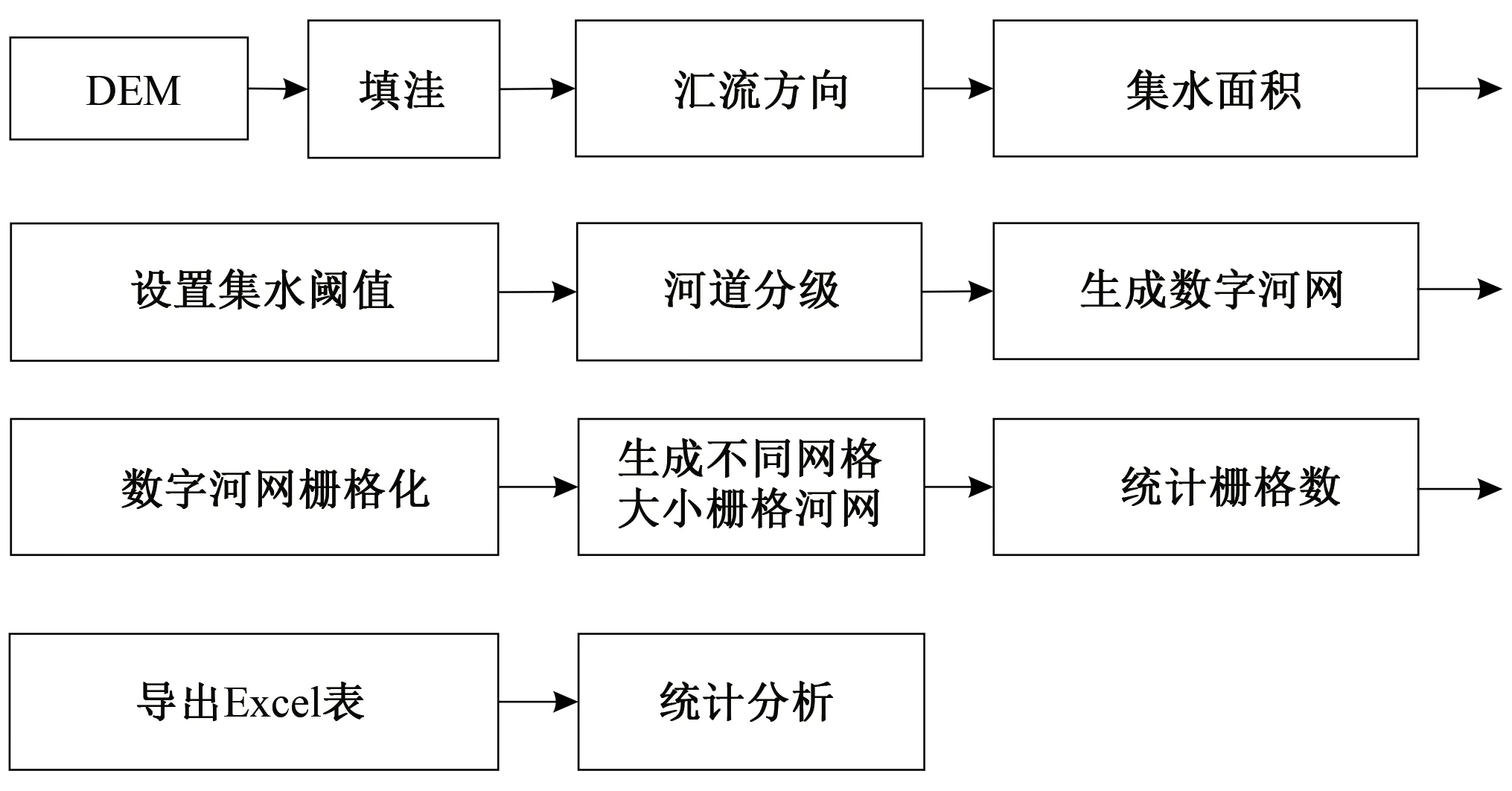
图3 计算水系分维值流程图Fig.3 Flow chart of calculating drainage fractal dimension

3 结果与分析

3.1 流域水系分维值

提取泗合水流域和韩江流域两种DEM精度的数字河网，提取的数字流域面积与实际流域面积接近，但存在一定的误差(见表1)，这与DEM的精度以及河网提取方法等有关。

表1 泗合水流域和韩江流域面积对比Tab.1 Area comparison of Siheshui basin and Hanjiang River basin

泗合水和韩江流域部分汇流阈值的河网的分维值D和s与N(s)线性回归分析的相关系数R2列于表2。泗合水流域R2大于0.98，韩江流域R2大于0.97，s与N(s)拟合相关性好，研究的水系分别在无标度区间内统计自相似，表现出较好的分形特征。

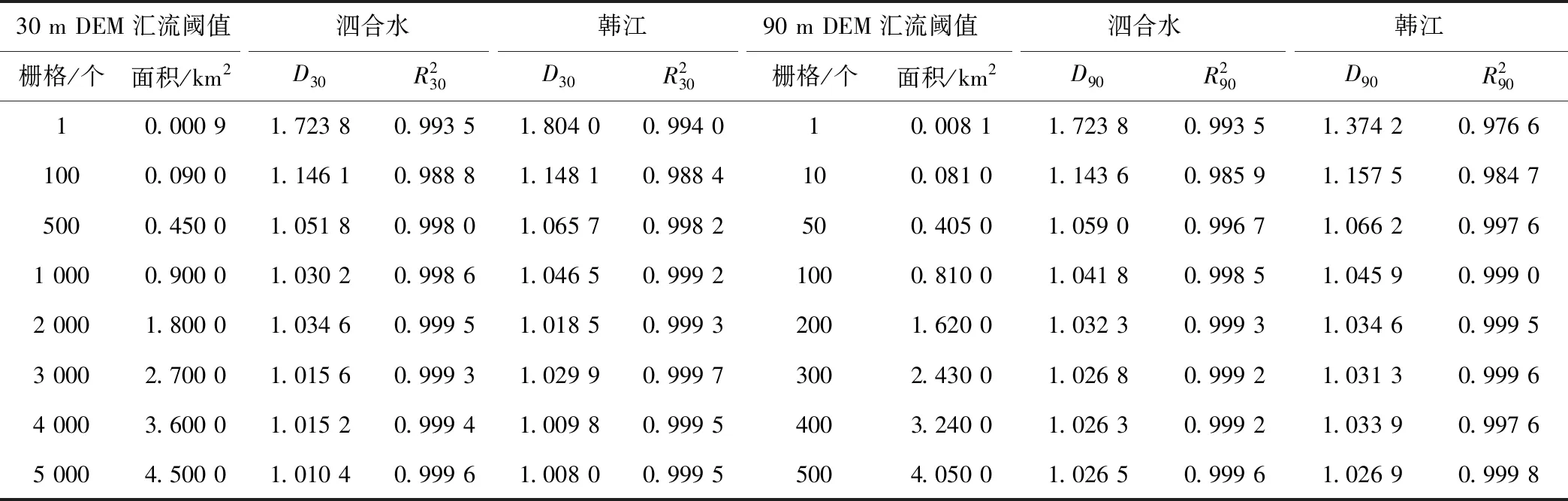
表2 泗合水和韩江流域在部分汇流阈值下的水系分维值和相关系数Tab.2 Drainage fractal dimension and the correlation coefficient in some conflux threshold values of Siheshui basin and Hanjiang River basin

枚举汇流阈值，得到流域可能的系列水系分维值，见图4。

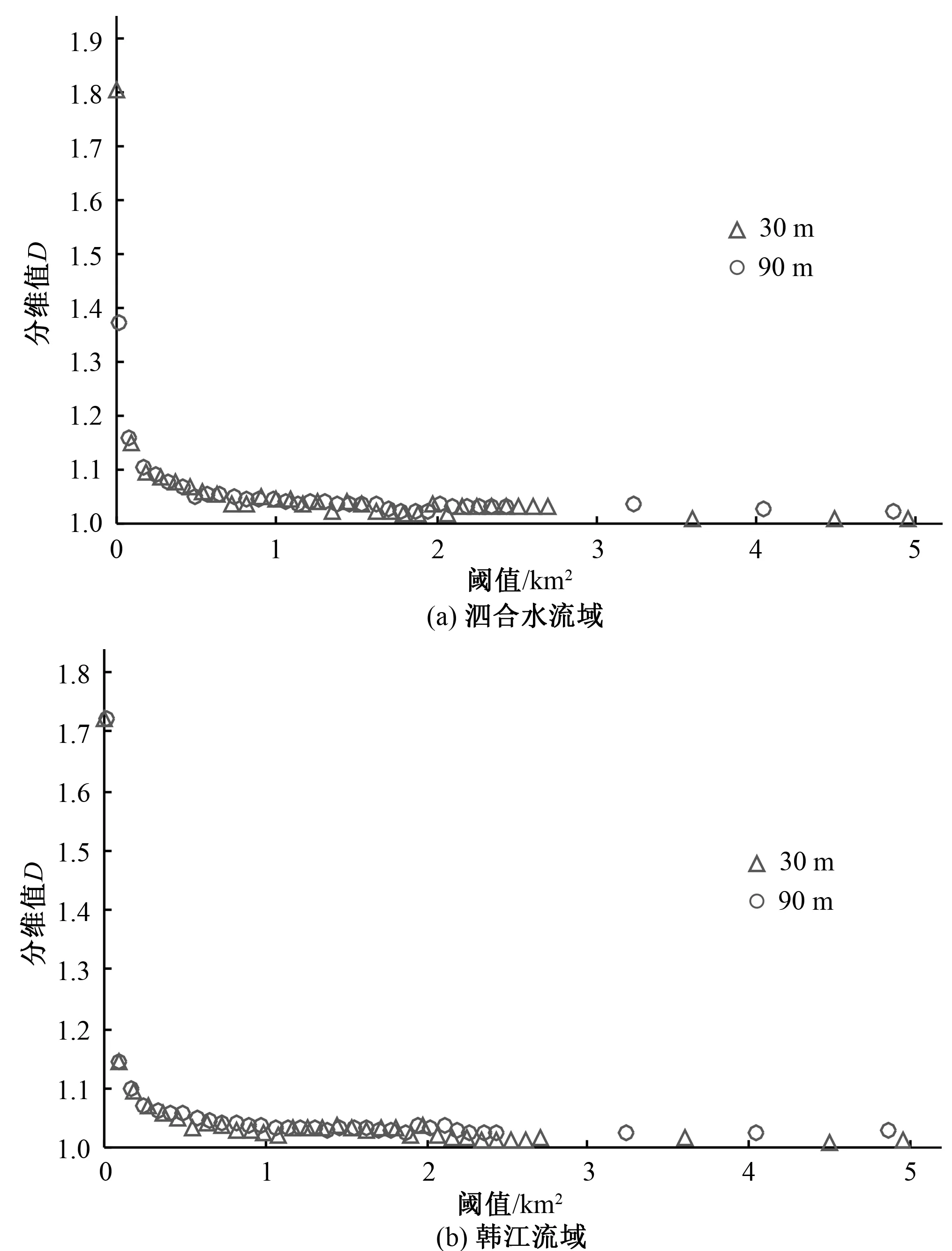
图4 泗合水流域和韩江流域系列水系分维值Tab.4 Series of drainage fractal dimension of Siheshui basin and Hanjiang River basin

3.2 DEM分辨率对盒维数法计算分维值的影响

不同DEM源由于水平精度和垂直精度的差异，提取的流域及河网信息存在差别，刘远等[34]研究表明，90m精度的SRTMDEM提取的河网精度较高。由图4，在不考虑河网精度的前提下，泗合水流域和韩江流域分别基于两种DEM计算的流域水系分维值较为接近，且有着相同的变化趋势。韩江流域在汇流栅格数阈值为1时两种DEM计算的分维值差别较大，这是由于最小汇流面积阈值不同造成河网密度的不同，30m精度的最小阈值是0.000 9km2，90m精度的是0.008 1km2。在不考虑河网精度的前提下，泗合水流域和韩江流域分别基于两种DEM计算的流域水系分维值较为接近，且有着相同的变化趋势。因此，基于两种分辨率DEM对盒维数法计算水系分维值差别不大。

3.3 汇流阈值对盒维数法计算分维值的影响

阈值的确定在河网的提取过程中起着关键性作用，阈值决定提取生成河网的密度和精度，随着设定阈值的增大，河网密度会呈现指数降低的趋势。汇流栅格数取最小值1时，生成的河网最为密集，河网分级最为复杂，水系分维值达到可能最大值，由图4，泗合水流域水系分维值最大是1.723 8，韩江流域水系分维值最大是1.804 0。汇流面积阈值从最小值增加到0.5km2时，泗合水流域和韩江流域分维值骤减，变化明显。随着阈值逐渐增大，水系越稀疏，河网分级结构越简单，趋势线出现一个拐点，分维值变化平缓，逐渐减小至趋于1(大于1)，河网概化变成一维图形，此时分维值与汇流阈值无关，杨锦玲等[35]研究也表明水系分维值随汇流阈值增大而减小的变化关系。选择合理的汇流阈值对盒维数法计算数字河网的分维值至关重要。

3.4 河网图来源对盒维数法计算分维值的影响

实际河网形状是确定的，对应的数字河网是唯一的，水系分维值也是唯一确定的。准确的水系分维值应由实际河网计算求得。以韩江流域为例，课题组已描绘了两种比例尺的韩江流域标准河网(图5)，由于测量的比例尺不同，实际河网也表现出不同的疏密程度，现将标准河网栅格化，统计并进行线形回归分析(图6)。

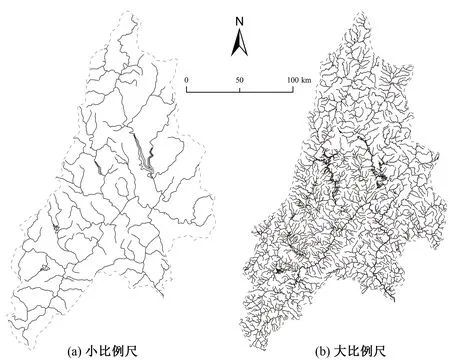
图5 韩江流域不同比例尺实际河网Fig.5 Actual river network of Hanjiang River basin in different scale

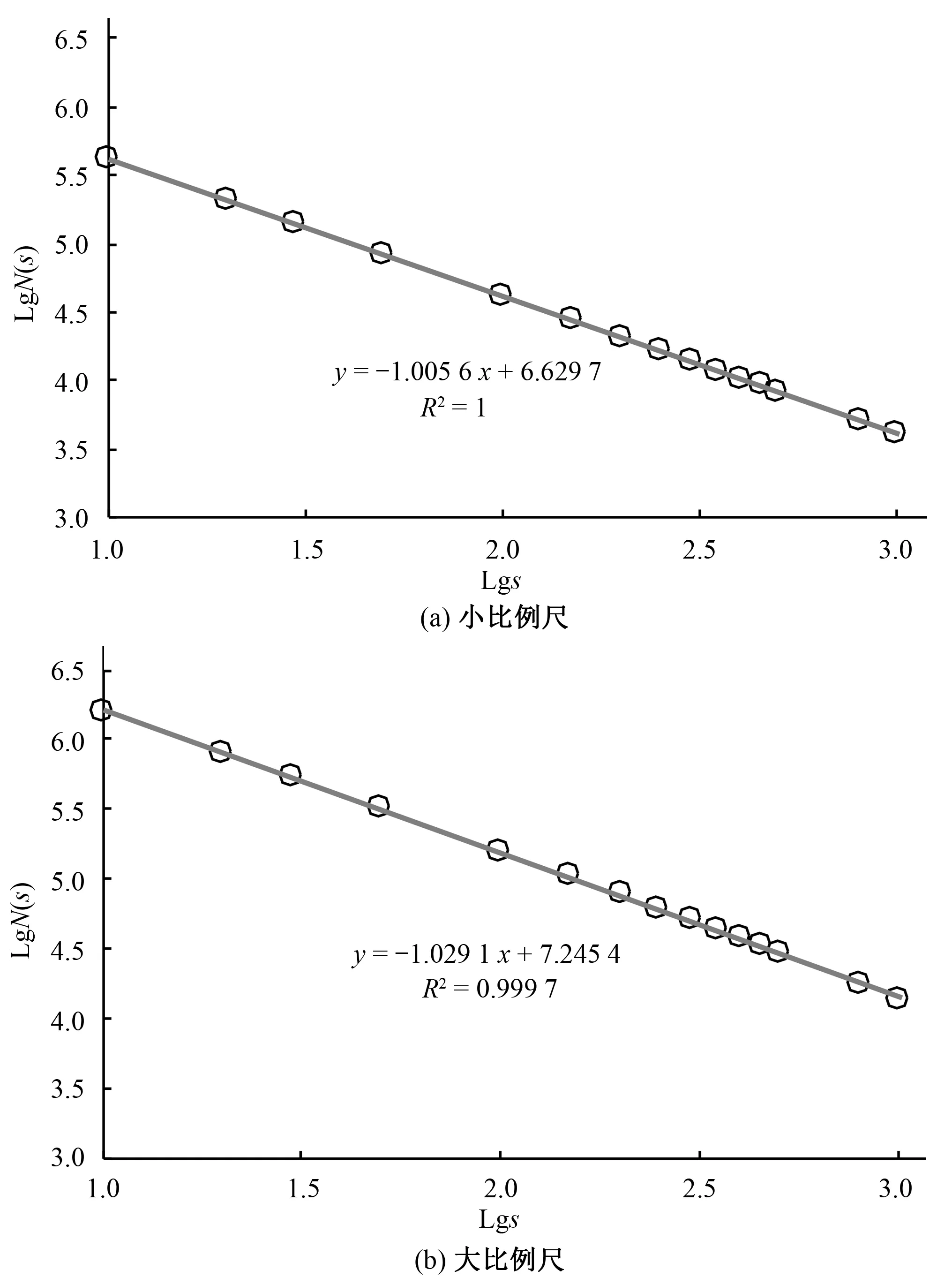
图6 韩江流域大小比例尺下实际河网的s与N(s)的关系曲线Fig.6 Relationship curve between s and N(s) of actual river network of Hanjiang River basin in different scale

由图6，韩江流域小比例尺实际河网的分维值1.005 6，大比例尺分维值1.029 1，二者数值相差不大，大比例尺河网更为细致，分维值比小比例尺的稍大。水系分维值反映了水系的发育程度，韩江流域分维值低，河流发育尚未成熟。对比基于90m的SRTMDEM提取的数字河网，阈值40km2的数字河网与小比例尺河网较为吻合，分维值1.017，相差1.1%；阈值4km2的数字河网与大比例尺河网较为吻合，分维值1.026 9，相差0.2%。汇流阈值是基于DEM提取数字河网的一个重要参数，不同的阈值所提取的河网密度不同，所计算的分维值不同。选择合适的阈值使数字河网与实际河网吻合时，数字河网的水系分维值具有参考意义，一定程度上可以代表实际河网的分维值。

3.5 子流域划分及流域面积对盒维数法计算分维值的影响

前文分析了不同规模流域的分维值(图4)，其中泗合水流域是珠江流域的小流域，韩江流域是广东省除珠江流域以外的第二大流域。不同流域面积的水系均具有分形特征，二者分维值随汇流阈值改变表现出相似的变化规律。

大型水系是一种多重分形[5]，为研究大流域与子流域的分维值关系，将韩江流域内9个水文站点定为流域出口，划分为9个独立的不套合的子流域并以水文站命名子流域。选用SRTMDEM进行韩江子流域分维值的计算分析，韩江子流域划分见图7，整个流域及9个子流域随阈值变化的分维值绘于图8(a)，每个子流域系列分维值取平均值，与流域面积的关系绘于图8(b)。

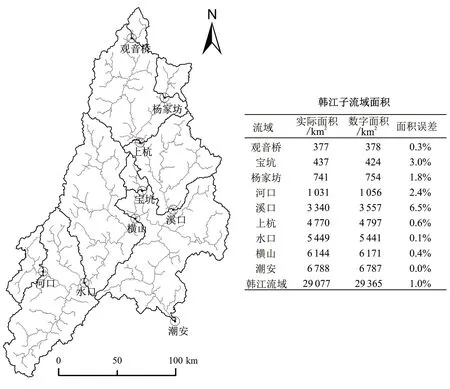
图7 韩江流域水文站点及子流域分布Fig.7 Distribution of hydrologic stations and sub basins in Hanjiang River basin

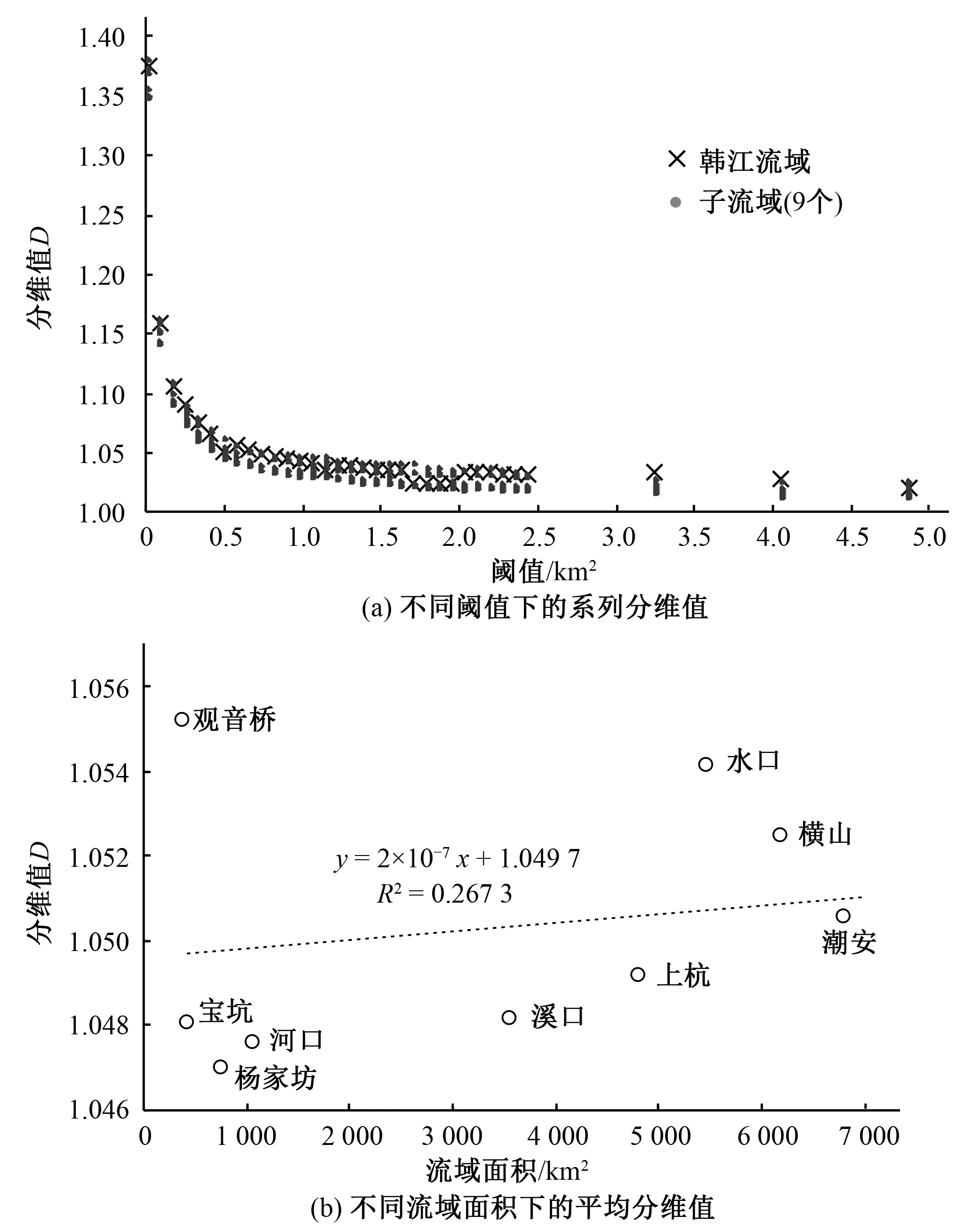
图8 韩江流域的9个子流域分维值Fig.8 Fractal dimension of 9 sub basins in Hanjiang River basin

由图8(a)，如同整个韩江流域，9个不同面积的子流域分维值随汇流阈值增大呈先骤减后平缓减少趋势，同一阈值下各子流域分维值的变差系数皆约0.004，子流域平均分维值范围是1.047 0～1.055 3 ，极差0.008 3，表明各子流域同一阈值的分维值相当。纵向上，整个流域分维值总体比相应阈值下各子流域平均分维值稍大，相差值小于0.012；横向上，韩江流域和子流域系列分维值的平均值分别是1.055、1.050，二者相差0.44%，总体上大流域分维值等于其子流域分维值的平均。不同子流域，流域面积和地形等因素各有差异，分维值相应地稍有不同，其中观音桥流域分维值最大，数字流域面积378km2，位于韩江流域的北部、武夷山脉北麓高丘陵地带，是汀江的发源地，山地穿插，平均高程约650m；水口流域分维值次之，数字流域面积5 441km2，位于韩江流域西南部、武夷山脉南麓低丘陵地带，地势平坦，平均高程约300m；杨家坊流域分维值最小，数字流域面积754km2，位于韩江流域东北部，流域四周山地环绕，内部较平缓，平均高程约600m。线性回归分析分维值与流域面积的关系[图8(b)]，相关系数0.267 3，二者表现不相关，分维值与流域面积大小无关。

综上，流域水系发育均匀，地貌较为一致时，水系具有较强的统计自相似性，同一流域不同面积大小的子流域的水系分维值相近，分形特征明显，分维值与面积无关。

3.6 误差分析

盒维数反映了对象对空间填充的程度，流域水系分维值反映河网的复杂程度，河网越复杂，分维值越大。基于DEM提取河网并计算的水系分维值，受汇流阈值的影响明显。不同汇流阈值的设定，生成不同疏密程度的河网，最终导致河网的分维值浮动。

4 总结与讨论

运用Arcgis平台基于两种精度DEM提取泗合水流域河网和韩江流域及其子流域河网，采用盒维数法计算系列阈值下的水系可能分维值，并与实际河网计算的分维值比较，分析水系分维值与DEM精度、汇流阈值、河网图来源、流域面积的关系，结果表明：

(1)泗合水流域河网的分维值相关系数R2大于0.98，韩江流域R2大于0.97，s与N(s)拟合相关性好，研究的水系分别在无标度区间内统计自相似，表现出较好的分形特征。

(2)不考虑河网精度前提下，基于30和90m分辨率的DEM对盒维数法计算水系分维值影响不大。

(3)基于DEM计算的流域水系分维值受汇流阈值影响，随阈值的增大，分维值骤减后平缓减小至趋于1，有明显的拐点。

(4)准确的水系分维值应由实际河网求得，选择合适的汇流阈值使得数字河网与实际河网吻合时，数字河网的分维值一定程度上可以代表实际河网的分维值。

(5)流域水系发育均匀时，具有较强的统计自相似性，整个流域的水系分维值与流域内的不同子流域水系分维值相近，水系分维值与流域面积无相关关系。

盒维数法计算水系分维值具有不确定性，基于DEM计算时，不同汇流阈值下水系分维值不同；基于实际河网计算时，由于测量比例尺的不同，河网密度不同，也导致水系分维值的差异。利用盒维数计算水系分维值时，提取河网的阈值和标准实际河网的选定需要一个合理的标准。此外，水系分维值是否可以作为单一指标衡量河网的发育程度以及对河网发育程度的定量描述上，有待进一步研究。

□