LSTM和Prophet模型在肺结核发病数预测中的应用

李顺勇， 张钰嘉

（山西大学数学科学学院，太原 030006）

肺结核作为我国重大传染病之一，其发病数的预测已经成为卫生统计领域中一项热门课题［1-3］. 研究肺结核发病数的一种有效方法是对其建立数学模型，不同的数学模型应用到肺结核时序上时，拟合效果也不尽相同. Kermark 提出的SIS（Susceptible-Infected-Susceptible）模型是一种常见的传染病模型，能够较好地描述肺结核传播机制［4］. 传统时间序列模型由于其模型简单易于实现得到了广泛的应用，但其在预测肺结核发病数时会出现滞后性等问题. BP 神经网络通过其较为强大的学习能力建立起了数据之间的非线性关系，在传染病发病数预测方面有一定的优势，但其不能很好地适用于肺结核发病数模型［5-7］. 肺结核发病数的时序中不仅含有线性时序成分，还包括非线性时序，若采用单个预测模型则很难体现出该事件序列的复合特征，因此，不少学者将ARIMA、GM（1，1）、SVR等模型应用到肺结核发病数预测中［8-13］. 2017年，Taylor 等研究人员提出了Prophet模型，该模型支持加入Holiday以及Changepoint，能够弥补传统预测模型（如ARIMA）灵活性、通用性的不足，在肺结核发病数的时序预测方面有较强的鲁棒性［14-15］. Hochreiter 等学者提出了LSTM模型，该模型本质上是RNN模型，该模型在实际应用中能够解决梯度弥散问题，广泛应用于图像处理、自然语言处理、传染病预测中［16］.

本文针对肺结核发病数时间序列数据展开实验，分别利用Prophet模型与LSTM模型对2011—2019年中国肺结核发病数时序数据进行建模，比较两种模型拟合效果以及预测性能，并解释肺结核发病数的规律，掌握该病发展情况，为中国肺结核的防控工作提供依据.

图1 Prophet模型流程图Fig.1 Prophet model flow chart

1 Prophet模型

Prophet 模型是Taylor 等研究人员在2017 年提出的时序模型，该模型能够有效地分析数据本身的特征以及变化规律，并有良好的预测性能. 该模型相较于传统时序模型，加入了Holidays以及Changepoint 因子，预测更加灵活［13］，Prophet 工作流程如图1所示.

Prophet 模型可以理解为加性模型，由growth、seasonality、holidays三个部分组成，模型构成如式（1）所示.

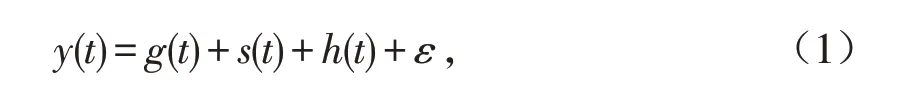
式（1）中：t为时间，g(t)为growth项，是模型的核心项，用来拟合时序中的非周期性变化，该项函数如式（2）所示.

式（2）中：C代表容量；k代表模型的增长率；b代表模型偏移量；t为时间. 可以看出，t增加时，1+e-k(t-b)趋近于1，即g(t)趋近于C.

s(t)为seasonality项，该项使用傅里叶级数代表周期因子，表达式如式（3）所示.

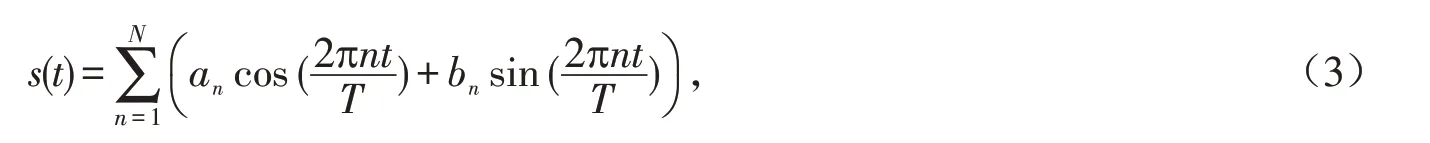
式（3）中：T 代表周期；an，bn是被估参数；t为时间；n代表模型中使用周期数的一半.

h(t)为holidays项，该项将节日影响分成不同的独立模型，表达式如式（4）所示.

式（4）中：每个holiday用i表示；t为时间；Z(t)=[1 (t ∈D1),…,1(t ∈Di)] ，1(t ∈Di)为指示函数，Di为holidays集合，若t在Di中，则1(t ∈Di)的值为1，若t不在Di中，则1(t ∈Di)的值为0；κi为每个holidays 的参数，代表对每个holiday的影响.

2 LSTM模型

LSTM 是循环神经网络（RNN）的一种形式，与RNN 不同的地方在于LSTM 模型增加了Gated，解决了RNN 在层数较多时出现梯度弥散的问题，LSTM 模型在处理肺结核发病数时间序列时有较好的效果［14］. LSTM 模型的关键之处在于三个“门”结构，即Input Gate、Output Gate、Forget Gate，具体组成结构如图2所示.

图2 LSTM组成结构图Fig.2 LSTM model framework

LSTM模型具体计算公式如式（5）～（10）所示.

式（5）～（10）中：it为Input Gate，ot为Output Gate，ft为Forget Gate，c˜t为t时Cell中输入的值，ct为t时Cell中的更新值，ht为储存了t时以及之前隐藏信息的向量；sigmoid，tanh 为激活函数；Wf，Wi，Wc，Wo均为权重矩阵，bf，bi，bc，bo为对应Wf，Wi，Wc，Wo的偏置，具体单元结构图如图3所示.

3 仿真实验

3.1 数据获取

选取2011年7月到2019年9月一共98个月的肺结核发病数作为研究数据，具体内容如表1所示.

根据表1中数据进一步得到肺结核发病数随着时间变化的曲线，如图4所示.

图4的坐标横轴表示98个月份，坐标纵轴为肺结核发病数，从图4可以看出，我国肺结核发病数每月波动较为明显，具有逐年下降的趋势，并且有一定的周期性.

3.2 评价指标选取

为检验LSTM模型以及Prophet模型对肺结核发病数预测的效果，选取MAE以及RMSE两个指标作为评估的标准，指标计算公式如式（11）、式（12）所示.

式（11）～（12）中：x 为肺结核当月发病数的实际值；xˆ为LSTM模型或者Prophet模型的预测值；n 为预测的总月数.

3.3 LSTM模型拟合效果

采用Tensorflow 与Keras 库建立LSTM 模型，该模型有三层，即Input、Output、Hidden 层，模型的epochs 设置为500，单元数设置为128，batch_size设置为1，loss函数设置为mean_squared_error，optimizer设置为adam，train_size设置为数据量的2/3，look_back设置为15，运用LSTM模型对表1中数据进行拟合. 此时，该模型的loss值为6.457 1×10-4，训练集的RMSE值1 439.99，预测集的RMSE值为5 915.26，训练结果如图5所示.

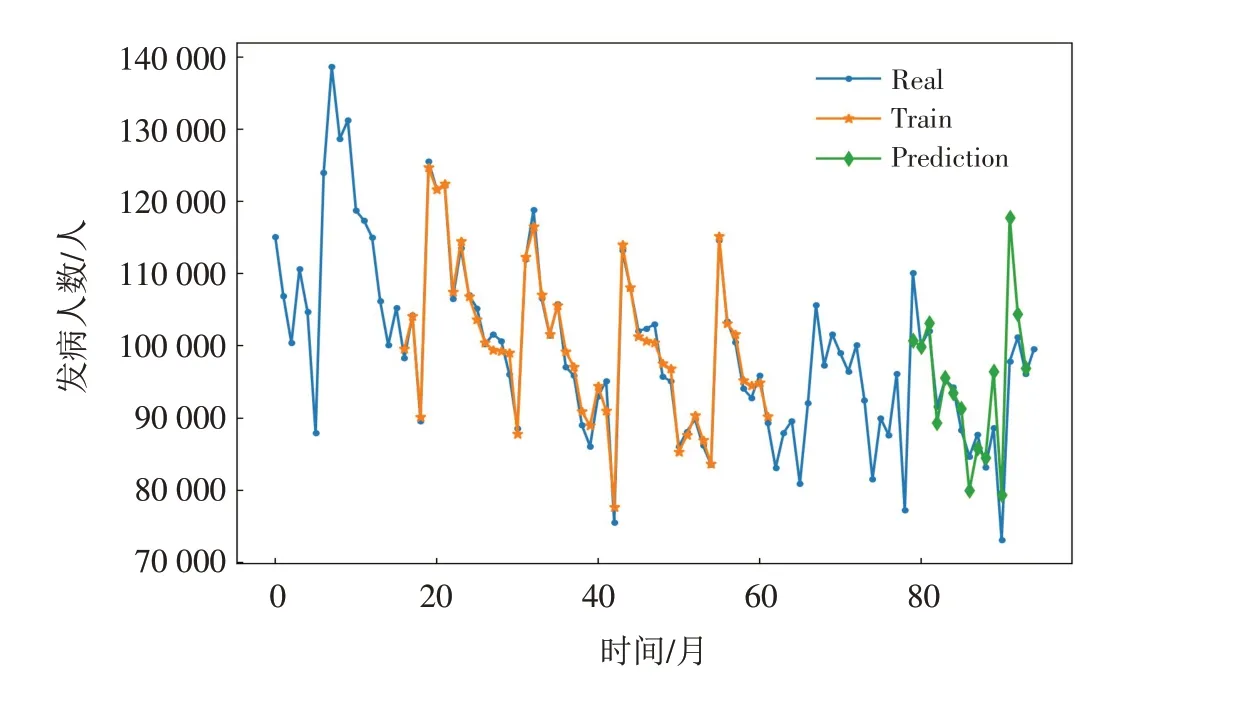
图5 LSTM模型拟合效果Fig.5 LSTM model fitting effect

从图5可以看出，LSTM模型有较好的拟合效果以及预测性能，能够较准确地预测出肺结核发病数的趋势以及人数.

3.4 Prophet模型拟合效果

采用fbprophet库建立Prophet模型，模型的interval_width设置为0.95，periods设置为12，fre设置为MS，运用Prophet模型对表1中的数据进行拟合. 此时，该模型的RMSE值为4 856.66，拟合效果如图6所示.

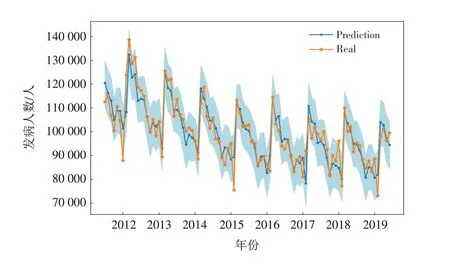
图6 Prophet模型拟合效果Fig.6 Prophet model fitting effect

图6中阴影部分为interval_width 等于0.95时的Prophet模型预测值的上下界. 由图6可知，Prophet模型有较好的拟合效果，预测结果也与实际情况相吻合.

3.5 模型对比

为比较两种模型预测值，运用LSTM模型以及Prophet模型对表1中2007年6月至2018年12月的数据进行训练，并对2019年1月至2019年6月的数据进行预测，预测结果如图7所示.

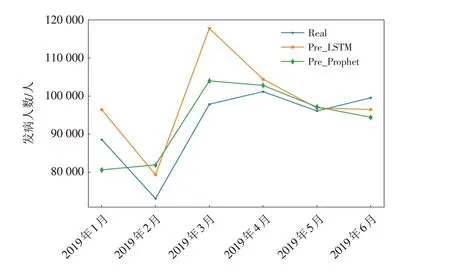
图7 LSTM模型与Prophet模型对比效果Fig.7 Comparison of LSTM model and Prophet model

由图7中两个模型6个月的预测曲线可以看出，两种模型均能较好地预测肺结核发病数的变化趋势；相比LSTM模型，Prophet模型预测曲线与肺结核发病数实际曲线更加接近，预测效果更好，能够更好地对发病数的趋势、发病数的周期进行拟合，并且，Prophet模型在发病数波动较大时也能有较好的拟合效果.

ARIMA模型与灰度模型常用于对传染病发病人数进行预测［6-7］，为进一步判断LSTM模型与Prophet模型的预测性能，本节对ARIMA、GM（1，1）、LSTM、Prophet四种模型的预测性能进行对比，运用四种模型对表1中2007年7月至2018年12月的数据进行训练，对2019年1月至2019年6月的数据进行预测，并计算各个模型的MAE与RMSE值，模型对比结果如表2所示.

表2 四种模型对比结果Tab.2 Comparison of four models

从表2可以看出，Prophet模型的MAE值与RMSE值分别为5 124.33、5 905.32，两项指标的值均低于其余三种模型，说明Prophet模型的预测性能最好. 通过比较ARIMA、GM（1，1）、LSTM、Prophet四种模型的MAE、RMSE值可以看出，ARIMA模型的预测性能在四种模型中表现最差，GM（1，1）模型略微优于ARIMA模型，而LSTM模型又优于GM（1，1）模型，其MAE值与RMSE值分别为6 851.71、9 287.70，仅次于Prophet模型.

4 结语

对肺结核发病数的准确预测能够为该病的防控工作提供一定的科学理论指导，本文将LSTM 模型与Prophet模型应用到肺结核月发病数的预测中. 实验结果表明，LSTM模型与Prophet模型均有较好的拟合效果以及预测性能. 并且，本文将以上两种模型的预测性能与ARIMA、GM（1，1）模型进行对比，对比结果表明Prophet模型的预测性能最好，其MAE值与RMSE值分别为5 124.33、5 905.32，其次为LSTM模型，ARIMA 模型预测性能最差.