基于改进灰色马尔可夫模型的实证分析——以上海入境旅客人数预测为例
2020-04-01郑芷雪
郑芷雪,郑 列
(湖北工业大学理学院,湖北 武汉 430068)
灰色GM(1,1)模型的亮点为样本数据少、原理易理解、计算简便、短时期预估准确率高、测试较容易。用修改初始值方法改进GM(1,1)模型,可以使模型拟合以及预测准确度有很大改善[1-2]。然而,由于灰色预测基于GM(1,1)模型对波动较大数据列拟合效果偏差大且预测准确度低。但是马尔可夫概率矩阵基于状态间的转移概率来预测将来发展,所以能预测波动大的数据列。将两个模型组合成改进的灰色马尔可夫预测模型,能有效使用数据,使得随机波动大的数据列预测准确度提高[3]。研究上海入境旅游历史数据,并预测上海入境旅游未来发展,可帮助我们从另一个角度和另一个层面了解上海的入境旅游市场,为上海旅游部门和旅游企业提供参考。
1 数据来源及说明
由于需求数据量少,本文将选取2010-2017年上海入境旅客人数为基础进行预测。为便于计算,将入境旅客人数的单位设成百万人次(数据来源于上海旅游局)。
2 研究方法
2.1 GM(1,1)模型
2.1.1 传统的GM(1,1)模型设非负原始序列为
X(0)={x(0)(1),x(0)(2),…,x(0)(n)}
对其进行一次累加生成,得其1-AGO序列为
X(1)={x(1)(1),x(1)(2),…,x(1)(n)}
(1)
解方程可得
以x(1)(1)=x(0)(1)为初始条件可得到灰色GM(1,1)模型的时间响应函数
(2)
离散化时间响应函数以获得灰色GM(1,1)模型的时间响应函数式
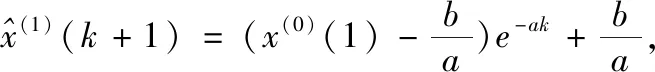
(3)
最小二乘原理估计灰色微分方程参数
(4)
其中,
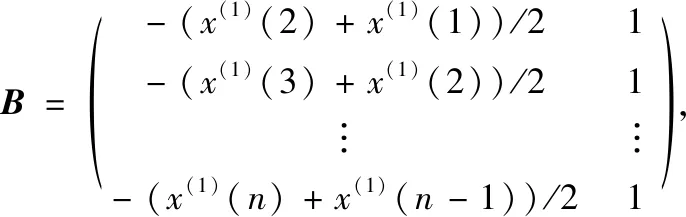
(5)
原始数据列预测值经一次累减还原得
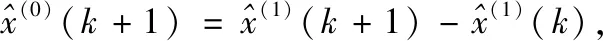
(6)
2.1.2 初值修正的GM(1,1)模型传统GM(1,1)模型以x(1)(1)=x(0)(1)为初始条件时,丢失了新数据带来的信息,因此采用将初始条件和新累加生成最后一项预测,以提高预测精度。建立模型,分别令t=1,n,可得:
(7)
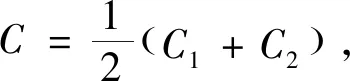
(8)
2.2 加权马尔可夫模型
加权马尔可夫链的基本原理是用一阶自相关系数来运算与用原始数据的状态参数值来预测。用时间相关强度加权求和,使预测结果更科学合理。加权马尔可夫模型[4]预测步骤如下:
1)利用均值均方差法等对原序列划分;
2)用1)中的方法划分状态区间;
3)检验原始随机序列的“马氏性”;
4)计算自相关系数
(9)
5)算出马尔可夫链非同步长的权重
(10)
6)算出每阶转移概率和相关转移概率矩阵;
7)限时段被认为是初始状态,转移概率矩阵是根据6)获得的,并且可预测对应于下一个时间段的概率,即
Pi(k),i∈E(k=1,2,…,m)
(11)
8)通过加权每个预测的概率,可获得如下状态的未来概率:
(12)
重复进行1)—7),可对下一时段的概率进行预测。
2.3 改进灰色马尔可夫模型
将初值修正GM(1,1)模型和加权马尔可夫模型结合成改进灰色马尔可夫模型。两个模型组合为
(13)
3 模型应用
由于灰色模型预估值发展趋向很单一,因此无法预估数据列波动特征,而马尔可夫模型能预测数据列的发展趋向。因此,联合两个模型的亮点,执行灰色模型初始值校正和马尔可夫模型加权,引入改进灰色马尔可夫模型来预测上海入境旅客人数。
3.1 初值修正的GM(1,1)建模
3.1.1 级比检验2010-2017年上海入境旅客人数建立初始序列[5]
{x(0)}=
{8.5112,8.1757,8.004,7.574,
7.913,8.0016,8.5437,8.7301}
(14)
通过计算得到该序列的级比
σ(k)=x(0)(k-1)/x(0)(k)=
{1.041,1.021,1.057,0.957,0.989,0.937,0.979}
(15)
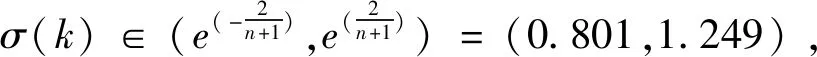
3.1.2 初值修正的GM(1,1)模型应用使用R软件运用传统GM(1,1)模型和初值校正GM(1,1)模型来预测2013-2017年上海入境旅客人数(表1)。根据表1,平均相对误差非常小,后验差在0.35~0.5之间,精度达到96%,在相对误差、后验差比值和精度三方面中看出,初值校正GM(1,1)模型比传统GM(1,1)模型预测结果好。故本文使用初值修正的GM(1,1)模型。
根据初值修正的GM(1,1)模型,可以得到参数估计值:
发展系数-a=0.0143;
灰色作用量b=7.6123。因此,灰色模型预测公式为
(16)
3.2 改进灰色马尔可夫模型应用
3.2.1 状态划分本文数据被分为5个状态区间,并使用初值校正GM(1,1)模型计算原始数列相应预测值。找出相应的残差序列和相对误差,并根据相对误差确定5个状态区间,取区间测度为1.2%。
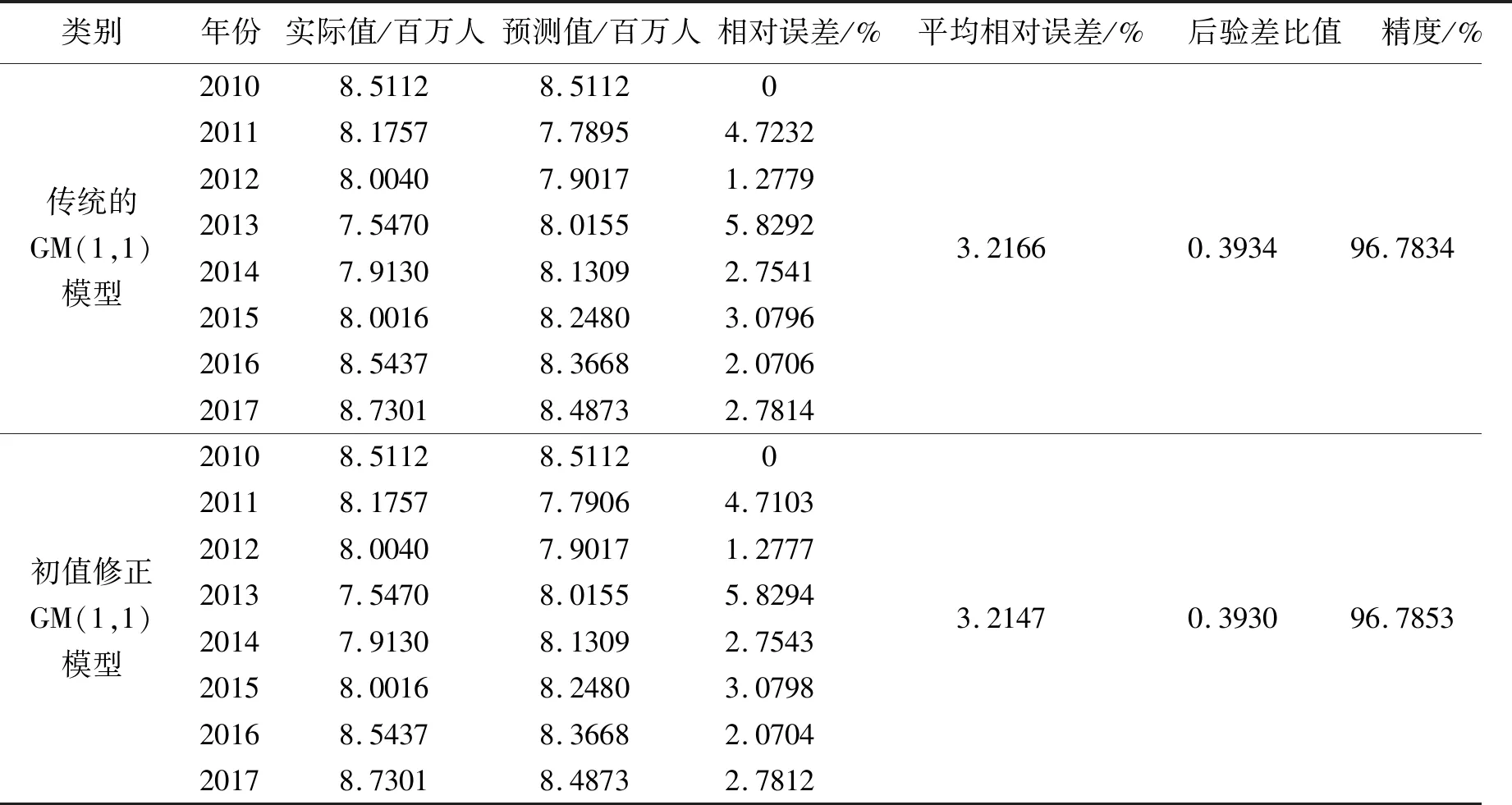
表1 上海入境旅客人数灰色模型预测值
状态区间E1=[0,1.2%),E2=[1.2%,2.4%),E3=[2.4%,3.6%],E4=[3.6%,4.8%],E5=[4.8%,6%]。这5个状态区间称为相对误差状态区间,基于初始数据和相对误差区间来确定初始数据所在的状态具体划分见表2。
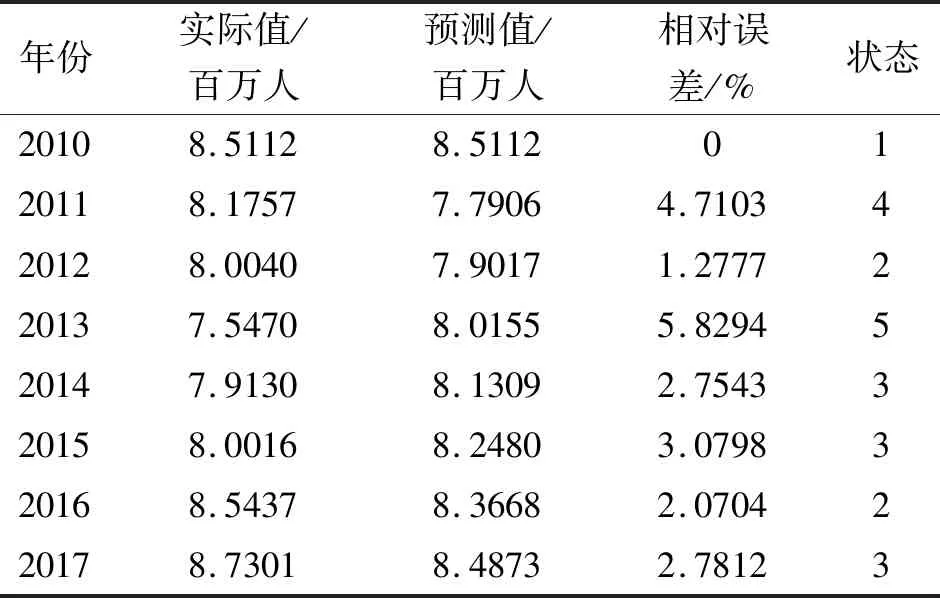
表2 根据相对误差划分状态
3.2.2 马氏检验使用MATLAB软件,转移频数矩阵
概率转移矩阵
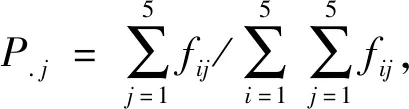
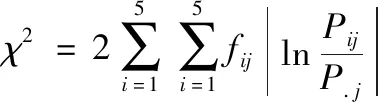
表3 统计量计算表
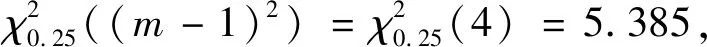
3.2.3 改进灰色马尔可夫模型应用分别算出步长为2,3,4,5对应的转移概率矩阵:
算出每阶自相关系数与每个步长的马尔可夫权重(表4)。
根据相对误差状态区间,结合加权思想,权重由状态边界值确定,因此,三个状态下对应的预测结果不同,结果表示成M(K+1),使用此模型预测上海入境旅客人数,具体形式运算如下。

表4 每阶自相关系数与每个步长的马尔可夫权重
状态1
状态2
状态3
(17)
状态4
状态5
在预测之前,有必要确定与目标年份数据相对应的状态,并预测下一年中相应值的状态,该状态由状态转移概率确定[7](表5)。
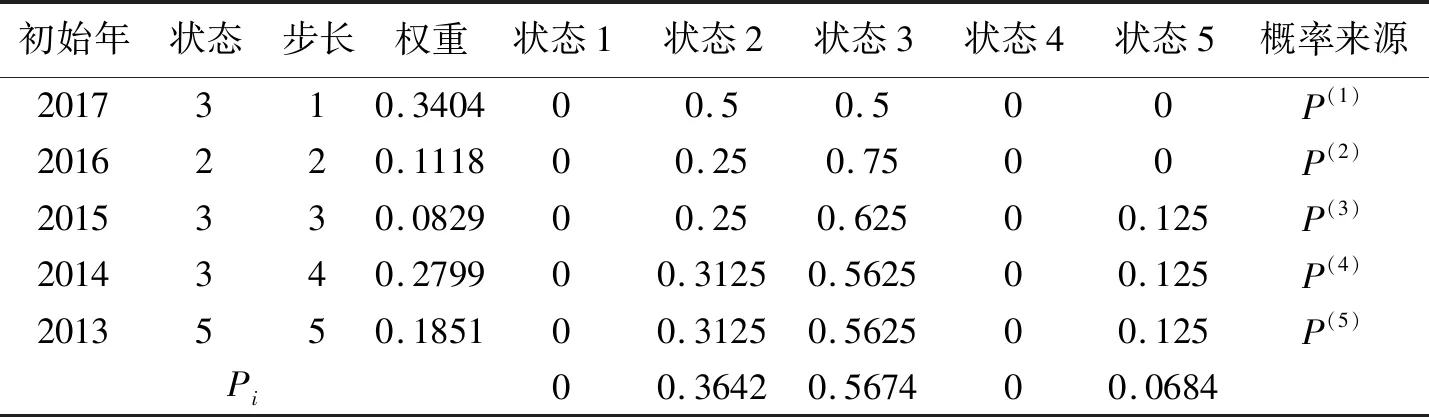
表5 2018年上海入境旅客人数概率预测表
从表5知,max{pi}=0.5674,2018年上海入境旅客人数的最大概率在状态3,即k=8时,用改进马尔可夫预测模型,2018年上海入境旅客人数为:
(18)
可以基于预测的2018年预测值的状态来计算2019年的状态,以此类推。根据上述计算步骤,2018-2020年上海入境旅游的人数可以依次预测,但预测的目标年份不能太大,由于政策等无法解释的因素可能会对灰色预测范围之外的数据产生影响,因此预测不准确。
使用改进灰色马尔可夫模型预测出2018-2020年上海入境旅客人数与相对误差,并使用改进GM(1,1)模型,预测2018-2020年上海入境旅客人数和相对误差,然后比较两者结果。
改进灰色马尔可夫相比改进GM(1,1)模型预测的相对误差小,前者平均相对误差是0.3048%,而后者平均相对误差为2.8129%。将2018年预测值与真实值比较,发现改进灰色马尔可夫模型预测值更加靠近真实值。因此,改进灰色马尔可夫模型在预测上海入境旅客人数方面结果更为准确。
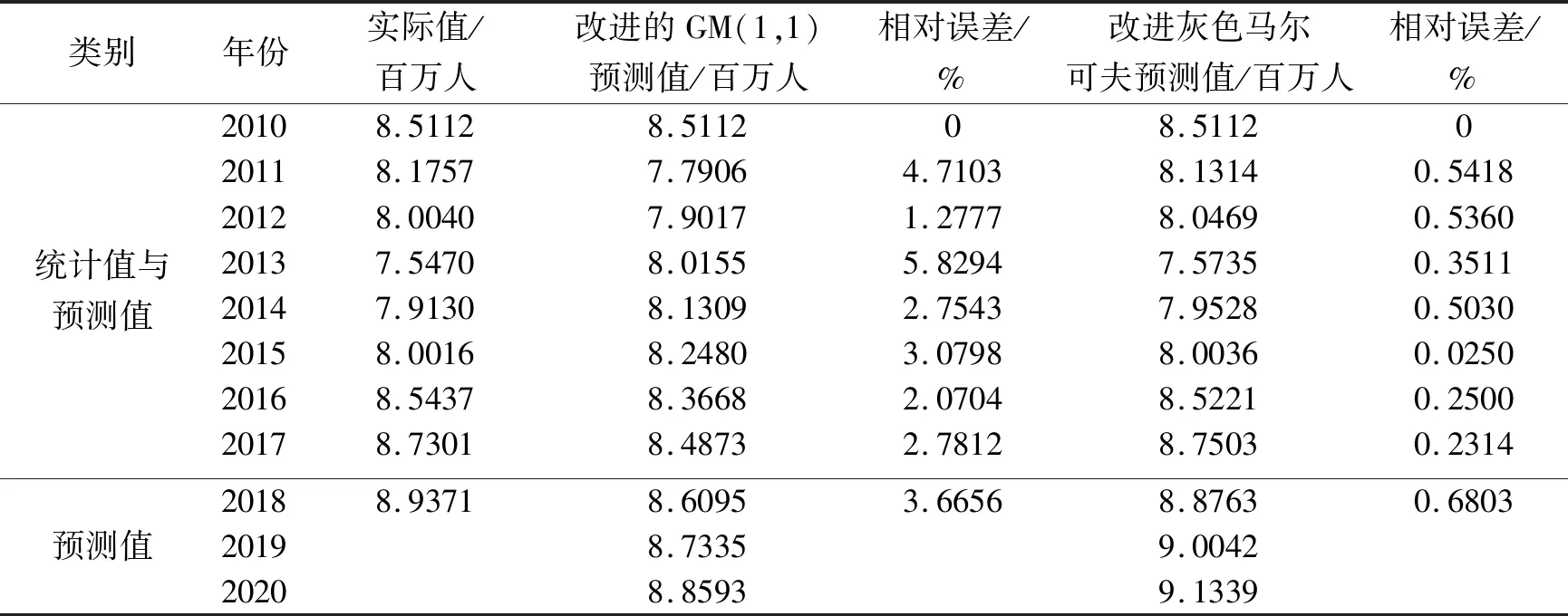
表6 上海入境旅客人数的改进灰色马尔可夫预测表
4 结论
1)上海入境旅客人数满足级比检验,可用传统GM(1,1)模型与改进GM(1,1)模型分别预测数据。在相对误差、后验差比值与精度三方面,可见初始值校正GM(1,1)模型比传统GM(1,1)模型预测结果更好。因此,可采用初始值校正的GM(1,1)模型。
2)通过测试获得的数据列具有马尔可夫属性,因为马尔可夫模型预测结果仅是一个区间而不是特定值。故将初值校正GM(1,1)模型和加权马尔可夫模型一起组合用于预测。组合模型比初值校正GM(1,1)模型预测结果的相对误差小,结果更精确。
