中国消费者价格指数应用研究——基于调和分整自回归移动平均模型
2020-04-01王锦,商豪
王 锦,商 豪
(湖北工业大学理学院,湖北 武汉 430068)
近年来用于刻画时间序列长记忆性特征的模型层出不穷,其中,Granger[1]和Hosking[2]提出的ARFIMA模型成为描绘时间序列长期记忆性常用的工具。ARFIMA模型克服了传统时序模型只能描绘短期记忆性的缺陷,通过引入分数维差分参数,使其具备拟合时间序列过程长记忆性的能力。ARFIMA模型得到广泛应用,但有学者指出该模型在拟合长期记忆性较弱的时间序列过程中是失效的[3-4]。基于此问题,Meerschaert[5]等人发现调和分整过程展现出的半长期记忆性(semi-long range dependence)能够很好地刻画长期记忆性较弱的时间序列过程。这种半长期记忆性具体表现为序列过程的自相关函数在前期缓慢下降,呈现双曲线形式,后期则以指数率迅速衰减。由此Meerschaert[6]在研究大气湍流速度数据的过程中首次在ARFIMA模型的基础上加入调和参数,提出了调和分整自回归移动平均模型(ARTFIMA),用以拟合具有半长期记忆性的平稳时间序列过程。
本文通过分析中国居民消费者价格指数的记忆特征,针对过程中存在的长期记忆性特征建立ARTFIMA模型,并与ARFIMA模型进行对比,最后通过谱密度拟合函数和预测效果验证ARTFIMA模型在中国居民消费者价格指数的拟合和预测方面比ARFIMA模型更具优越性。
1 模型说明
1.1 分整自回归移动平均模型
分整自回归移动平均模型ARFIMA(p,d,q)可以定义为整数阶差分ARIMA(p,D,q)模型的推广形式,其差分参数拓展到分数维[7]。ARFIMA(p,d,q)表达形式如下:
式中:d∈R且d<0.5,p,q∈Z;Φ(B)=1-φ1B-φ2B2,…,φpBp,Θ(B)=1+θ1B+θ2B2+…+θqBq分别为p阶自回归多项式与q阶移动平均多项式,Φ(B)=0,Θ(B)=0的所有根都在单位圆外,且没有重根;B为滞后算子;(1-B)d为分数维差分算子,即
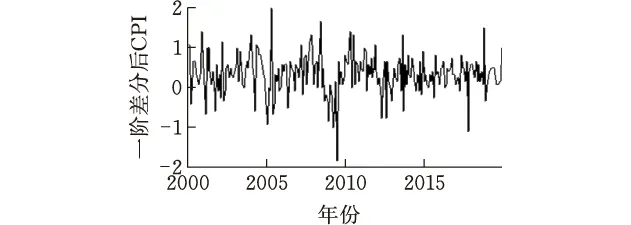
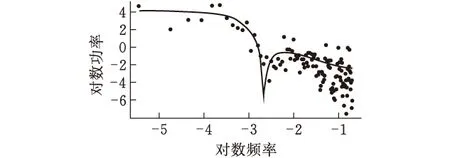
则称yt=xt-μt为分整自回归移动平均模型。当d<0.5,零均值的ARFIMA(p,d,q)过程是协方差平稳的;如果0 调和分整自回归移动平均模型ARTFIMA(p,d,λ,q)在上述ARFIMA(p,d,q)模型的基础上加入了调和参数λ。具体表达式如下: 式中:d∈R,λ>0,p,q∈Z;Φ(B)=1-φ1B-φ2B2,…,φpBp,Θ(B)=1+θ1B+θ2B2+…+θqBq分别为p阶自回归滞后算子与q阶移动平均滞后算子,Φ(B)=0,Θ(B)=0的所有特征根都在单位圆内,且没有公因子;B为后移算子;(1-e-λB)d是加入调和参数的分数维差分算子,即 (1-e-λB)df(t)= 本文的实证分析对象为中国居民消费者价格指数(CPI),数据来源于中国统计年鉴。选取从2000年2月到2019年3月共230个月度数据,数据无缺失和异常情况。初步的描述性统计分析结果显示样本数据呈现轻微右偏和尖峰分布。运用Jarque-Bera统计量检验得出CPI序列不满足正态分布。 表1 CPI序列的基本统计特征 从CPI序列的时间序列图(图1)可以看出,CPI序列没有明显的趋势性,但不具备平稳性特征。利用ADF方法检验CPI序列的单位根情况,结果显示序列非平稳。故对CPI进行一阶差分后得到一组新的时间序列,记为CPID1。一阶差分后的CPI序列的时序图如图2所示。CPI和CPID1的ADF检验结果见表2,从检验结果可以看出CPID1为平稳的时间序列过程,具备经典时间序列模型平稳性建模的前提条件。 图1 CPI原始数据时间序列图 图2 一阶差分后CPID1时间序列图 表2CPI和CPID1样本序列的单位根检验结果 D-F统计量值P值结果CPI-2.5520.107接受原假设,存在单位根CPID1-9.117<0.01拒绝原假设,不存在单位根 Hurst提出的重标极差分析法(R/S方法)是分析时间序列是否具有长期记忆性的有力工具,此方法通过计算Hurst指数判断时间序列数据存在的记忆特征。当Hurst指数介于数值0.5与1之间时,说明该序列存在持续性状态,即具有长期记忆性,且当Hurst指数越接近1,相关性越强,持续性状态越明显;Hurst指数越接近0.5,说明存在越大的噪声,持续性状态越微弱。Hurst指数H的计算原理如下[9]: 1)定义待研究的时间序列数据为{xt,t>0},将其划分为长度为n的A个连续子序列区间,每一个子序列区间记为Ia,a=1,…,A; 2)对各个子序列区间计算其均值 3)对每个子序列区间计算累积均值离差 4)计算每个子序列区间的标准差 5)计算A个子序列区间的平均重标度极差 其中Ra=max(yk,a)-min(yk,a),k=1,…,n是单个子序列区间的极差; 6)利用Hurst提出的模型,建立关系式 (R/S)n=(c×n)H 两边取对数可得 log(R/S)n=H×logn+logc 通过最小二乘回归求解H值。 利用上述R/S方法计算CPI序列的H指数,结果见表3。 表3 R/S长记忆性检验结果 根据R/S长记忆检验方法计算步骤,通过线性回归计算得出H=0.621,结合拟合优度R2统计量可知线性拟合效果较好。从H指数的数值来看,中国消费者价格指数序列存在长记忆性,但长记忆性较弱。 根据长记忆性检验结果,建立可以拟合时间序列长记忆性的ARTFIMA模型。首先针对一阶差分后的CPID1样本序列建立ARIMA模型,用以消除原始序列中存在的短期相关性。结合最小AIC和BIC准则(表4)选取p=2,q=2作为相对最优阶数。运用R软件和极大似然估计法[8]对CPI序列建立ARTFIMA(2,d,λ,2)模型并进行参数估计,参数估计结果见表4。ARTFIMA(2,d,λ,2)模型的参数估计结果见表5。 表4 ARIMA模型信息准则表(CPID1) 表5 ARTFIMA模型参数估计结果 模型表达式为: 结合前人的研究[10]和上述长记忆性检验的结果,建立长记忆ARFIMA(2,d,2)模型。利用极大似然估计法得出参数估计结果(表6)。 表6 ARFIMA模型参数估计结果 模型表达式如下: 3.4.1 谱密度拟合函数对比运用R软件画出上述建立的ARFIMA模型(图3)与ARTFIMA模型(图4)的谱密度函数拟合图,该图采用对数刻度反映频率与谱密度之间的幂律关系,其中黑色实心曲线为模型的光谱拟合情况。从谱密度函数拟合图的对比中可以看出,ARTFIMA模型在调和参数的作用下,对中低频处的数据进行了更好的拟合。 图3 ARFIMA模型谱密度函数拟合图 图4 ARTFIMA模型谱密度函数拟合图 3.4.2 预测效果对比运用上述建立的ARFIMA和ARTFIMA模型对中国居民消费者价格指数进行3期预测,结果如表7所示。 表7 预测效果对比 从预测结果可以看出,ARTFIMA模型预测误差为28.57%,而ARFIMA模型的预测误差达到37.34%,说明ARTFIMA模型在中国居民消费者价格指数序列的预测方面比ARFIMA模型更具优越性。 对上述两个模型产生的残差进行白噪声检验,用于验证建立模型的有效性。具体方法为:分别对残差序列和残差平方序列进行Ljung-Box纯随机性检验,仅当残差和残差平方序列同时通过Ljung-Box检验,才认为此残差是白噪声序列。从检验结果可以看出,各残差序列均是白噪声序列,说明模型拟合是合理的。 表8 残差白噪声检验 通过上述实证分析发现,中国居民消费者价格指数虽具有长期记忆性特征,但序列的相关性较弱,说明中国的消费者市场没有表现出随机游走的特性,并不是一个完全独立的过程,具有非线性、依赖性和潜在的可预测性。针对该序列表现出的长期记忆性建立ARTFIMA模型,取得了较好的拟合和预测效果,为针对时间序列过程记忆性的建模方法提供了新的视角和可能。1.2 调和分整自回归移动平均模型
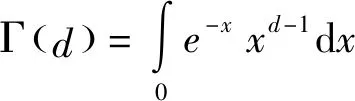
2 数据说明及预处理



3 实证分析
3.1 CPI序列的长记忆性检验

3.2 建立ARTFIMA模型


3.3 建立ARFIMA模型

3.4 模型对比


3.5 模型有效性检验

4 结束语
