基于神经过程-粒子群算法的移动机器人路径规划
2020-04-01王淑青毛月祥
马 烨,王淑青,毛月祥
(1 湖北工业大学电气与电子工程学院,湖北 武汉 430068;2 国网湖北省电力有限公司直流运检公司,湖北 武汉 430050)
移动机器人路径规划问题一直是机器人导航领域的研究热点。移动机器人路径规划是指机器人根据起点和终点坐标信息,搜索出一条能耗低、用时少、距离短,并且能避开所有障碍物的有效路径。PSO是模拟鸟类捕食的一种智能随机搜索算法[1]。相对于蚁群算法、遗传算法等,标准PSO算法具有易于实现、参数较少等优点,但是基本PSO算法存在早熟和局部收敛,后期算法多样性降低,算法精度得不到提升等问题,为此国内外相关作者做了大量研究,并提出了各种改进算法。赵甜甜引入细菌觅食优化算法和PSO算法结合,缩短了搜索时间,减少了迭代次数[2]。贾会群等引入鸡群算法的母鸡更新方程和小鸡更新方程对搜索停滞的粒子进行扰动,使粒子向全局最优解靠近[3]。蒲兴成等将反向策略引入PSO算法,提高了粒子群算法的寻优能力和稳定性[4]。综上所述,制定有效的机制使粒子逃离局部最小值并提高收敛精度是提高粒子群算法性能的关键。本文提出了神经过程-粒子群混合算法的移动机器人路径规划。首先建立环境模型,在传统粒子群算法的基础上,引入神经过程预测每一代粒子的个体位置,在保证粒子多样性的同时,增加了粒子摆脱局部最优的能力。最后对基于神经过程-粒子群混合算法和传统粒子群算法进行了仿真实验,仿真结果验证了本文算法在路径规划应用上的优越性和可行性。
1 路径规划
1.1 路径规划问题描述
由于启发式智能技术可以有效地解决约束优化问题,所以把路径规划问题转化为约束优化问题是目前常用的一种方式[5]。通过建立路径长度、平滑度、碰撞距离等约束函数,将寻找最优路径转化为寻找函数最优值,从而实现移动机器人的路径规划。
1.2 环境建模
目前基本的环境建模方法主要有栅格法、可视图法和拓扑法等[6]。其中可视图法通过映射环境信息为几何形状,可以简化路径规划为寻找最短路线的约束优化问题,因此本文采取可视图法进行环境建模。图1为移动机器人路径规划的环境模型。在该模型中,障碍物以不同形状和大小的实体的形式呈现,通过建立起点S到终点T的局部坐标系S-X′Y′,由D条垂直于X′的直线L1~LD将路径平均分成D+1段,在垂直线Li(i=1,2,…,D)上随机选取一个没有碰撞的节点Pi,构成一条完整的路径
Ppatp={P1-S,…,PD-PD-1,T-PD}
要得到全局坐标系O-X′Y′中路径上的任意点,需要得到局部坐标系与全局坐标系之间的变换矩阵。x′(d),y′(d)在局部坐标系上可以转化为在全局坐标系统的x(d),y(d),转换方程如下
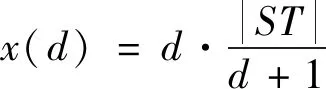
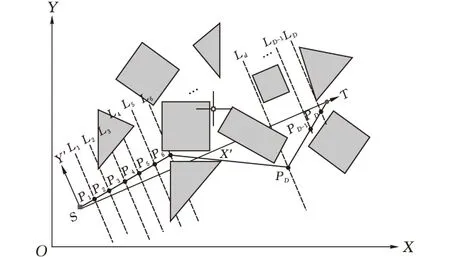
图1 移动机器人路径规划的环境模型
1.3 建立适应度函数
适应度函数用于评价移动机器人路径规划的性能,其中主要有三个性能指标:路径长度、安全性和路径平滑性。在本文中,路径长度和平滑度相结合,用于评价移动机器人的路径规划性能标准。适应度函数如下
F(P)=ω1·L(P)+ω2·S(P)
其中‖Pi+1-Pi‖表示Pi到Pi+1的欧氏距离。αi表示路径生成的第i个偏转角(弧度范围为0到π),(Pi-Pi-1)·(Pi+1-Pi)表示(Pi-Pi-1)和(Pi+1-Pi)向量之间的内积,|Pi-Pi-1|和|Pi+1-Pi|表示向量范数。ω1和ω2分别对应路径长度和平滑度的权重系数。
2 神经过程-粒子群算法的移动机器人路径规划
2.1 神经过程
神经过程(NPs)是一个基于神经网络的公式,它学习了一个随机过程的近似,是一类结合了神经网络和随机过程优点的模型[7]。NPs显示了高斯过程的一些基本特性,即对函数分布进行建模,能够根据观察样本点来估计预测的不确定性,并将一些工作负载从训练转移到测试时间,给予了模型的灵活性,而且NPs可以以更高的效率生成预测。在给定n个样本点和m个目标点的情况下,经过训练的神经过程推理对应于深度神经网络中的正向传递,深度神经网络的尺度为o(n+m),远少于经典高斯过程中的o(n+m)3。

(a)神经过程的图形模型

(b)神经过程执行图图2
图2a中x和y对应于函数y=f(x)的数据。C和T分别为样本点和目标点的个数,z为全局潜在变量。灰色背景表示观察到该变量。图2b中圆圈的变量对应于图2a中的图形模型中的变量,方框中的变量对应于NPs的中间表示形式,粗体字母对应于以下计算模块:h-编码器、a-聚集器和g-解码器。在实现过程中,h和g对应于神经网络,a对应于均值函数。连续线描述生成过程,虚线描述推理过程。
在执行神经过程期间必须考虑两个条件:样本点顺序的不变性和计算效率。得到的模型可以归结为以下三个模块(图1b):
1)从输入空间到表示空间的编码器模块h,h被参数化为一个神经网络,它接受一对(x,y)的样本点,ri=h((x,y)i)为编码器h对每一对样本点产生的一个对应的输出。
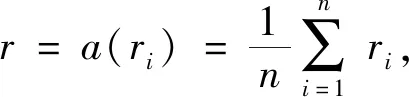
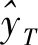
2.2 粒子群算法
粒子群优化算法(PSO)最基本的算法模型就是带惯性权重的PSO模型[8]。其模型描述为

其中c1和c2为学习因子;r1和r2为[0,1]区间内的随机数;v和x分别为粒子速度和位置,t为代数,i为粒子编号,d为空间维数,p(p-best)i和pg-best分别为个体和群体的最优点;ω是惯性因子。
2.3 神经过程-粒子群算法
粒子群的运动过程是一个随机过程,而神经过程是学习一个随机过程的近似,将每一次迭代过程中各个粒子的位置和神经过程输出的粒子预测位置保存为样本点,粒子的位置和预测位置与当前全局最优点差值最小的点作为目标点,这样在迭代过程中不断进行,粒子可以快速找到当前全局最优点,并且粒子也不会丧失其多样性,在神经过程的不断预测中,跳出局部最优。神经过程-粒子群算法可以保证粒子的多样性,显著减少预测过程的计算量,提高算法速度的同时避免算法陷入局部最优。算法描述为
xi+1=f(xi),C={xi,x2,…,xT-1}
yT=g(xT)
其中:函数f(x)为粒子群的运动过程;gx为参数化的神经网络即神经过程;xi为第i次迭代时的粒子位置;C为目标点集,包含了第1次迭代至第T-1次迭代时粒子位置的集合;xT为当前迭代次数T时的目标位置;yT为得到的预测位置。
2.4 实现流程
神经过程-粒子群算法的移动机器人路径规划的流程见图3。
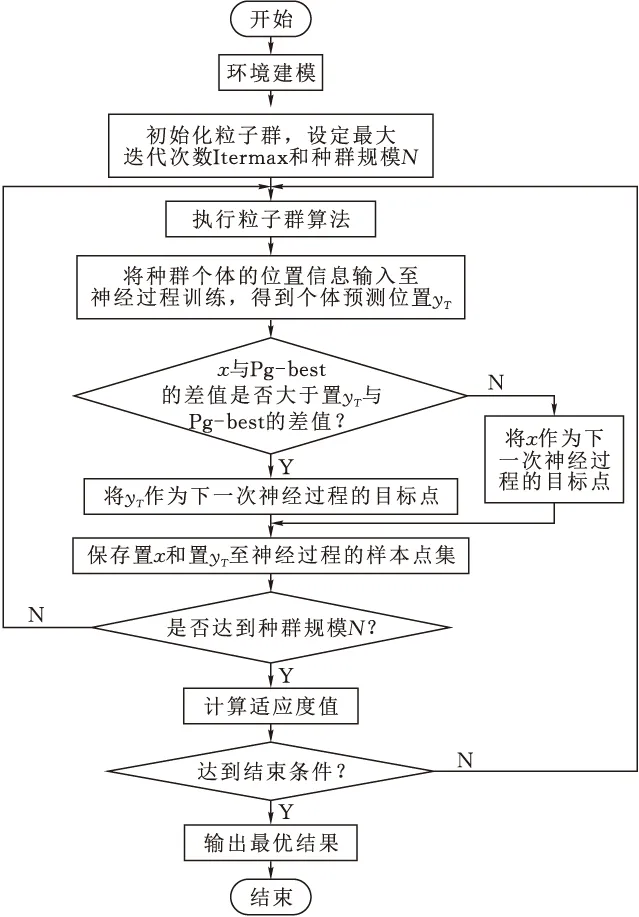
图3 神经过程-粒子群算法的移动机器人路径规划
3 仿真实验与分析
本文选取常见的Rastrigin函数验证算法的全局寻优能力。Rastringin函数有非常多的局部极小点,而仅仅只有一个全局最小点,这个点就是(0,0),在该点处的函数值为0,因此该函数被用来评价算法的优化性能。图4为函数的运行结果,本文算法在迭代42次时达到最优解,而传统PSO算法在迭代38次陷入局部最小值,经过200次迭代仍然不能达到全局最小值。
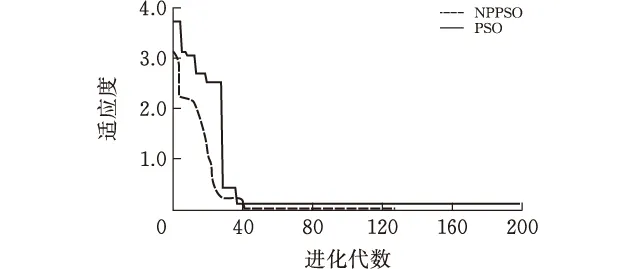
图4 Rastrigin函数运行图
随机生成一组具有多个障碍物的700×700地图进行仿真实验。仿真参数如下:粒子的个数为N=100,维度D=10,加速因子c1=c2=1.4962,最大迭代次数MaxDT=200。
由图5与图7所示的传统PSO算法和图6与图8所示的本文神经过程-粒子群算法可知,两种算法都能从起始点避开障碍物到达终点,但是传统PSO算法规划出的路径经过了较多的障碍物边缘,并且选择的不是最优并且最短的路径。本文提出的NPPSO算法从平滑度和长度而言,均优于传统PSO算法规划出的路径,有效地避免了与障碍物边缘相切的非最优路径。

图5 传统粒子群算法路径规划仿真
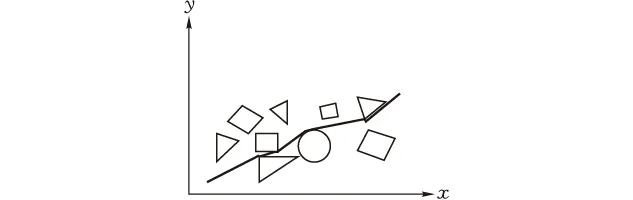
图6 本文算法路径规划仿真
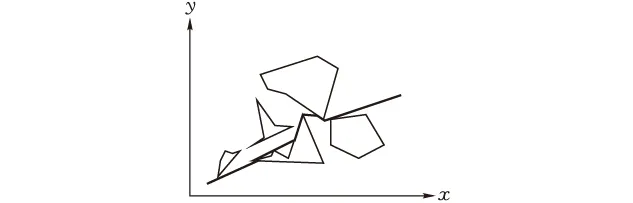
图7 传统粒子群算法路径规划仿真

图8 本文算法路径规划仿真
4 结束语
本文提出了一种基于神经过程-粒子群算法的移动机器人的路径规划,通过在粒子群的迭代过程中引入预测运动的神经过程思想,保证了粒子的多样性,避免陷入局部最优。采用Rastrigin函数对本文算法进行性能评估,取得了良好的测试结果,并且在随机建立的环境模型下,能够有效、准确地得到目标点的路径。
