基于改进磷虾群算法优化ESN的短期负荷预测

陈馨凝，刘 辉，刘雨薇，邹琪骁，李侯君

(湖北工业大学电气与电子工程学院，湖北 武汉 430068)

准确的负荷预测对于电力系统的发电计划以及经济运行尤为重要[1-2]。电力系统的短期负荷预测成为电力系统发电计划中的重要课题，国内外学者也对此进行了大量研究。文献[3]利用核主成分分析法对初始输入量进行数据处理，消除冗余信息对ELM神经网络模型的影响，同时提高了模型的预测准确度。文献[4]将改进遗传算法和BP神经网络结合提出了一种预测新方法，研究表明该方法具有一定的有效性，但仍无法完全避免BP神经网络局部寻优能力不足等缺陷。文献[5]提出了一种基于PSO-WPESN的电力负荷预测模型，仿真证明其模型稳定性和预测精度都明显提高，但由于算法嵌套，模型存在预测时间较长的缺点。为了更加有效且准确地预测短期电力负荷，本文结合改进磷虾群算法和回声状态神经网络，提出了一种新型电力负荷预测模型，该模型首先利用核主成分分析法对影响因素进行降维，选取主要成分作为网络的输入量，然后利用改进磷虾群算法对ESN隐含层到输出层之间连接权值进行优化，从而达到提高模型预测精度的目的。

1 磷虾群算法

1.1 标准磷虾群算法

磷虾群算法(Krill herd，KH)是由美国学者GANDOMI等人根据南极海洋磷虾觅食过程提出的一种新型仿生学算法[6]，该算法是以磷虾群中各磷虾个体之间的相互作用为基础的群智能算法，通过迭代寻求磷虾的最优位置解。单个磷虾位置更新主要由以下三个运动控制[7-8]。

1)其他磷虾个体诱发的运动

2)磷虾本身的捕食运动

3)磷虾本身的随机扩散

(1)

其中，Dmax表示随机扩散速度极限值，Imax表示算法的最大迭代次数，δi表示随机移动的方向，取值为-1到1之间的任意数。

根据以上三种运动，磷虾的位置更新如下：

(2)

(3)

Δt是每个磷虾在运动中的寻优步长，且

(4)

其中，NV表示待求解问题的维数，Uj和Lj分别表示第j个磷虾的寻优边界，其差值的绝对值为磷虾的寻优范围，Cj表示搜索步长因子，其值为介于0到2之间的常数。

因此，每个磷虾个体的位置在上述三种移动的综合影响下，不停进行迭代并更新，直到符合算法结束条件时停止，当前位置对应的解即为算法的最优解。

1.2 磷虾群算法的改进

随着迭代次数达到一定数量，磷虾群的个体特征将会被削弱，从而容易陷入局部最优[9]。因此算法必须协调好两者之间的关系，才能使得算法性能更好地发挥。

1.2.1 引入扰动因子λ 为进一步优化磷虾群算法，将下式所示的变异因子加入随机扩散运动：

λμ·fitness

其中，μ表示变异系数，其值随着迭代次数的增加由1减小到0；fitness表示磷虾个体的适应度值，其值越小越好。

由于变异系数呈现递减趋势，加入扰动因子后的磷虾群算法具有以下优点：

1)在算法迭代初期，变异系数会产生较大范围的变异，此时算法将获得较优的全局遍历能力；

2)在算法迭代中期，由于变异系数逐渐减小使得周边搜索能力大大提高，此时算法将获得良好的局部搜索性能和快速性;

3)在算法迭代后期，由于存在较大适应度值的磷虾，此时算法将获得较大的寻优范围，以达到优化标准磷虾群算法，避免易陷入局部最优的目的。

1.2.2 精英选择和保留策略本文将精英选择和保留策略加入标准磷虾群算法的迭代中对其进行优化：首先计算每个个体初始位置所对应的适应度值，选取其中适应度值最优的个体作为群体中的精英虾，并记录为Fbest；在三种运动的共同影响下磷虾位置不断移动，每次更新计算当前磷虾的适应度值并与精英虾作比较，选择更优的磷虾并记录在Fbest中。直到算法停止时，记录的适应度值即为全局最优解。

改进后的磷虾群算法更全面多样地考虑了迭代过程和单个磷虾的具体状况，提高了算法的收敛速度，增加了算法的稳定性。

2 ESN神经网络

回声状态网络(Echo State Networks)由Jaeger于2001年提出的一种新型神经网络[10-11]，其结构特点是具有非线性神经元的高度互联和递归拓扑，构成了包含大量输入和输出模式历史的信息的储备池，大量内部神经元被反馈到无记忆但自适应的线性网络，产生网络输出。并且，ESN能够将RNN训练的复杂性降低到简单的线性回归，改善了RNN训练时间长的缺点，体现了回声状态网络的优越性。其网络结构见图1，ESN同样是由输入层、隐藏层、输出层组成。

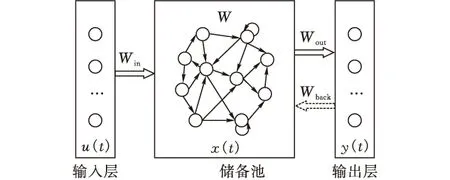
图1 ESN神经网络结构图

2.1 输入层(Input Layer)

2.2 储存池(Reservoir)

2.3 输出层(Readout)

存储池到输出层为线性连接关系，即输出方程满足：

ESN网络训练过程的实质就是训练Wout的过程，并且通过简单的线性回归即可完成。因此，相比其他神经网络，ESN能够快速准确地运行，且一定程度上避免了梯度下降的优化算法中出现的局部极小情况。

3 基于改进磷虾群算法的回声状态网络

为了更加精确地对电力负荷进行评估，首先采用KPCA对原始数据进行有效降维，然后运用改进磷虾群算法对回声状态网络的权值进行优化，构造出短期电力负荷模型[12-13]。基于IKH-ESN模型建立的具体步骤如下：

步骤一：初始化改进磷虾群算法各参数：设定其磷虾群的个体数为Np、算法最大迭代次数Mi、诱发个体的最大速度Nmax、个体的捕食速度Vf和最大扩散移动速度Dmax等。

步骤二：初始化ESN神经网络结构：输入层节点数量、动态储备池DR数量、输出层节点数量、谱半径γ、随机生成Win、W、Wback矩阵，确定目标函数。

步骤三：计算适应度值：根据下式计算各磷虾的适应度值，对比后选出适应度最小的磷虾个体为精英虾，并记录其位置信息为Fbest。

步骤四：综合磷虾个体的三种运动对磷虾个体位置的影响，根据式(2)～(4)对磷虾个体位置进行更新，并计算出当前位置下的适应度值与Fbest对比，选出更优磷虾位置所对应的适应度值存储在Fbest中。

步骤五：判断适应度值是否满足算法结束条件，若不满足则返回步骤三更新磷虾位置并继续重复迭代。

步骤六：若满足则算法结束，此时全局历史最优位置即为ESN神经网络的输出权值矩阵Wout，利用优化的网络参数进行训练及负荷预测。

基于改进磷虾群算法的回声状态网络流程见图2。

图2 IKH-ESN模型流程图

4 实例仿真

为证明本文所提出的新模型在电力负荷预测方面具有优越性，采用河南省某地区2018年6月的实际负荷数据进行建模和测试，该负荷数据采样间隔为15 min，即选取连续2880(96×30)组数据作为样本。由于短期负荷数据受历史负荷、温度、日属性等环境因素影响，因此选取预测点前6天同一时刻的历史负荷数据X1-X6，预测点前4个时刻的历史负荷数据X7-X10，以及预测点的日属性X11、预测点的温度X12共12个输入变量。

4.1 初始数据处理

由于初始输入变量较多，本文首先运用核主成分分析(KPCA)方法[14]对初始数据进行处理。得到的结果见表 1。由表1可知，经过核主成分分析，前 7个主成分的累加贡献值已超过95%，可以认为这7个核主成分可以很大程度上反映原本12个主成分的数据特征，因此选取前7个主成分作为IKH-ESN模型的输入量。

表1 核主成分分析结果

4.2 IKH-ESN模型预测

本文选取6月1日到6月30日的负荷数据进行预测，采用每隔15 min测试的方式选取共2880组数据，首先选取6月1日到6月29日的2784组样本数据作为训练样本，输入预测模型中反复进行训练。根据KPCA降维处理的结果，IKH-ESN模型采用输入层节点a=7，输出层节点b=1，储备池节点数DR=1000，谱半径γ=0.75，稀疏度SD=0.03，输入单元尺度IS=0.35的7-1000-1的网络结构。其中设定改进磷虾群算法的初始参数为：Np=30，Mi=100，Nmax=0.03 m/s，Vf=0.01 m/s，Dmax=0.005 m/s。当训练完成后，利用6月30日的96组负荷数据作为测试样本，最终得到的模型输出值与实际负荷值进行对比分析。

为了进一步体现本文构建IKH-ESN模型的优越性，同时构建了标准BP、标准ESN以及PSO-BP模型三种模型方法作为对比，其中标准BP模型采用7-5-1的网络结构输入层节点，迭代次数为100；标准ESN模型网络结构与本文相同；PSO-BP模型初始参数设定为：速度更新参数均为1.5，迭代次数为100，种群数量为20。

经仿真计算得到各模型的电力负荷预测曲线(图3)，大致上，各模型的预测效果都比较好。但是通过90-96点的放大图可以看出:IKH-ESN的预测值与实际值曲线相错相交，十分接近，预测效果最好；PSO-BP的预测值与实际值曲线大致相同但存在一定差距，预测效果其次；而BP和ESN预测值出现大波度的波动，预测准确度相对较低。

(a)各模型预测结果

(b)预测结果局部放大图图3 6月30日负荷预测曲线

各模型的预测误差百分比(图4)可以看出，BP模型误差在-8.87%～7.43%之间，ESN模型误差在-7.06%～6.08%之间，PSO-BP模型误差在-3.95%～5.54%之间，而IKH-ESN模型误差仅在-2.56%～2.38%之间。图4b显示的是误差百分比绝对值，可以清晰看到，IKH-ESN的误差百分比绝对值要远小于其他模型。图5为各模型的迭代次数，由图5可看出，经IKH算法的收敛速度最快，在第24代时就达到收敛。最终其适应度值为0.001667。说明通过改进磷虾群算法优化ESN能够有效克服传统ESN的缺陷，达到精准预测的目的。

(a)各模型预测误差

(b)各模型误差绝对值图4 各模型预测误差百分比

图5 各模型迭代次数

为了更加直观地比较IKH与其他智能算法的优化效果，本文从MSE、RMSE、MAD、迭代次数、收敛时间对上述4个模型的精度进行描述(表2)。由表2可以看出，IKH-ESN模型具有最佳预测精度，其RMSE、MAPE、ME分别为1.308，1.481、32.612，其预测精度和泛化能力相比其他算法得到明显提高，其误差精度较传统BP提高3.892%，较ESN神经网络提高了2.962%，较PSO-BP模型提高了1.807%。由于IKH算法叠加优化作用，模型预测耗时达到2675 s，但相比PSO-BP模型，收敛速度有所提高，同时避免传统神经网络以及回声状态神经网络易陷入局部最小的缺陷。综上所述，基于改进磷虾群算法优化回声状态网络模型的预测效果相比其他方法效果更优。

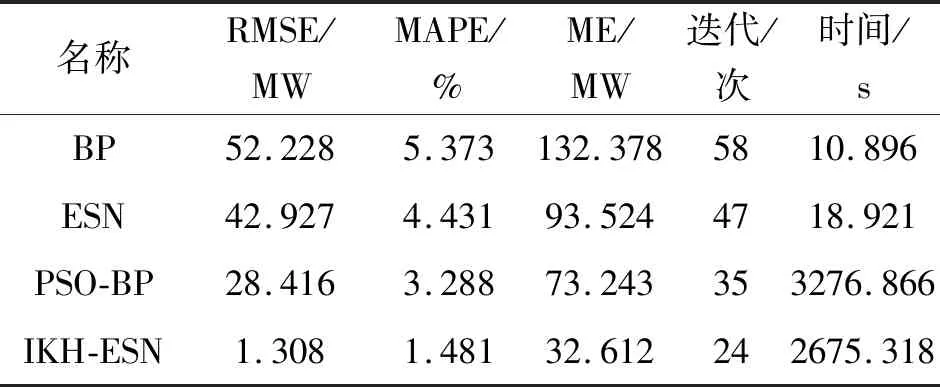
表2 各模型的预测效果

4 结论

本文提出了一种基于改进磷虾群算法优化ESN的短期负荷预测方法。考虑电气系统负荷的复杂性，将改进磷虾群算法和回声状态神经网络两者组合优化，首先采用核主成分分析法对初始输入量进行优选，再使用IKH-ESN模型对优选后的数据在MATLAB工具箱中进行预测。同时与传统BP、传统ESN以及PSO-BP三种预测模型进行对比，仿真结果表明本文所提出的新模型具有更高的预测精度和收敛速度。鉴于负荷的不确定性，未来可进一步考虑其他因素对负荷预测的影响，提高该模型的普遍适应度。