一种方法破解十三种变形

■河北省南宫市教育局教研室

■河北省南宫中学 霍忠林

赋值法是二项式定理的一个重要应用,它体现的是一种从一般到特殊的转化思想。用赋值法处理二项式展开式中与项的系数相关的问题,一直以来都是各地高考及模拟考试的热点问题。本文从一道例题出发,通过十三个由浅入深的变式,将赋值法常见的各种题型一一归纳总结,以期对同学们提供帮助。

例题若(3x-1)7=a0+a1x+a2x2+…+a7x7,求a0+a1+…+a7的值。

解析：令x=1,则a0+a1+…+a7=27。

变式1若(3x-1)7=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,求a0+a1+…+a7的值。

解析：令x=2,则a0+a1+…+a7=57。

变式2若(3x-1)7=a0+a1(2x-1)+a2(2x-1)2+…+a7(2x-1)7,求a0+a1+…+a7的值。

解析：令x=1,则a0+a1+…+a7=27。

评析：运用赋值法在解决形如“(ax+b)n=a0+a1(sx+t)+a2(sx+t)2+…+an(sx+t)n(a≠0,s≠0),求a0+a1+…+an的值”问题时,只需令sx+t=1,即将带入等式左边,从而得到所求结果

变式3求(3x-1)7的展开式中所有项的系数和。

解析：该变式与变式1相同,只是形式上没有变式1更“直观”,答案略。

变式4求(2x+1)(3x-1)7的展开式中所有项的系数和。

解析：令x=1,则展开式中所有项的系数和为3·27。

变式5求(2x+y)(3x-y)7的展开式中所有项的系数和。

解析：令x=y=1,则展开式中所有项的系数和为3·27。

评析：运用赋值法在解决形如“求(ax+by)n(cx+dy)m(其中a,b,c,d为常数)展开式中所有项的系数和”问题时,只需将两变量x=1,y=1代入等式左边,从而得到所求结果(a+b)n(c+d)m。

变式6若(3x-1)7=a0+a1x+a2x2+…+a7x7,求a0-a1+a2-a3+…+a6-a7的值。

解析：令x=-1,则a0-a1+a2-a3+…+a6-a7=(-4)7。

评析：运用赋值法在解决形如“(ax+b)n=a0+a1(sx+t)+a2(sx+t)2+…+an(sx+t)n(a≠0,s≠0),求a0-a1+a2-…+(-1)nan的值”问题时,只需令sx+t=-1,即将代入等式左边,从而得到所求结果

变式7若(3x-1)7=a0+a1x+a2x2+…+a7x7,求a1+a3+a5+a7和a0+a2+a4+a6的值。

解析：注意到a0+a1+…+a7=27,a0-a1+a2-a3+…+a6-a7=(-4)7。

变式8若(3x-1)7=a0+a1x+a2x2+…+a7x7,求|a0|+|a1|+…+|a7|的值。

解析：注意到a0,a2,a4,a6均为负数,a1,a3,a5,a7均为正数,所以：

|a0|+|a1|+…+|a7|

=-a0+a1-a2+a3-a4+a5-a6+a7

=-(a0-a1+a2-a3+a4-a5+a6-a7)=-(-4)7=47。

评析：对比(3x-1)7和(3x+1)7展开式中次数相同项的系数,易发现变式8中|a0|+|a1|+…+|a7|的值就等于(3x+1)7展开式中各项的系数之和,因此在运用赋值法解决形如“(ax+b)n=a0+a1x+a2x2+…+anxn,求|a0|+|a1|+…+|an|的值”的问题,就可以转变为“求（|a|x+|b|）n展开式中各项的系数之和”问题来处理。

变式9若x7=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,求a0+a1+…+a7的值。

解析：解法一,令x=2,则a0+a1+…+a7=27。

解法二,令t=x-1,则(t+1)7=a0+a1t+a2t2+…+a7t7。再令t=1,则a0+a1+…+a7=27。

评析：解法二通过换元将问题转化为同学们熟知的问题,这种处理尤其在求特定项的系数时(比如本题中若求a2的值),非常便利。

变式10若x7=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,求a1+2a2+3a3+…+7a7的值。

解析：x7=a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,两边分别对x求导得：

7x6=a1+2a2(x-1)+3a3(x-1)2+…+7a7(x-1)6。

令x=2,得a1+2a2+3a3+…+7a7=7·26。

评析：运用赋值法在解决形如“(ax+b)n=a0+a1(sx+t)+a2(sx+t)2+…+an(sx+t)n(a≠0,s≠0),求a1s+2a2s+3a3s+…+nans的值”问题时,可将等式两边分别先对x求导,再赋值来处理。当a=1,b=0,s=1,t=-1,n=7,就是变式10。特别地,有时候需要对等式两边多次求导,再赋值,比如变式11。

变式11若(3x-1)7=a0+a1x+a2x2+…+a7x7,求2a2+6a3+12a4+20a5+30a6+42a7的值。

解析：(3x-1)7=a0+a1x+a2x2+…+a7x7,两边分别对x求导得：

21(3x-1)6=a1+2a2x+3a3x2+4a4x3+5a5x4+6a6x5+7a7x6。

两边再对x求导得：

378(3x-1)5=2a2+6a3x+12a4x2+20a5x3+30a6x4+42a7x5。

令x=1,得2a2+6a3+12a4+20a5+30a6+42a7=378·25。

变式12若(3x-1)7=a0+a1x+a2x2+…+a7x7,求的值。

解析：令

评析：由于待求式子中各分母的次数与对应分子中下标的数字相同,因此可以直接进行赋值即可。

变式13若(3x-1)7=a0+a1x+a2x2+…+a7x7,求的值。

解析：两边各自在区间[0,t]上求积分,得

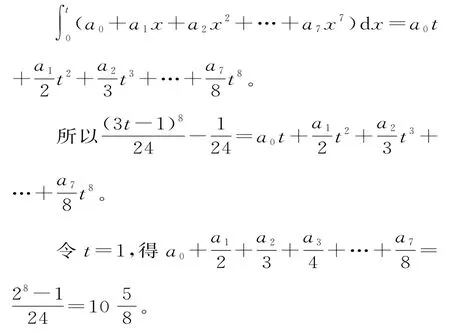
评析：注意本题与变式12的区别,本题中分母数字比对应的分子次数多1,容易想到公式因此可以借助于定积分来处理。

总之,运用赋值法处理二项式展开式中与系数和有关的问题时,要注意观察所求式子的结构特征,灵活“赋值”,才能顺利解决问题。这种解决问题的能力,需要同学们自己“琢磨—总结—内化—应用”,只有这样才能不断地提高大家的学科素养。