基于改进小波去噪的图像边缘检测算法

张 鹏

（安徽新闻出版职业技术学院 安徽合肥 230601）

1 引言

随着机器视觉领域图像采集技术的进步与革新，如何获得图像关键信息成为重点研究的问题。图像的基本特征信息一般存储在边缘轮廓中，提取图像边缘信息是数字图像处理、图像分析、特征识别的基本步骤，并且可以节约图像处理过程中数据存储量，为获取更深入的图像处理结果提供基础［1］。但是由于图像传感器设备自身因素、外界环境因素常常导致原始采集的图像布满各种类型的噪声，影响有效信号识别与检测，降低图像边缘检测精度［2］。为此，文章在检测图像边缘信息之前首先对图像进行小波去噪处理，以降低后期图像边缘检测的难度；然后采用梯度算法检测图像的边缘信息。希望通过该研究形成一套行之有效且节省计算量的图像边缘检测算法，为数字图像研究提供一种高效率与高精度的图像分析手段。

2 改进小波去噪算法在图像边缘检测中的应用

2.1 小波阈值去噪思想及阈值函数选取

图像去噪算法中小波阈值去噪原理应用广泛，去噪思路如下：首先图像噪声的高频区域实施阈值处理，然后重构阈值处理后的小波系数，获得去噪后的高清晰度图像。所以，基于小波阈值法进行图像去噪要重视阈值及阈值函数的选取，这两个参数关系到图像去噪的最终效果。经过广泛的图像去噪实践应用可知，当小波阈值取值较小时图像噪声去除不彻底、干扰边缘检测效果；当小波阈值取值较大时图像特征去除过度，造成图像失真模糊［3］。解决小波阈值去噪问题期间，采用公式描述图像中高斯白噪声的数学形式：

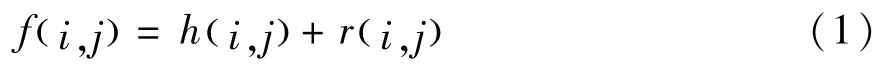
式（1）中，图像像素点的位置信息采用i，j描述；高斯白噪声为r(i，j)，服从正态分布N(0，δ2)；那么带有高斯白噪声的图像以及不带噪声的图像分别采用f(i，j)、h，(i，j)表示。

基于式（1）对噪声图像的定义解析小波阈值去噪的思路：第一步，基于小波变换法处理f(i，j)生成小波系数γi，j；第二步，定义不同分解层次的阈值，在获得估计小波系数前对原始小波系数进行阈值处理；第三步，重构小波系数，将小波估计系数作为依据构造崭新的去噪图像，完成图像精准去噪。

相比传统软硬阈值选取方法而言，小波阈值选取的动态调整性使其更精准的选取适合当前噪声处理的阈值［4］，公式（2）通过增加系数b实现了对小波阈值的自适应动态修正：

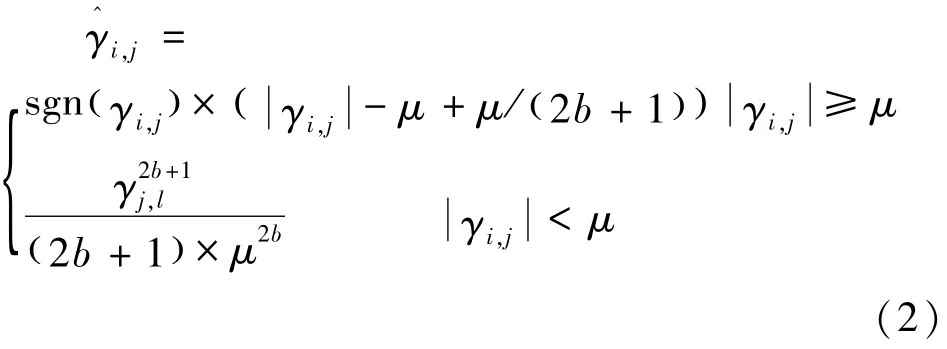
公式中，μ表示阈值，为b阈值调节系数；尤其是当时＜μ，基于非线性函数一步步压缩小波阈值，没有直接将零作为阈值函数，解决了直接降低阈值导致的图像去噪效果骤减问题，并且实现了阈值函数不间断呈现，具有良好的图像去噪效果。

2.2 基于粒子群算法的小波去噪阈值选取

粒子群算法是在空间中寻得最优解的高效率算法，在参数寻优领域应用广泛，粒子群算法使用适应度函数评判解的好坏，以迭代的方式逐步获得最优解。因此，小波阈值去噪算法的阈值可以视为在解空间中获得最优解的问题，为此基于粒子群算法选择小波最优阈值。各个粒子在解空间中的方向与位置是不断变化调整的，逐步获取最优解，调整的依据是粒子个体或者群体目前搜索的最优解情况。粒子群算法的编码思想以及粒子在空间搜索中的位置、速度等参数计算方法详见文献［5］。

以均方误差作为粒子群优化小波阈值的适应度函数，具体形式为：

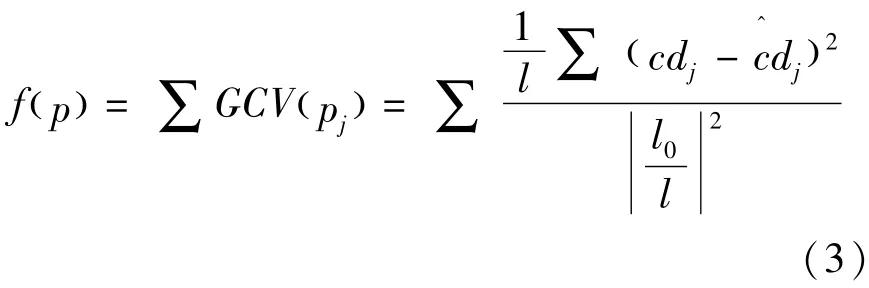
式（3）中，第j层阈值与小波系数总量分别采用pj、l表示；阈值函数处理第j层小波系数后归0的系数数量为l0；小波系数被阈值函数处理后的矢量形式为。

编码小波阈值的解、获得适合的适应度函数、寻优迭代是小波最优阈值确定的三个主要步骤，由此总结基于粒子群算法优化小波阈值的过程如下：

Step 1：编码完成的小波阈值即为粒子群算法中粒子的矢量位置信息，设置搜索空间维数为m，即小波分解的层数，每一层小波的阈值则为粒子在各个维度中的位置信息；选取空间内的任意数值作为解，并将其作为原始小波阈值。

Step 2：定义X表示观测信号，并对其实施小波分解处理，将以此刻粒子阈值作为阈值处理的依据，则为处理后得到的第i个粒子相应的小波系数矢量值，基于公式（3）计算粒子的适应度值［6］。

Step 3：确定个体最优与群体最优解，将此刻阈值视为粒子个体最优，当适应度值即均方误差最小时将对应的解视为群体最优解。

Step 4：粒子在解空间中的速度与位置信息需要进行持续更新，同时循环操作Step 2与Step 3，不断获得个体最优与群体最优值。

Step 5：不断执行Step 4中的内容当迭代次数达到上限时终止，或者迭代差值在规定范围内时终止迭代。

基于上述步骤粒子群算法最终获得一个最优的小波阈值，然后基于最优小波阈值以及公式（2）描述的小波阈值函数对图像实施小波去噪，大幅度降低图像的高斯白噪声，为图像边缘检测提供良好的基础条件。

2.2 基于梯度的图像边缘检测

图像边缘检测的方法众多，依据图像处理需求差异可以选取不同的算法进行图像处理。例如小波变换算法检测图像边缘具有良好的抗噪性能，但缺点是计算量大，延长了图像处理的时间开销；梯度算法用于图像边缘检测虽对噪声比较敏感，图像自身噪声降低了算法提取边缘信息的准确度，但是计算量相对较小边缘检测效率高［7］。综合以上算法性能分析，文章为降低图像边缘检测的计算量，首先基于小波阈值去噪滤除图像固有噪声，然后基于梯度算法检测图像边缘信息，基于梯度的边缘检测算法流程如下。

图像边缘点位置信息可通过求取图像的梯度获取，利用一阶导数描述梯度，因此在一幅图像中梯度的数学表达式如下：

其中，水平与垂向两个方向的梯度分量采用Mx、My表示。那么公式（5）、（6）为梯度幅值与方向的计算方法：

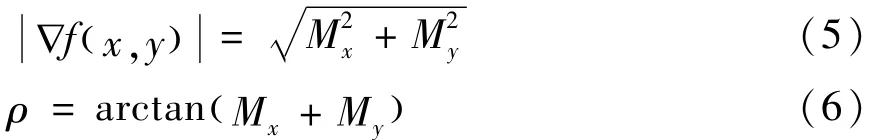
由此得到图像中相邻位置上两个像素之间的梯度差值计算方法：

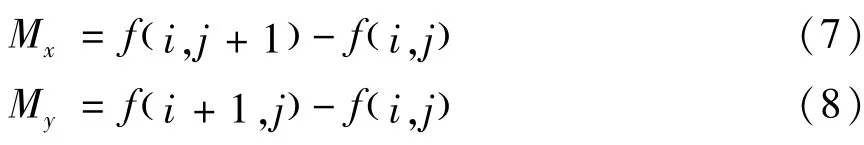
总体而言，基于梯度的图像边缘检测算法易于实现、步骤简单，文章使用改进小波阈值去噪法滤除图像噪声后，基于梯度算法来完成图像边缘信息检测。

3 算法测试与分析

为验证本文算法检测图像边缘信息的有效性与优势，在Matlab 2016平台上搭建算法测试环境展开图像检测仿真测试。选取50幅大小为512×512的图像作为去噪与边缘检测的测试集，将图像去噪的高斯噪声方差值设置为0.03，变换小波分解层数k为2、3、4、5、6，测试不同小波层数下本文算法的去噪效果，以确定最优的小波层数。实验选取基于小波变换的边缘检测算法、传统梯度边缘检测算法作为对比方法同时进行性能测试。

3.1 本文算法小波去噪层数确定

图1（a）为原始噪声图像，本文算法中不同小波分解层数对应的图像噪声去除结果如图1（b）～图1（f）所示。

图1 小波去噪效果

由图1可知，小波分解层数取值为2、3、4时的去噪效果较为理想，噪声含量明显降低。具体而言，当小波分解层数取值为2时图像噪声虽然大量减少，但是蓝莓果果实部分细节消失，表面较为光滑不利于图像边缘特征提取；当小波分解层数取值为3时的去噪效果最优，且保留了大量细节信息；当小波分解层数为4时画面整体具有模糊感，图像失真严重。综上所述，确定本文算法的小波分解层数为3，据此进一步展开图像边缘提取实验。

3.2 边缘检测效果分析

以3.1小节的图像作为边缘检测对象，采用三种算法同时提取蓝莓果实的边缘信息，边缘检测结果如图2所示。

图2 边缘检测结果

图2中，传统梯度边缘检测算法检测结果中冗余边缘信息较多，且蓝莓果实形状表现不完整；基于小波变换的边缘检测算法检测结果也不理想，虽然冗余边缘信息减少了，但是最下端蓝莓的圆形表达不完整，左侧两个蓝莓轮廓融为一体，没有明显的界线分割。相比之下，文章算法检测的蓝莓边缘信息较为精准，既能表达果实的基本内容，也没有冗余的边缘信息堆积，图像边缘检测效果较为理想。主要是因为文章使用改进小波阈值算法去除图像噪声，降低了梯度算法检测边缘的难度，优化了边缘检测效果。

4 结论

经仿真实验验证，该研究取得了较优的图像去噪效果以及边缘检测效果，相比基于小波变换的边缘检测算法、传统梯度边缘检测算法而言，文章算法检测边缘信息的精度最高，可以表达图像中蓝莓果实的基本内容且不需要堆积冗余的边缘信息。随着未来数字图像分析要求的提高，需要不断优化图像边缘检测效果。在以后的研究中可从梯度检测算法入手，改进梯度幅值与方向的确定方法，以获取更为精准的梯度检测效果。