改进的突然对称扩散水跃方程
2020-03-30宁利中宁碧波田伟利渠亚伟
宁利中,张 珂,宁碧波,田伟利,渠亚伟
(1.西安理工大学, 陕西 西安 710048; 2.嘉兴学院, 浙江 嘉兴 314001;3.上海大学, 上海 200444)
泄洪消能是我国水利枢纽工程建设中的关键性技术问题。根据有关实际工程资料统计,其造价约占工程总造价的40%~50%。因此消能防冲设施十分重要。在整个过程中,消能是主要手段,防冲是辅助措施。对于具体的水流条件、地形地质条件、泄水建筑物的形式与布置等,如何才能够提供一个有效的高消能效率区,这是人们解决各种泄洪消能问题的关键。对于不同的泄洪消能形式,虽然具体的消能防护控制标准或设计准则不尽相同,但解决问题的基本途径是一致的。水跃的研究长期受到学者的关注[1-8]。
最简单的情况是水平渠底等宽二元渠道中的水跃。Belanger于1928年忽略能量损失应用能量方程建立水跃方程,没有成功,10年后,他改用动量方程给出了二元渠道中的水跃共轭水深比的显式解。最近几十年,由于工程建设的需要和技术手段的进步,对水跃的研究有了较大的发展。由于消力池的几何形状取决于地形的条件,经常被布置为扩散式。从而引起了学者对扩散水跃的研究。扩散水跃可分为水平渠底渐扩明渠段中的水跃[9-13]和突然扩散段中的水跃[14-21]。文献[15,17-18]对突扩式水跃进行了实验。郭子中[1]在用动量方程计算共轭水深时忽略了始端突然扩大壁面压强的影响,后来发现始端突然扩大壁面平均水深的影响较大,引入各种假设[14,19-21],用动量方程计算共轭水深时仍然存在误差。因此,搞清楚始端壁面平均水深已经成为保证利用动量方程计算共轭水深精度的关键。最近,又有学者[22-24]就渐扩消力池水力特性进行了研究。本文通过分析,研究了突然对称扩散水跃共轭水深的水力特性。发现突然对称扩散水跃始端扩散断面的回流平均水深h3可以表示为跃前断面水深h1和跃后断面水深h2的函数。根据大量实验资料,给出了回流平均水深表达式中系数α随着突扩比β变化的函数关系式。根据动量原理建立了突然对称扩散水跃共轭水深方程。本文建议的方程能够很好的与实验吻合一致。在已有的计算方法中,本文方程与实验结果的平均误差和最大误差最小。因此,本文方程可以应用到实际问题的水力计算。
1 回流平均水深
图1是水平底突扩式水跃的流动示意图。h1、h2为跃前、跃后断面水深,h3为回流区平均水深,b、B为上游、下游渠槽宽度。按照图1的流动示意图通过动量原理建立水跃方程时必须考虑始端水深,如图2所示。

图1 突扩式水跃示意图

图2 突扩断面回流区水深示意图

h3=h1+αh2
(1)

α=-0.0512β2+0.3267β-0.0653
(2)
将式(2)代入式(1)就确定了回流区平均水深。显然,式(1)既反映了跃前断面水深,跃后断面水深对回流区平均水深的影响,也反映了突扩比β对回流区平均水深的影响。

图3 系数α与突扩比β的关系
2 突然扩散水跃的共轭水深方程
对于图1的流动进行分析时假定:
(1) 跃前与跃后两断面上的水流为渐变流。
(2) 忽略摩擦阻力。
基于上述假定,对图1的跃前与跃后两断面在流动方向应用动量原理,有
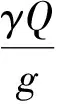
(3)
式中:Q为流量,γ为水的重度,g为重力加速度,v1、v2为跃前、跃后断面的平均流速,α01、α02为跃前、跃后断面动量修正系数,P1为跃前断面的动水总压力,P2为跃后断面的动水总压力,P3为水跃始端扩散断面上的动水总压力。
根据假定(1),动水压力服从静水压力分布,则
(4)
(5)

(6)
根据连续性原理,有
Q=v1h1b=v2h2B
(7)
考虑假定(2),有
α01=α02=1.0
(8)
将式(4)至式(8)代入式(3),得
(9)
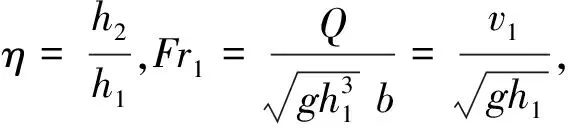
(10)
式(10)即为改进回流平均水深假设条件下突然扩散水跃的共轭水深方程。
3 突然扩散水跃方程(10)的验证
方程(10)可以通过迭代法或者试算法求解。由于计算机的普及,方程(10)可以很快通过迭代法求解。方程(10)的计算结果与文献[17,20]实验结果的比较如图4所示。

图4 方程(10)的计算结果与实验结果的比较
不同突扩比情况下方程(10)的计算结果与文献[17,20]实验结果的误差分析如表1所示。由表1可以看出,最大平均误差发生在β=3.0的情况下。最大误差发生在β=2.0的情况下。

表1 不同突扩比时计算结果与实验结果的误差
对于不同假定情况下理论方程的计算结果和文献[17,20]实验结果的的平均误差和最大误差分析如表2所示。可以看出,文献[19]理论方程的计算结果平均误差和最大误差最大。文献[14]理论方程的计算结果平均误差次之。文献[20]理论方程的计算结果最大误差次之。本文理论方程(10)的计算结果平均误差为6.105%,最大误差是25.767%。在已有的研究成果中,本文方程与实验结果的平均误差和最大误差最小,精度最高。因此,本文方程可以应用到实际工程的水力计算。

表2 不同方程计算结果与实验结果的误差
4 结 论
(1) 突然对称扩散水跃始端扩散断面的回流平均水深h3可以表示为跃前断面水深h1和跃后断面水深h2的函数,即h3=h1+αh2。根据大量实验资料,系数α可表示为突扩比β函数,其关系式为:
α=-0.0512β2+0.3267β-0.0653。
(2) 根据动量原理建立了突然对称扩散水跃共轭水深的理论方程,方程的形式为:
(3) 突然对称扩散水跃共轭水深方程的计算结果与实验结果的比较说明,本文给出的方程能够很好的与实验吻合一致。在已有的研究成果中,本文方程与实验结果的平均误差和最大误差最小。因此,本文方程具有较高的精度,可以应用到实际问题的水力计算。
