超音速悬索火箭橇水平运动偏差仿真分析*

游培寒,赵未平,白晨阳,祝逢春

(1 北京航空工程研究中心, 北京 100076； 2 南京林业大学， 南京 210037)

0 概述

悬索火箭橇[1]是一种约束弹道试验装置，可用于测试空空武器的近炸引信等需要高速精确定向飞行的相关设备。如图1所示，它利用两根平行布设并拉紧的悬空索道作为滑轨，约束火箭橇体于两根悬索中间，发动机推动火箭橇在悬索约束下定向运动。橇体定向飞行控制精度是悬索火箭橇系统设计的难点，文献[2]分析了橇体飞行过程对悬索的下拉作用，文中通过有限元建模仿真方法分析了侧风大小、悬索初始拉力和悬索弹性模量对飞行橇体水平偏移的影响。

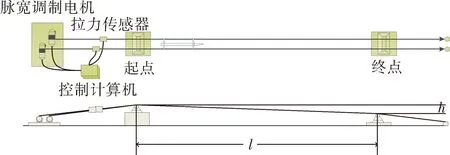
图1 悬索火箭橇

首先介绍利用Newton法对悬索进行3D运动建模；接着介绍了火箭橇橇体运动建摸和火箭橇运动有限元计算方法；然后介绍有限元建摸仿真分析得到的侧风大小、悬索初始拉力和悬索弹性模量对橇体水平运动控制精度的影响；最后给出结论。

1 基于Newton法的悬索运动建模

橇体飞行的水平偏移主要因为悬索的弹性应变造成，这种弹性应变还会引起橇体在垂直方向的下拉运动，所以必须在3D空间中对悬索进行运动建模，这里用Newton法对悬索运动建摸[3],公式如下：

(1)

(2)

(3)

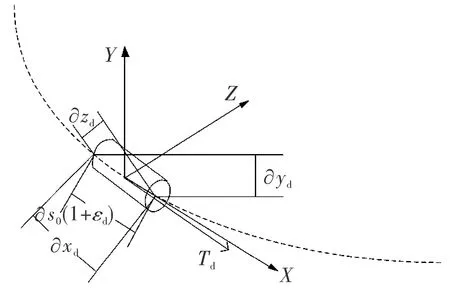
图2 悬索微元的受力分析

X、Y、Z分别代表悬索单位长度在x、y、z轴3个方向的外力，当悬索微元不处于火箭橇位置时在x方向并不受力有：

ifk≠r,Xk=0

(4)

k为悬索微元序号，r为火箭橇运动位置。

y方向受力主要来自索道本身的重力有：

ifk≠r,Yk=0

(5)

Z主要来自于索道自身受到的侧向力，有：

(6)

式中：cz为悬索的侧向阻力系数；Az为悬索静态单位长度对应的悬索动态侧向截面积；d为悬索直径；vz为侧向风速；ρ为空气密度。Td,k为悬轴第k个微元的动态拉力[4]有：

Td,k=T0+Eεd,kAx

(7)

其中Ax为悬索横截面积；E为悬索的弹性模量；T0为悬索的初始拉力；εd,k为第k个微元的应变。

2 火箭橇体运动建模

前期试验表明橇体飞行过程中姿态变化很小，可以将橇体简化为一个运动质点，橇体轴向方向始终与悬索方向一致，橇体位置的悬索在y方向和z方向与橇体一起运动，在y方向有:

Td，kcosβd,ksinαd,k)-(mr+m∂s0)g+

(P-Nmr-Γ)·cosβd,ksin(αd，k-αd,k+1)

(8)

其中：yd,r为橇体在y方向的动态坐标;yd,k为悬索微元在y方向的动态坐标;P为火箭橇发动机的推力;N为摩擦力系数；αd,k为悬索第k个微元轴向与x方向的夹角在xy平面的映射：

(9)

βd,k为第k个微元轴向与x方向的夹角在xz平面的映射：

(10)

mr为橇体质量:

(11)

式中：m0为橇体的初始质量;mP为发动机装药质量;TP为发动机的工作周期;Γ为橇体的轴向空气阻力[5]:

(12)

式中:cr为橇体轴向空气阻力系数；vr为橇体飞行速度；Ar为橇体轴向截面积。

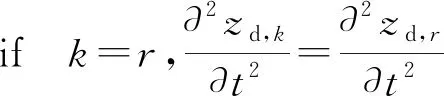
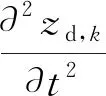
(P-Nmr-Γ)cosαd,ksinβd,k

(13)

式中：zd,r为橇体在z方向的动态坐标；zd,k为悬索微元在z方向的动态坐标；crz为橇体侧向空气阻力系数；Arz=ldr为橇体侧向截面积；l为橇体长度；dr为橇体直径。

在x方向由于橇体在悬索上滑行，悬索只给橇体一个摩擦阻力，所以在x方向橇体运动模型为：

ifk=r

(14)

xd,r为橇体在x方向的动态坐标。而悬索微元只受到橇体的摩擦力，可以近似认为在x方向悬索微元的运动模型为：

ifk=r

(15)

xd,k为悬索微元在x方向的动态坐标。橇体运动建模中受力分析参考图3所示。

图3 橇体运动受力分析

3 悬索火箭橇运动有限元计算方法

第二步确定有限元计算的时间步长。时间步长应保证微元计算速度高于悬索波速vb的两倍，即[1]：

(16)

第三步设定边界条件。火箭橇运动过程中，索道两端固定不动，即：

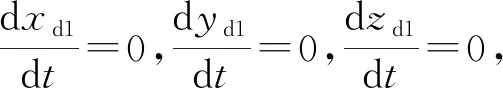
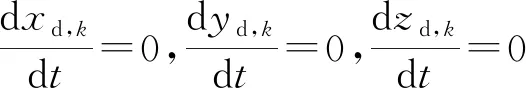
(17)

第四步设定初始条件。设定初始悬索拉力T0，设定初始侧风速度vz;设置悬索微元的初始坐标有：

z0,k=0k=1,…,K

(18)

同时各微元的动态速度为零。

(19)

H为悬索两端高度差。选择悬索微元坐标为火箭橇初始位置，比如橇体初始位置在第10个微元位置则有：

r=10,x0,r=x0，10,y0,r=y0，10,z0,r=z0，10

(20)

第五步进行迭代计算。采用龙格库塔法迭代计算悬索K个微元的位置、速度和加速度[2]。其中当k≠r时，采用式(1)～式(7)计算加速度，然后计算各点的速度和位置变化；当k=r时，采用式(8)、式(13)、式(15)计算该点的加速度，进而推导出速度和位置变化。然后利用式(8)、式(13)、式(14)计算橇体的加速度、速度和位置，用橇体位置距离最接近的悬索微元序号更新橇体位置r。如此反复直至橇体运动至悬索末端为止。

4 火箭橇水平运动控制精度分析

以国内某超音速悬索火箭橇试验系统的相关参数为计算依据，分析侧风、初始拉力和悬索弹性模量对橇体水平运动控制精度的影响。索道长度为280 m，索道起点比终点高出5 m，悬索单位长度质量m=0.039 kg/m，悬索的弹性模量E=3.4×109Pa/m，悬索的侧向阻力系数cz=0.6，悬索直径d=0.008 m。索道设计初始拉力T0=2 400 kg。

橇体采用改进的70 mm火箭弹发动机制成，其初始质量m0=10.36 kg，装药质量mP=3.6 kg，发动机工作周期TP=0.65 s，发动机的平均推力P=10 000 N，橇体的轴向空气阻力系数cr参考文献[4]查表拟合得到，橇体轴向截面积Ar=0.003 8 m2；橇体侧向空气阻力系数crz=0.65，橇体长度l=1 m，橇体直径dr=0.07 m。橇体的初始位置r=10。

对悬索进行网格划分，单个悬索微元长度为∂s0=1 m，共划分出281个悬索微元。龙格库塔法迭代计算的时间步长为Δt=10-4s。

为了简化问题,下面的仿真分析做了以下假设：一是两根平行布设的悬索特性参数和运动状态完全相同。二是侧风方向与索道方向垂直，侧风风场均匀分布,速度恒定。三是设悬索与橇体之间的摩擦恒定。

4.1 侧向风大小对水平运动控制精度的影响

侧风是造成火箭橇水平偏移的主要原因。在近期进行的火箭橇发射试验中实际测得侧风风速为4 m/s，火箭橇成功穿过了一个布设距离终点5 m、宽度大于橇体宽度0.01 m的缝隙，说明在这里橇体的水平运动控制精度在0.01 m以内。下面部分分析橇体水平控制精度与侧风风速之间的关系。

设侧风风速vz=5 m/s(3级风)，火箭橇发射后0.05 s、0.2 s、0.4 s、0.6 s、0.76 s时水平偏移如图4所示，图中圆圈代表橇体飞行位置，由图可见在橇体发射后0.4～0.6 s，橇体的水平偏移最大达到0.06 m，但随着橇体接近终点水平偏移又逐步缩小。

图4 侧向风速为5 m/s时火箭橇发射后的橇体偏移

图5是发射后0.68 s、0.70 s、0.72 s、0.74 s、0.76 s时的橇体偏移。如果侧向风速5 m/s时要求火箭橇在着靶瞬间其水平控制精度不大于0.01 m，则靶标与终点的距离应小于22 m。

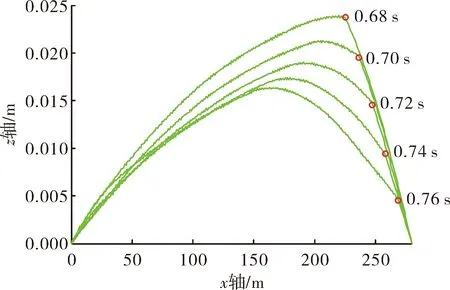
图5 侧向风速为5 m/s时火箭橇发射后的橇体偏移

图6是风速为5～10 m/s时，也就是从3级风到5级风情况下，橇体发射后0.76 s时的橇体水平偏移。可以看出当靶标设置在距离终点10 m处时，在风速小于7 m/s时，能够保证水平控制精度不大于0.01 m。

图6 侧向风速为5～10 m/s时火箭橇发射后0.76 s时的橇体偏移

综合以上分析，为了保证火箭橇飞行末端的水平控制精度不大于0.01 m，侧风速度应不大于7 m/s，同时靶标与终点距离应小于10 m。

4.2 悬索初始拉力对水平运动控制精度的影响

图7绘制了侧风vz=5 m/s时，不同初始拉力情况下，火箭橇发射0.5 s后橇体的水平偏移。圆圈对应橇体位置，橇体偏移最小的对应初始拉力T0=2 600 kg，橇体偏移0.05 m；橇体偏移最大的对应初始拉力T0=2 000 kg，橇体偏移0.75 m。

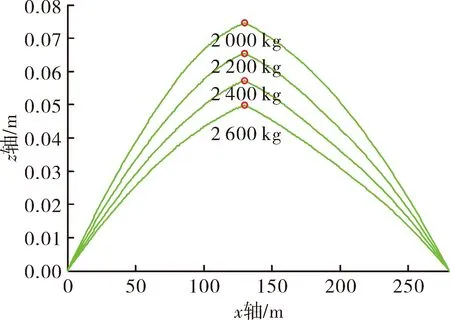
图7 侧向风速为5 m/s时，不同悬索初始拉力下火箭橇发射0.5 s时橇体的水平偏移

图8绘制了侧向风选为5 m/s时，不同初始拉力情况下，橇体发射后0.76 s，也就是飞行至距离终点约10 m处橇体的水平偏移，偏移最小的对应T0=2 600 kg，橇体偏移0.003 7 m；偏移最大的对应初始拉力T0=2 000 kg，橇体偏移0.006 9 m。

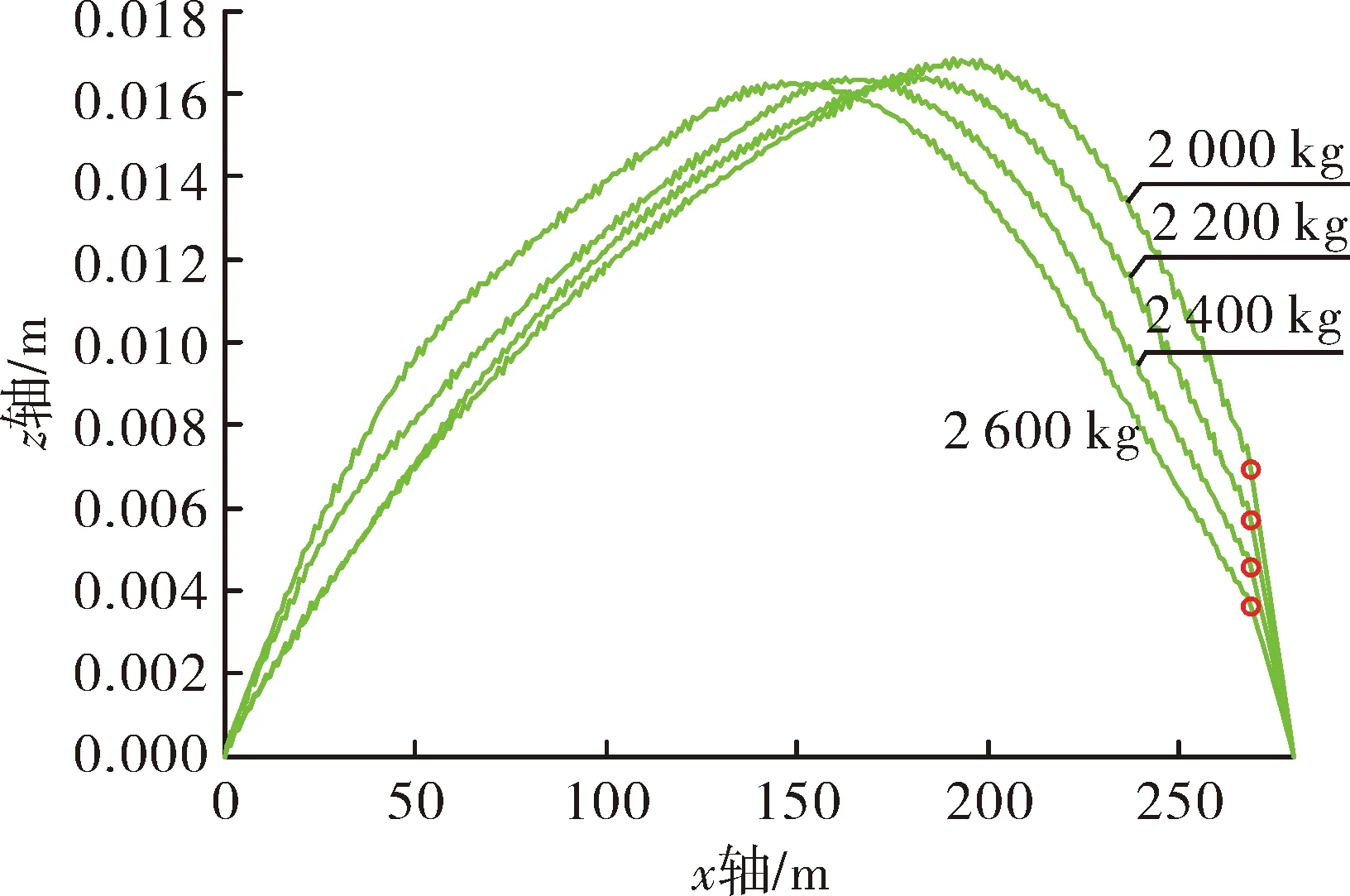
图8 侧向风速为5 m/s时，不同悬索初始拉力下火箭橇发射0.76 s时橇体的水平偏移

初始拉力大可降低橇体飞行过程中的水平偏移。但是初始拉力较高会提高系统的设计成本；综合以上分析，在保证末端水平控制精度小于0.01 m情况下，设计初始拉力应大于2 000 kg。

4.3 悬索材料弹性模量对水平运动控制精度的影响

悬索的弹性模量与材料纤维粗细、盘结方式等因素有关，根据前期测试悬索材料的弹性模量会在一定范围内变化，以下分析悬索弹性模量变化对橇体飞行控制精度的影响。图9是弹性模量E=2.0×109Pa/m、3.4×109Pa/m、5.0×109Pa/m、6.5×109Pa/m时，初始拉力T0=2 400 kg，火箭橇发射0.5 s后橇体的水平偏移，可见偏移量差别也不大，约为0.057 m。

图9 不同悬索弹性模量条件下橇体的水平偏移

所以当初始拉力较大时，悬索弹性模量差异对橇体的水平偏移影响可以忽略。

5 结论

利用Newton法对悬索进行3D运动建模，并结合橇体运动建模进行有限元仿真计算，分析了侧风、初始拉力和悬索弹性模量等参数对橇体水平运动控制精度的影响；结果表明，监测试验场地的实时风速，提高悬索初始拉力都有利于减少橇体运动的水平偏移。2018年年底进行的某型超音速悬索火箭橇飞行试验结果表明，本方法计算得到的橇体水平偏移数据与现场测试结果相吻合，说明方法的有效性。