某大型制导火箭弹发射动力学仿真与试验分析*

刘馨心,袁 野，周昌盛,麻小明,胡建国,李 庚

(1 西安现代控制技术研究所, 西安 710065； 2 32381部队， 北京 100072)

0 引言

大型制导火箭弹质量大、发动机推力强、试验成本昂贵,对发射装置造成的振动可能使仪器和构件的正常工作受到干扰,为确保地面发射装置能够可靠发射,需要在设计初期和试验前对整个发射系统进行发射动力学仿真计算,以保证在动载作用下结构的安全、经济及使用性能,使导弹的发射精度和可靠性符合要求。文献[1]针对导弹离轨安全性问题,建立了考虑弹性的导弹倾斜发射动力学模型,通过算例研究了导弹离轨动力学模型的可行性;文献[2]运用ADAMS及有限元软件建立某车载倾斜发射装置刚柔耦合模型,重点对发动机推力偏心及闭锁力扰动因素进行了仿真分析。目前大多数相关研究主要以理论计算或仿真为主,没有进行试验验证。文献[3]建立了由适配器支撑的地空导弹发射动力学模型,对比了发射过程俯仰角仿真与试验曲线,但是该模型仅建立了发射筒、适配器和弹体,并未考虑发射装置的弹性作用。

文中基于多体动力学软件ADAMS搭建刚柔耦合动力学模型,仿真计算制导火箭弹发射过程中弹体初始扰动、质心下沉量、发射导轨动态响应等参数,同时结合地面发射试验,验证模型的准确性,为制导火箭武器系统的论证研制提供参考。

1 发射动力学数学模型

1.1 动力学方程建立

构件Bi在惯性空间作一般运动,其动能的坐标形式为[4]:

(1)

式中:ri是构件Bi质心速度在惯性基(e0)中的坐标列阵;ωi是刚体角速度在连体基(ei)中的坐标列阵;mi是刚体的3×3质量对角阵;Ji是刚体对质心的惯性张量在连体基(ei)中的惯量矩阵。将ωi的欧拉角表达式代入式(1),刚体动能的欧拉角表达式为:

(2)

定义系统的笛卡尔广义坐标为:

(3)

系统所受约束方程为:

(4)

对每个刚体Bi写出对应于6个广义坐标的6个拉格朗日方程:

(5)

(6)

将以上的方程合并成以下矩阵形式:

(7)

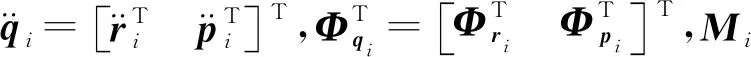
将系统的n个刚体的n个方程式写成统一的矩阵方程,并和系统的约束方程联立可得系统动力学方程为:

(8)

1.2 子结构模态综合法

对于刚柔耦合多体系统,可将柔性体视为子结构,利用结构动力学的模态综合技术,使用少量的模态坐标作为广义坐标来缩减系统方程的自由度,降低求解规模[5-6]。

考虑具有约束界面的系统子结构,运动方程为[7]:

(9)

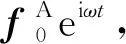
(10)

按界面(m)自由度与内部(s)非界面自由度分块形式,运动方程又可写为:

(11)

2 动力学仿真分析

2.1 动力学模型

发射系统由发射平台、回转体、电动油缸、起落架、导轨安装架、导轨和导弹组成。其中发射平台、回转体、起落架和导弹为刚体,发射方式为同时离轨,导轨设计为阶梯型,并将导轨视为弹性体,由ADAMS内部柔性化模块将原本的刚体导轨转化为柔体,转化后的节点数为113 903,截取的有效模态数为30阶,其固有频率范围:26.1～13 976.5 Hz。导轨材料弹性模量2.07×1011Pa,泊松比0.29,密度7.801×10-6kg/mm3。

系统总体坐标系为:X轴沿弹轴指向导弹发射方向,Y向垂直于弹轴向上,Z向由右手定则确定。

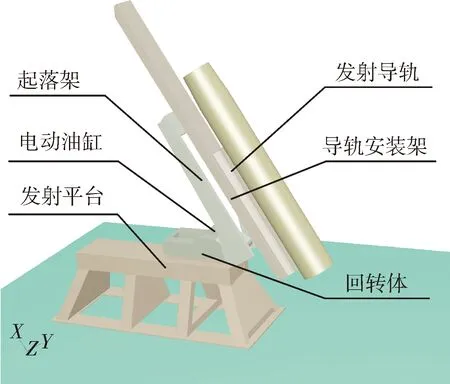
图1 动力学模型

2.2 模型约束定义

各个部件之间的连接关系为:

1)发射平台与大地用固定副固结。

2)回转体与发射平台用固定副固结。

3)起落架与回转体在耳轴处用旋转副连接,使起落架可以绕耳轴相对发射平台和回转体在XY平面内做俯仰转动。

4)导轨与起落架在4个连接处分别用旋转副约束,使导轨相对于起落架的自由度为0。

5)导弹与导轨之间为接触约束,以模仿发射时导弹滑块与导轨之间的碰撞效果,由ADAMS内部的contact接触函数定义。

6)起落架与发射平台之间的电动油缸用弹簧阻尼器模拟,弹簧刚度为4.57×107N/m,阻尼为5.9 N·s/m。重力在沿电动油缸方向有分量,在弹簧阻尼器上施加预加载荷15 000 N。

7)推力数据采用总体提供的推力数据,仿真过程中用插值的方式加载到弹体尾端中心。

8)导弹燃气引起的附加载荷以集中力施加到起落架上。

2.3 模型输入条件

火箭弹外形尺寸由三维模型控制,弹重、质心位置、转动惯量等参数通过实测数据输入。火箭弹前后支撑滑块在弹体尾端完全离开导轨后分离,分离时产生的冲量根据实测数据添加;发动机推力曲线根据实测得到时间历程数据,通过ADAMS中AKISPL函数拟合得到发动机推力-时间曲线,并将该曲线施加于火箭弹尾部,发动机主推力偏斜20′,按照上下左右4种工况施加。

2.4 仿真分析与研究

为确保地面发射试验安全顺利进行,在试验前对试验工况进行仿真计算,仿真和测试结果见表1。

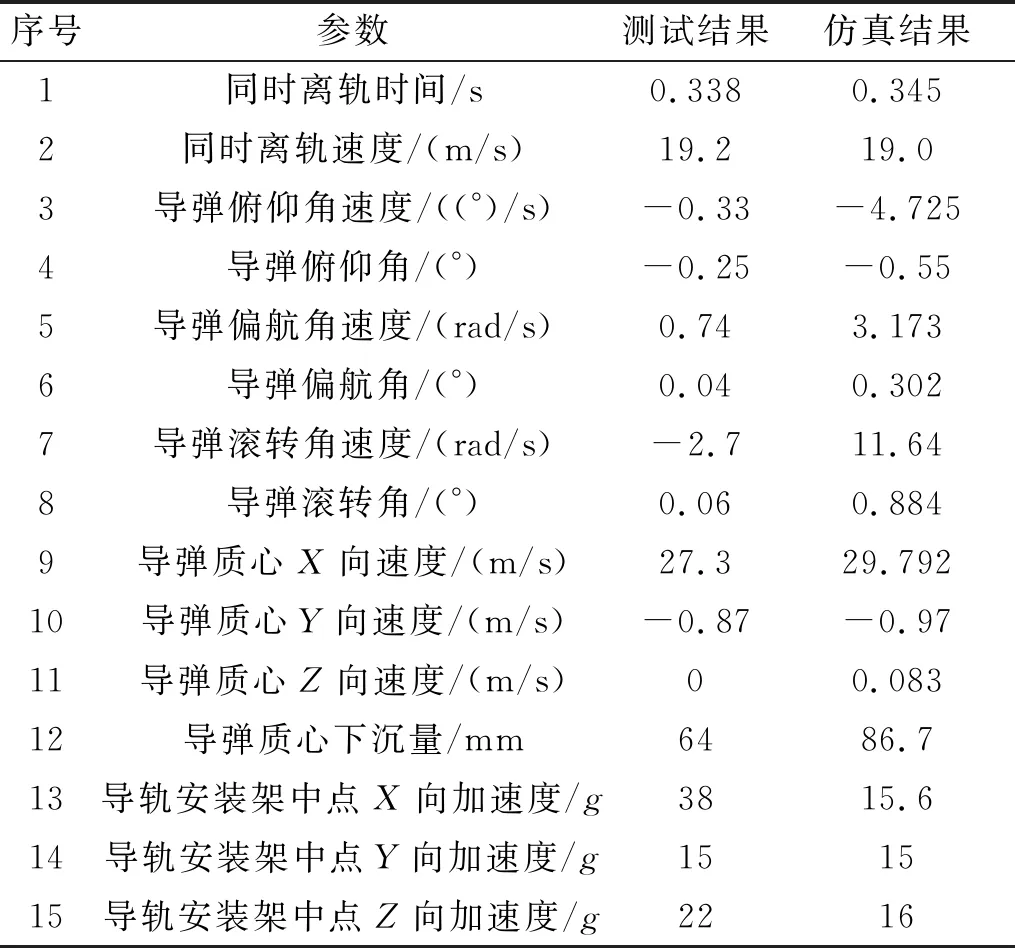
表1 发射动力学参数结果汇总

由表1中的数据可看出,弹上测试数据与发射动力学初始段的仿真计算结果基本一致,弹体姿态均在仿真结果的包络内,说明发射动力学的初始段仿真可信。

由于存在发动机推力线偏斜4种工况和弹体质心偏移4种工况的交叉共计16种工况,表1所示部分参数并非是在最恶劣工况下的结果,因此需要对发动机主推力上偏斜20′、质心下偏这一极限工况进行仿真计算,部分仿真结果如图2～图7所示。

图2～图4为弹体发射过程俯仰角速度、偏航角速度和滚转角速度时间历程曲线,根据仿真计算,弹体同时离轨的时间为0.345 s,弹体尾端完全离轨时间为0.523 s,前滑块分离时刻为0.55 s,后滑块分离时刻为0.61 s。

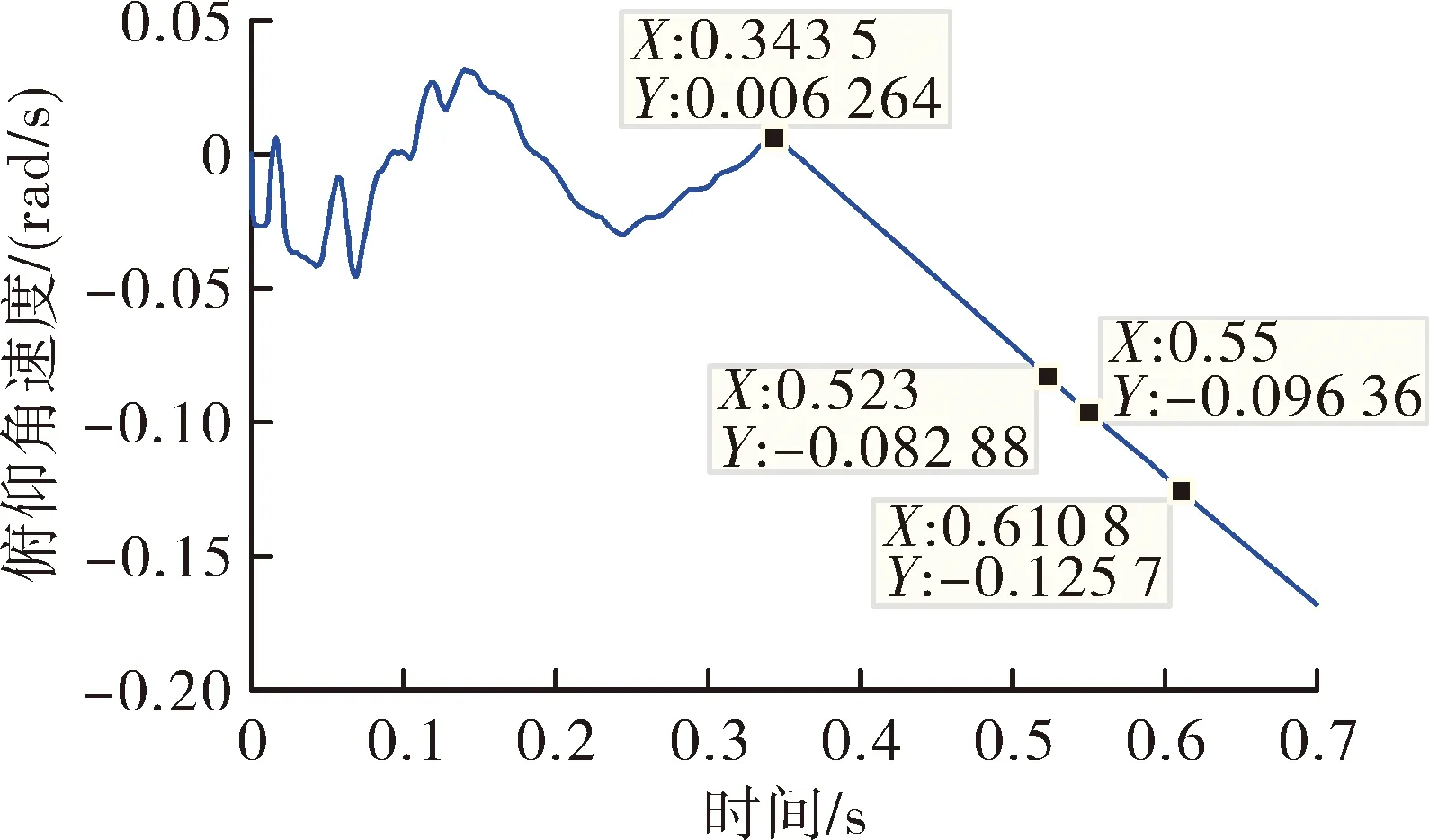
图2 弹体俯仰角速度曲线

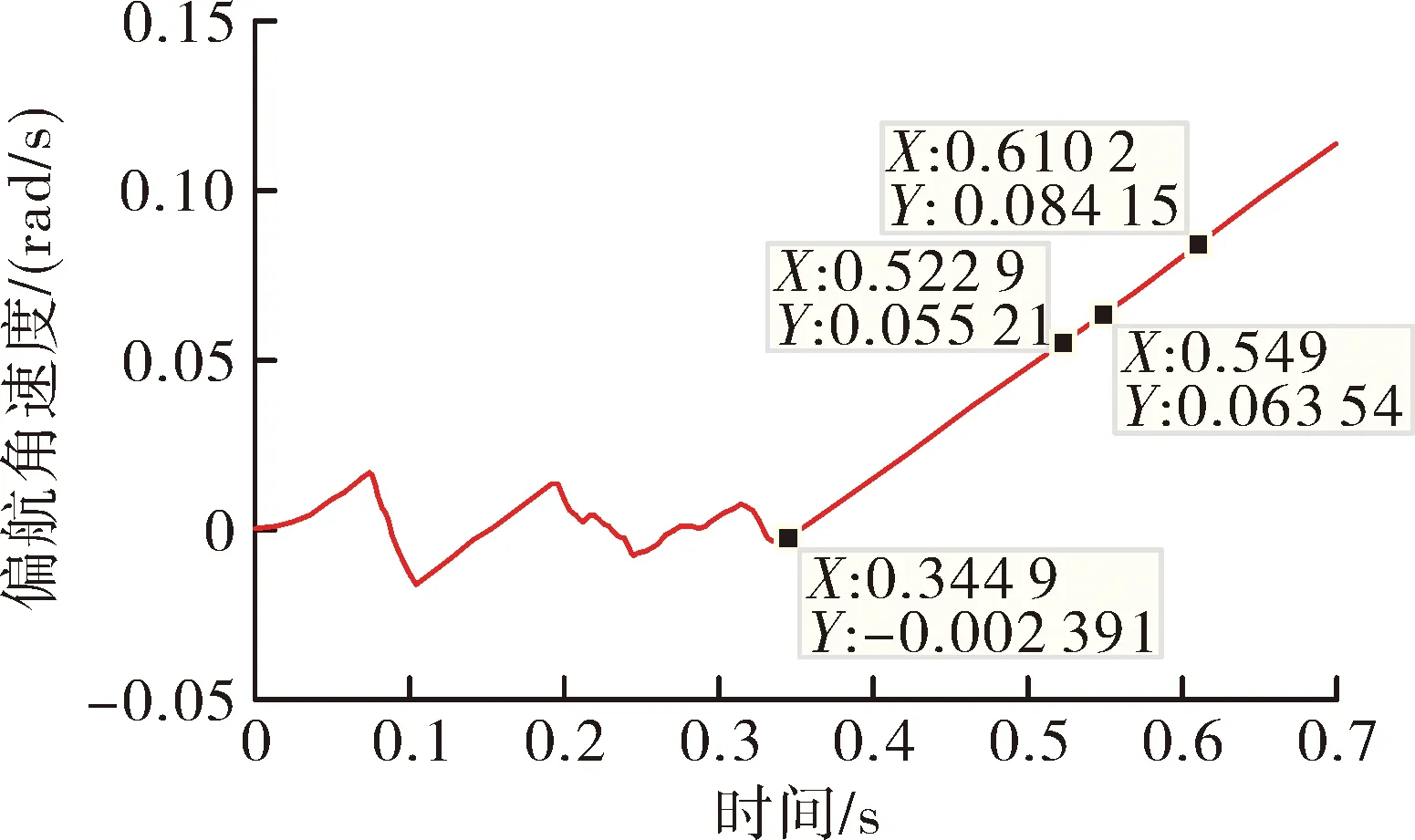
图3 弹体偏航角速度曲线

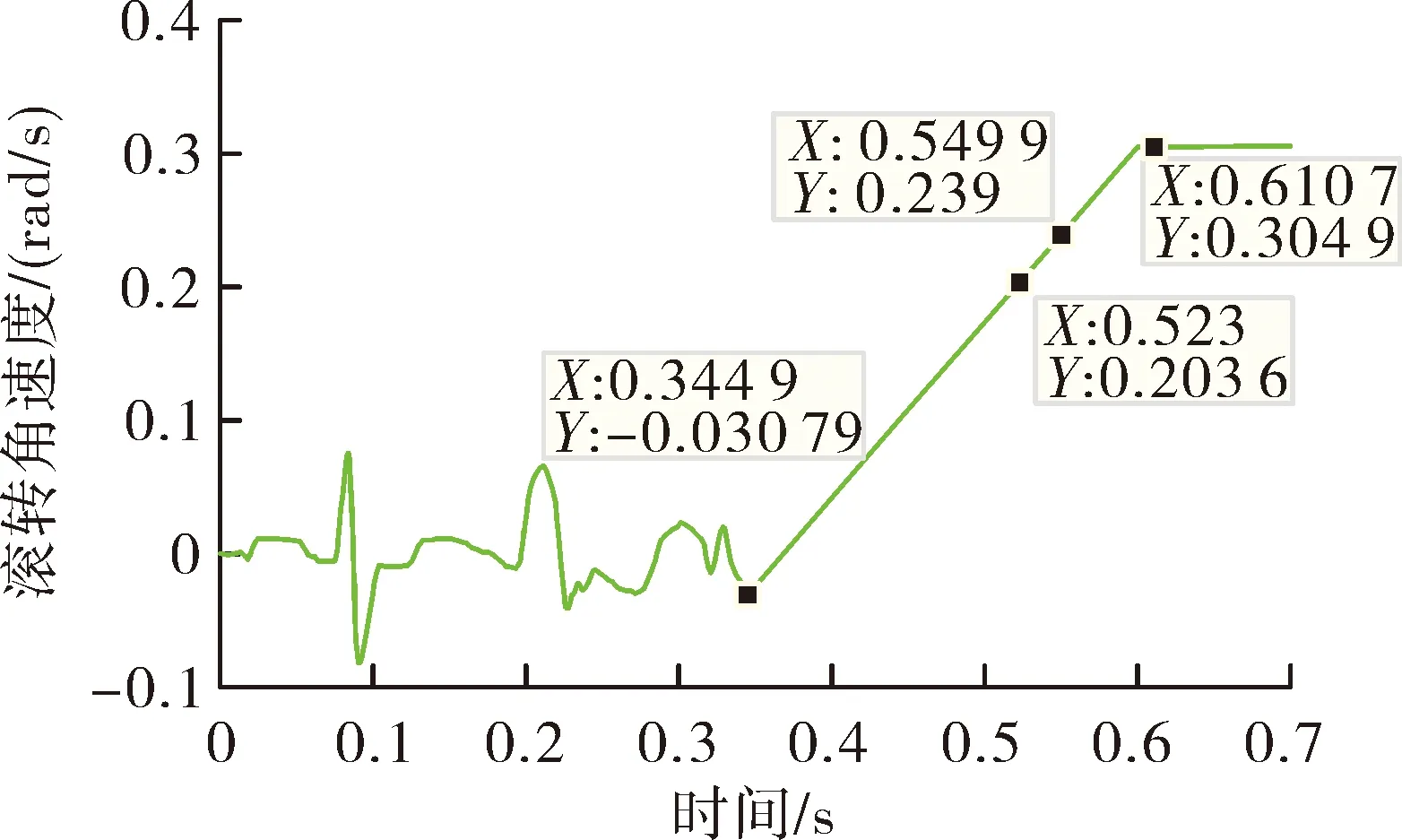
图4 弹体滚转角速度曲线

由图2～图4可以看出,弹体尾端完全离轨时弹体姿态角速度较小,后滑块分离时弹体俯仰、偏航、滚转3个方向的角速度分别为-0.126 rad/s、0.084 rad/s、0.305 rad/s,此时舵翼起控,发射初始扰动满足要求。

图5～图6为弹体质心和弹体后滑块垂直于导轨轨面方向的位移,方向向下为正,弹体尾端完全离轨时弹体质心沿导轨轨面法向移动了120.2 mm,同时后滑块沿导轨轨面法向移动了130 mm,均小于高低轨之间落差,弹体下沉过程中不会与导轨发生碰撞。

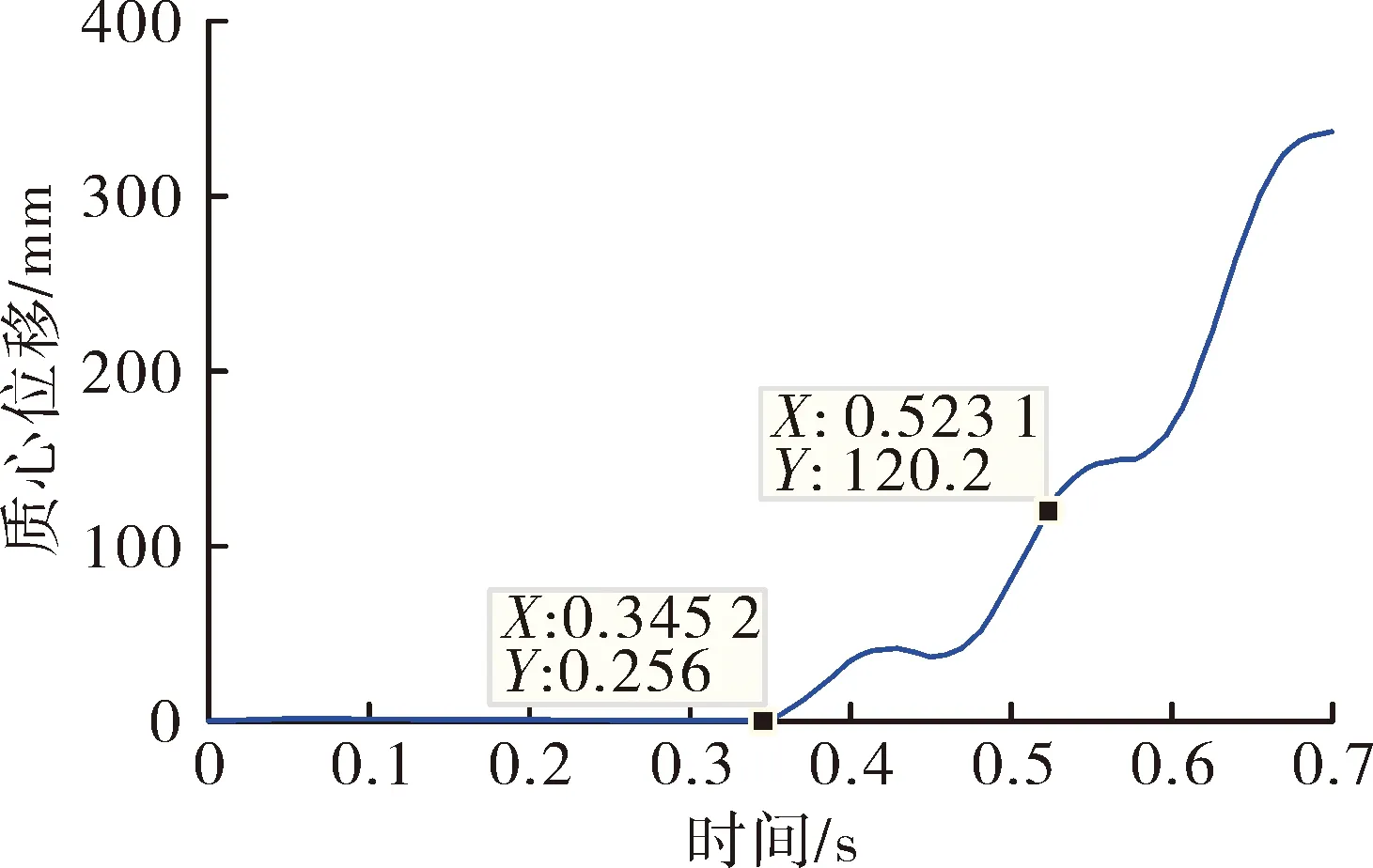
图5 导弹质心垂直于导轨轨面方向的位移

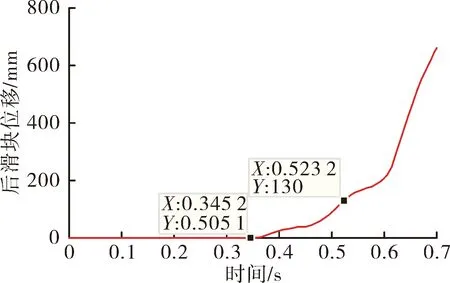
图6 导弹后滑块垂直于导轨轨面方向的位移

图7为导弹发射过程中导轨顶点位移时间历程曲线,由图中可以看出,弹体同时离轨之后,导轨顶点振动位移增大,差值为0.95 mm。

图7 导弹发射过程中导轨顶点位移时间历程

综合极限工况下的仿真结果可以判断出,弹体初始扰动、下沉量及导轨端点移动等均满足设计要求。

3 结论

仿真计算了某大型制导火箭弹发射过程中弹体及发射架的相关参数,并结合试验验证了模型的准确性,为项目研制提供有力参考。根据计算与试验结果可以得到以下结论:

1)最恶劣工况下,导弹从点火到弹体尾端完全离开导轨,弹体没有与导轨发生二次碰撞,发射初始段是安全的;

2)弹体初始扰动满足设计指标,在后滑块与弹体分离后舵翼起控,不会产生掉弹、失控等问题;

3)前后滑块在导弹离轨后先后与弹体分离,分离过程中前后滑块均不会与弹体发生碰撞;

4)导轨安装架X、Y、Z三个方向的振动加速度控制在38g、15g和22g以内,振动幅值较小,发射装置设计合理、可靠。