动机座发射条件初始参数误差对平台惯导影响评估*

王召刚，聂 凯

(大连92124部队， 辽宁大连 116023)

0 引言

在动机座发射条件下，平台式惯性导航输出地心系位置和速度参数的误差源有两个：一个是惯导平台制导工具误差，一个是惯导系统初始参数误差。初始参数误差是参数装订值与实际值的偏差,对纯惯性导航输出具有较大影响。这些参数包括原点位置误差、射向误差、调平误差、初始速度误差。初始参数一般由动机座载体提供。载体提供平台初始参数一般包括两个时刻：断调平时刻和发射时刻。断调平时刻载体位置和姿态是平台调平和射向初始参数装订的参照，其中平台姿态误差包括平台相对载体姿态误差和载体相对地理坐标系姿态误差两部分。发射时刻载体位置和速度是初始速度和初始位置装订值，是导航积分计算初始值。受载体测量误差影响，在计算惯性导航初始参数时存在较大系统误差[1]。断调平时刻的原点位置误差一方面以平台轴指向误差影响惯性导航位置速度输出，另一方面因为地球自转初速度而直接影响导航速度输出[1-2]。发射时刻原点位置以积分形式影响导航位置输出。初始速度的测量系一般是当地地理坐标系，测量误差在作为积分初始值影响速度同时还以积分形式影响位置。

文中首先推导利用惯性平台系测量参数计算地心系位置、速度参数公式。根据惯性导航误差累积性特点，把初始参数对导航的影响表示为关机时刻导航输出轨道与真实轨道的偏差。利用添加不同误差的初始参数，计算导航输出与真实轨道偏差评估初始参数对导航输出的影响；利用蒙特卡洛打靶法和绝对误差界[3]确定方法评估初始参数测量误差导致的关机时刻轨道位置和速度散布。通过这两种方式给出了初始参数误差对地心系导航参数影响的估计模型。

1 地心系导航参数计算模型

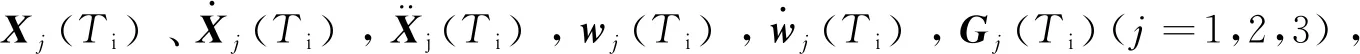
图1 平台姿态角{α,β,γ}示意图

由地心系到NUE的坐标变换矩阵为[4]：

(1)

式中：Rx、Ry、Rz分别为绕x轴、y轴、z轴正向旋转矩阵。

由理想惯性平台系向NUE系转换矩阵为：

C2=Ry(β)Rz(-α)Rx(-γ)

(2)

C=C1TC2为理想惯性平台系至地心系的坐标转换矩阵。

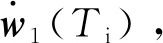
第一步：计算从TB时刻开始的理想惯性平台系下的位置、速度和加速度，计算方程为：

(3)

式中地心惯性系下的重力加速度采用式(4)计算[5]：

(4)

式中：J2=0.001 082 63，a=6 378 140 m,μ=3.986 004 4×1014(m3/s2),X2(Ti)=[xyz],r=(X2(Ti)TX2(Ti))1/2。

采用Runge-Kutta方法起步，采用Adams-PECE方法[6-7]求解式(3)计算得到理想惯性平台系下的导航输出参数。

第二步：由理想惯性平台系下的导航参数计算地心系下的导航参数。设地球旋转角速度为ω，由理想惯性平台系到地心系的位置、速度和加速度参数坐标转换为：

X3(Ti)=Rz(ωTi)(CX1(Ti)+X3(T0))

(5)

(6)

利用式(5)、式(6)对初始参数{B0，L0，H0，β，α，γ}微分，得到对地心系下位置、速度的误差传递公式：

(7)

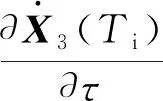
(8)

式中，τ∈{B0，L0，H0，β，α，γ}。

2 初始参数对地心系导航参数影响

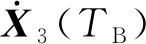
(9)

S是初始参数绝对误差界[S0-L,S0+L]内的向量，d(f(S),f(S0))是关机时刻轨道位置或者速度参数某个分量偏差的欧式距离。

3 算例与分析

3.1 仿真轨道生成和计算逼近精度分析

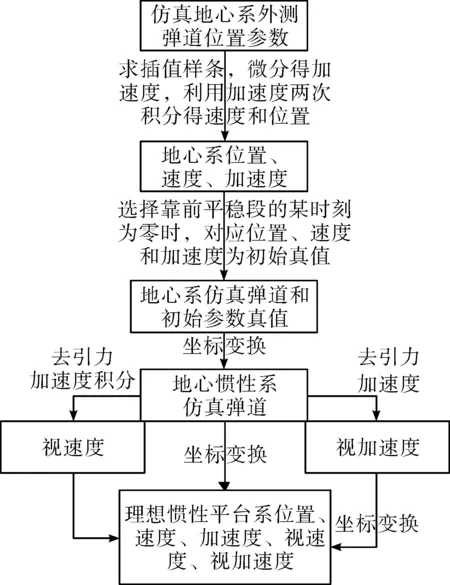
图2 仿真轨道生成示意图

表1 位置和速度逼近精度统计结果

计算中发现两个问题：一个是位置计算会产生误差累积，轨道偏差绝对值最大值都是最后一点，精度满足影响分析要求。这是因为初始速度真值在仿真生成中的舍入误差造成的。用Cowell积分方法直接由加速度积分位置会在仿真中避免速度误差引起的误差累积，但导航方程模型(3)中有直接参加计算的速度测量项，所以不采用Cowell方法。另一个是特征段复杂力学环境下的轨道对导航参数计算的逼近精度会产生影响，如图3所示，理想惯性平台系Y方向80～81 s为特征段，轨道偏差剧烈变化。特征段逼近精度没有参与表1的统计。

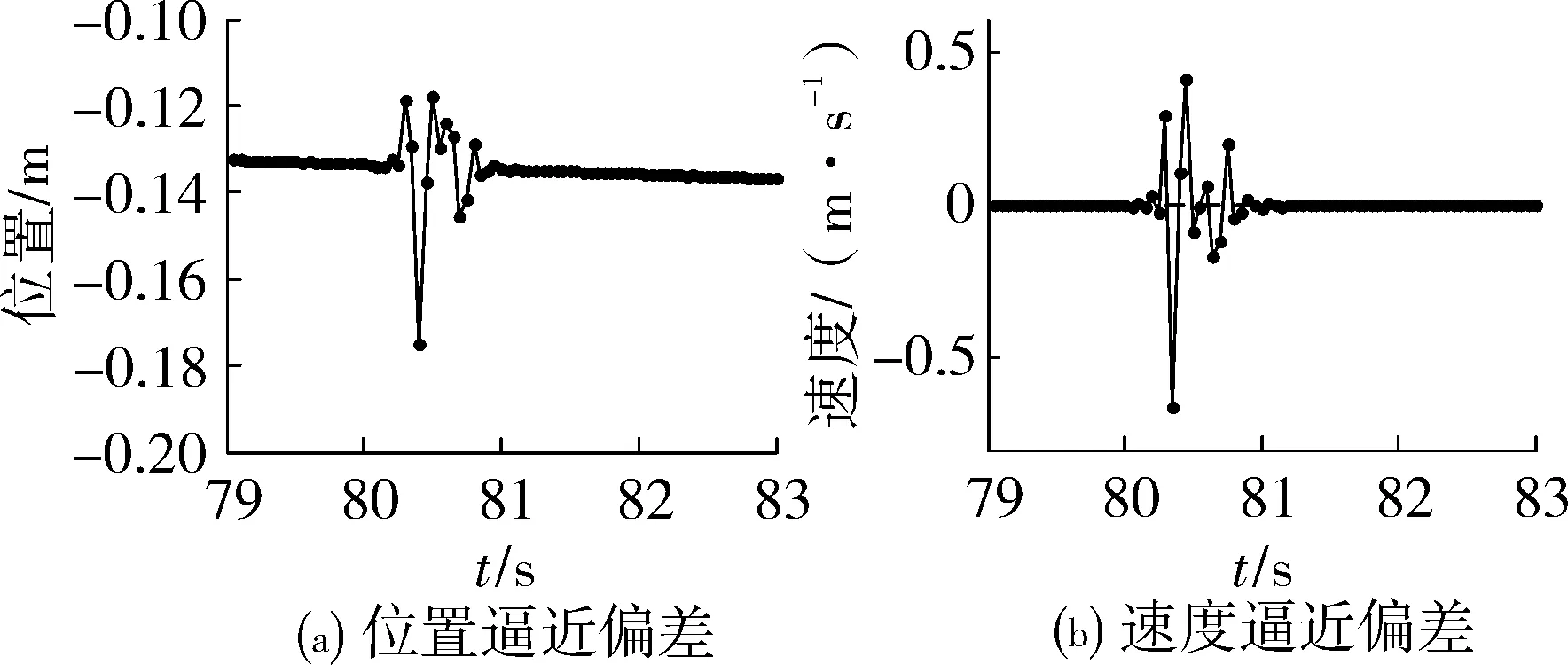
图3 特征段对导航计算逼近精度影响

3.2 初始参数对于导航输出的影响计算

采用3.1节中的仿真轨道，假设飞行器共有3级，做高机动主动段飞行280 s，并且在280 s关机。在不考虑惯性器件误差和安装角偏差条件下，考察由动机座传递给平台，用于导航计算的初始参数误差对平台惯导输出的地心系结果影响。

由于平台惯性导航误差具有累积性，对于给定的初始参数误差，选择关机时刻导航输出参数与真实偏差在3个方向上的和作为初始参数误差对导航输出的影响。单个初始参数误差对关机时刻轨道影响结果如图4～图6所示：图中纵坐标分别为对关机时刻轨道位置和速度的影响，横坐标为初始参数上添加的误差量级；可以看出，关机时刻轨道误差随初始参数误差增加且线性，除了北向速度和东向速度外，不同参数线性斜率不同。北向速度和东向速度对位置和速度参数的影响相同，表现为在图6上重合。计算影响结果与采用式(7)、式(8)的计算结果，对于{B0，L0，H0}符合较好，对于{β，α，γ}差异较大。这是微分模型没有考虑引力加速度项的结果。实际使用时，尽量避免使用微分公式。

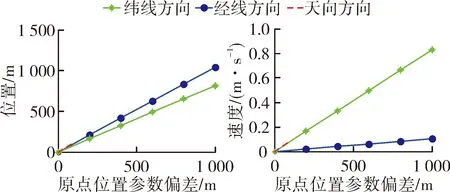
图4 原点位置参数偏差对轨道影响

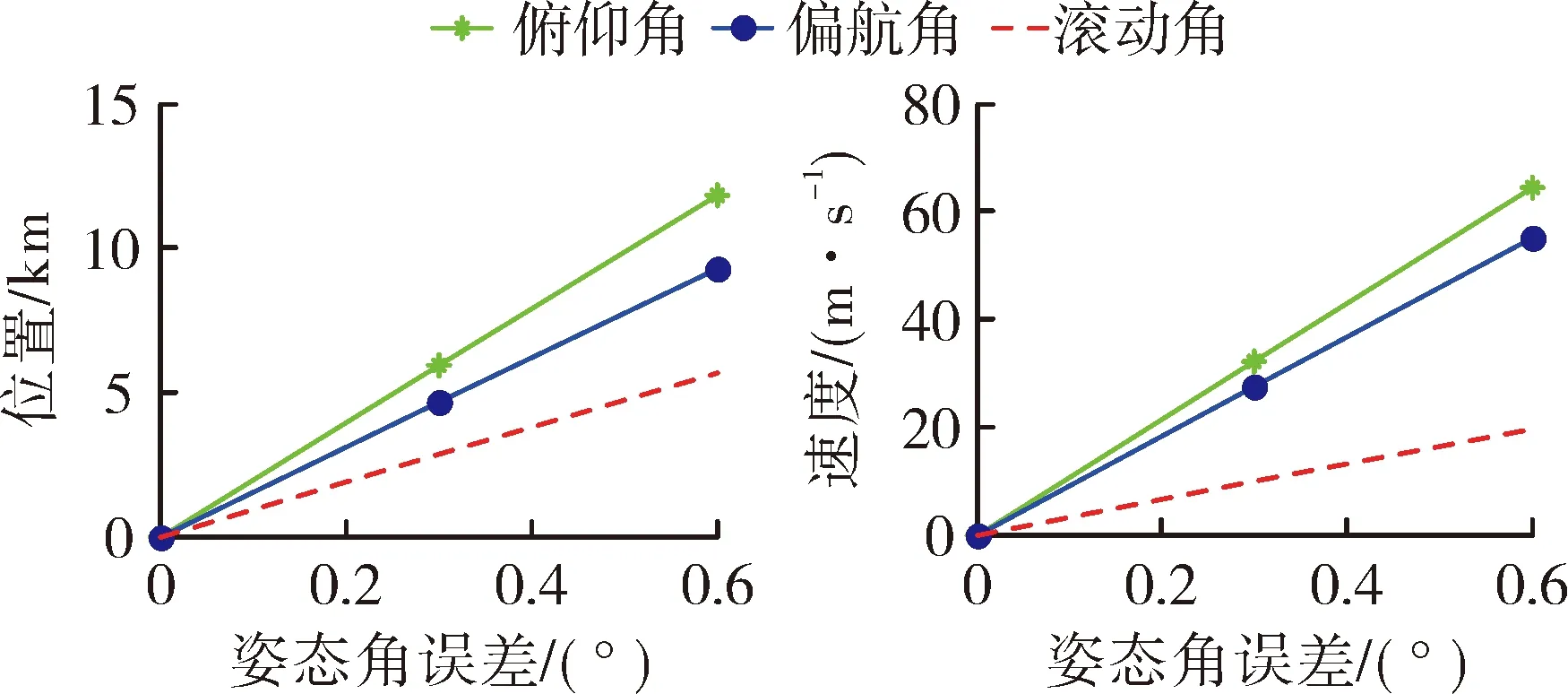
图5 平台姿态角误差对轨道影响

图6 初始速度误差对轨道影响

为考察初始参数对轨道的综合影响，设置某次飞行的初始参数绝对误差界如表2所示，进行4 000次蒙特卡洛仿真计算结果和绝对误差界计算结果如表3所示，其中绝对误差界结果由各个方向的位置和速度单独搜索计算得到。

表2 初始参数绝对误差界

表3 初始参数误差对关机时刻轨道影响

4 结束语

文中针对初始参数对动机座平台式导航参数的影响进行了评估，建立了导航参数计算模型，分别给出了单个初始参数误差对轨道结果的影响和初始参数误差对轨道结果的综合影响评估方法。与惯性器件误差和平台安装角度偏差不同，初始参数误差是由动机座传递给平台的误差，是随着发射环境变化而变化的动态误差。在应用中需要注意，不同发射原点与射向对应的初始参数偏差影响是不同的，需要在载体飞行前根据发射条件进行具体评估。